1 PLANTEAMIENTO DE LA ECUACIÓN DEL TRANSPORTE
RADIATIVO
Hemos visto que el principal mecanismo de
transporte de energía térmica en las atmósferas estelares es el transporte
radiativo. En particular, este mecanismo prevalece en las capas superficiales
de las estrellas más tempranas que F5.
En los objetos más tardíos comienzan a tener importancia los procesos
convectivos y en las estrellas de tipo M la convección predomina. Por el
momento sólo consideraremos el transporte de energía por radiación e
incluiremos más adelante la convección.
Consideremos una porción de materia que emite y absorbe radiación.
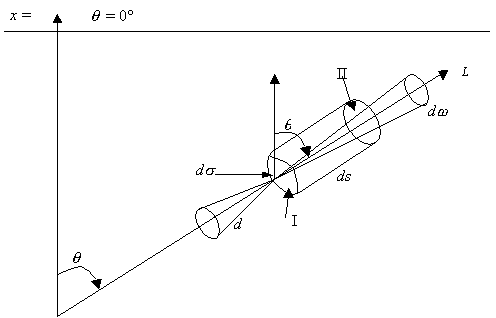
En particular, consideremos un cilindro elemental de altura ds y base ds, tal como el esquematizado en la Figura 7-1. Llamaremos I y II a las dos caras del cilindro. La
energía radiante E(n) de frecuencia comprendida entre (n,n+dn), que incide normalmente a ds sobre la cara I, dentro del
ángulo sólido dw y en
el tiempo dt es :
E(n)i
= In dw ds dn dt, (7.1)
en la cual In es la intensidad específica monocromática en el punto central de
la cara I y en la dirección q.
Figura 7-1 : Representación de
un cilindro elemental de material estelar
La intensidad que emerge normalmente de la cara II será In + dIn, en la cual dIn representa el incremento de la intensidad específica monocromática
debido a los procesos de absorción y emisión que ocurrieron dentro del
cilindro. Este incremento puede en principio ser positivo, negativo o nulo. En
consecuencia, la energía radiante E(n)e de frecuencia comprendida
entre n y (n + dn) que emerge normalmente de la cara II del cilindro elemental,
dentro del ángulo sólido dw y en
el tiempo dt será :
E(n)e = (In + dIn) dw ds dn dt (7.2)
Teniendo en cuenta la expresión (6.51), la cantidad de energía con frecuencias comprendidas entre n y (n + dn), emitida dentro del cilindro en la dirección dw y en el tiempo dt es :
DE(n)em = en dV dw dn dt
Puesto que en = jnr y dV = ds ds , se tiene :
DE(n)em = jnr ds ds dw dn dt (7.3)
Por otra parte, la cantidad de energía absorbida dentro del cilindro elemental puede expresarse de la siguiente manera :
DE(n)abs = - knr E(n)i ds,
la cual es
formalmente idéntica a la expresión (6.45). Reemplazando en la expresión
anterior el valor de E(n)i de (7.1), se obtiene :
DE(n)abs
= -knr In ds dw ds dn dt
(7.4)
Si se admite que la energía que emerge de la cara II del cilindro elemental debe ser igual a la que penetró por la cara I, más la que se creó dentro del cilindro, disminuida por la cantidad que éste absorbió, se tiene :
E(n)e = E(n)i + DE(n)em + DE(n)abs (7.5)
En virtud de las expresiones (7.1), (7.2), (7.3) y (7.4), la igualdad anterior se transforma en la siguiente ecuación diferencial :
![]() ,
(7.6)
,
(7.6)
conocida como ecuación general del transporte
radiativo.
Esta ecuación describe los cambios que sufre la intensidad específica
monocromática a medida que un rayo de intensidad In atraviesa un medio que absorbe y emite con coeficientes kn y jn, respectivamente, siendo r la densidad del medio y ds
la trayectoria elemental seguida por el rayo.