Próxima: Reconstrução Através de Projeções Volta: Transformadas de Fourier Anterior: Gaussiana

Restauração da Imagem

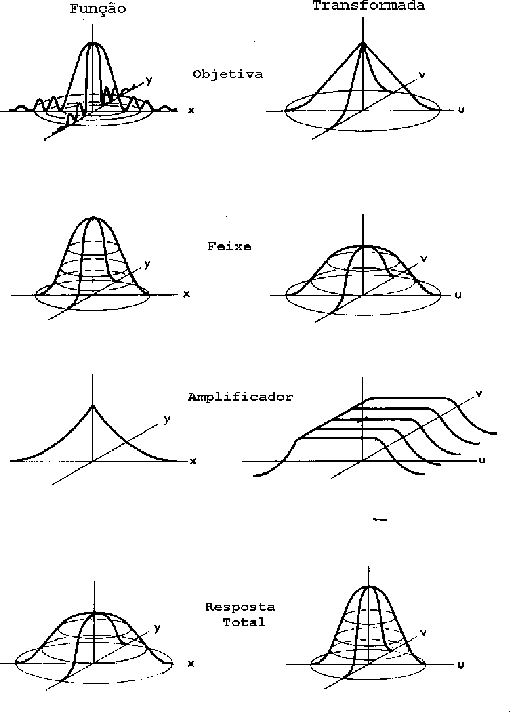
A restauração da imagem consiste na remoção ou redução da degradação da imagem ocorrida durante a aquisição, incluindo o borramento introduzido pelo sistema óptico, movimento da imagem, bem como o ruído eletrônico e fotométrico. Em um sistema linear, a degradação da imagem pode ser modelada por uma função de espalhamento de ponto (Point Spread Function - PSF), ou impulso resposta, e pelo ruído, que é aditivo.

A forma mais simples de restaurar uma imagem é utilizando o filtro inverso, onde a função degradação é invertida, e utilizada para restaurar a imagem.

Uma imagem ideal $f_I(x,y)$ passa por um sistema linear de degradação com um impulso resposta $h_D(x,y)$, sofrendo ainda a adição de um ruído não correlacionado $r(x,y)$. A imagem observada, $f_O(x,y)$ é portanto a imagem ideal, convoluída com a PSF $h_D(x,y)$, mais o ruído:

$$f_O(x,y) = \int_{-\infty}^\infty \int_{-\infty}^\infty f_I(x,y) h_D(x-\alpha,y-\beta)d\alpha\,d\beta + r(x,y).$$

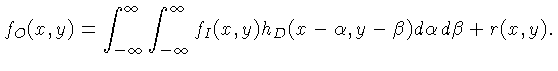
A restauração da imagem será dada pela convolução com o filtro inverso, $h_R(x,y)$:

$$\hat{f}_I(x,y) = \left[ f_I(x,y)*h_D(x,y)+r(x,y)\right]*h_R(x,y).$$

Note que a imagem restaurada 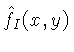$\hat{f}_I(x,y)$ não é idêntica à imagem ideal, devido a presença do ruído.

Podemos utilizar o Teorema da Convolução para trabalhar no domínio de Fourier:

$$\hat{F}_I\left(w_x,w_y)\right) = \left[F_I\left(w_x,w_y\right) H_D\left(w_x,w_y\right) + R\left(w_x,w_y\right)\right] H_R\left(w_x,w_y\right),$$

onde $F_I\left(w_x,w_y\right)$ representa a transformada de Fourier da imagem $f_I(x,y)$, ... Se o filtro de restauração $H_R\left(w_x,w_y\right)$, que é a transformada de Fourier da função restauração $h_R(x,y)$ for dado por:

$$H_R\left(w_x,w_y\right) = \frac{1}{H_D\left(w_x,w_y\right)},$$

a transformada de Fourier da imagem reconstruída será dada por:

$$\hat{F}_I\left(w_x,w_y\right) = F_I\left(w_x,w_y\right) + \frac{R\left(w_x,w_y\right)}{H_D\left(w_x,w_y\right)},$$

e a função restaurada pode ser escrita como:

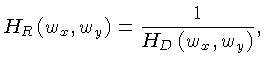
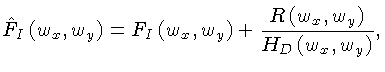
$$\hat{f}_I(x,y) = f_I(x,y) + \frac{1}{4\pi^2} \int_{-\infty}^\inft... ...)}{H_D\left(w_x,w_y\right)} \exp\left[i\left(w_xx+w_yy\right)\right]dw_x\,dw_y.$$

Na ausência de ruído, a restauração seria perfeita. Entretanto, o erro de restauração se torna grande para as frequências espaciais onde a degradação $H_D\left(w_x,w_y\right)$ é pequena. Tipicamente, tanto $H_D\left(w_x,w_y\right)$ quanto $F_I\left(w_x,w_y\right)$ são pequenas em altas frequências, e portanto a estrutura espacial detalhada é altamente degradada.

Em 1967, C.W. Helstrom publicou no Journal of the Optical Society of America o artigo intitulado Image Restoration by the Method of Least Squares, calculando o filtro que minimiza o desvio padrão médio, pelo método dos mínimos quadrados:

$$\sigma^2 = \left[f_I(x,y)-\hat{f}_I(x,y)\right]^2,$$

assumindo que a transformada de Fourier do ruído médio $r(x,y)$ é conhecida, e dada por:

$$R\left(w_x,w_y\right) = {\cal{F}}\left[r\left(x,y\right)\right].$$

Neste caso, o filtro de deconvolução de Wiener é dado por:

$$H_R\left(w_x,w_y\right) = \frac{H_D^*\left(w_x,w_y\right)}{\left\vert H_D\left(w_x,w_y\right)\right\vert^2+R\left(w_x,w_y\right)},$$ (4.16)

onde $H_D^*\left(w_x,w_y\right)$ é o complexo conjugado de $H_D\left(w_x,w_y\right)$, o filtro de degradação espacial. O espectro de potência do ruído torna o filtro suave e não singular mesmo na região de alta frequência. Embora seja optimizada, a deconvolução de Wiener assume que o ruído é uniforme e estacionário, quando na verdade o ruído muitas vezes depende do sinal e portanto não é espacialmente não correlacionado. Estes efeitos devem ser levados em conta na determinação da transformada de Fourier do ruído, e na escolha da região de cálculo.

Próxima: Reconstrução Através de Projeções Volta: Transformadas de Fourier Anterior: Gaussiana