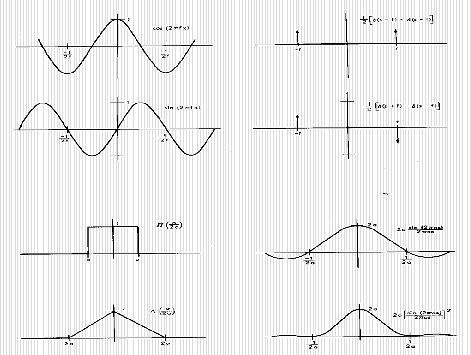
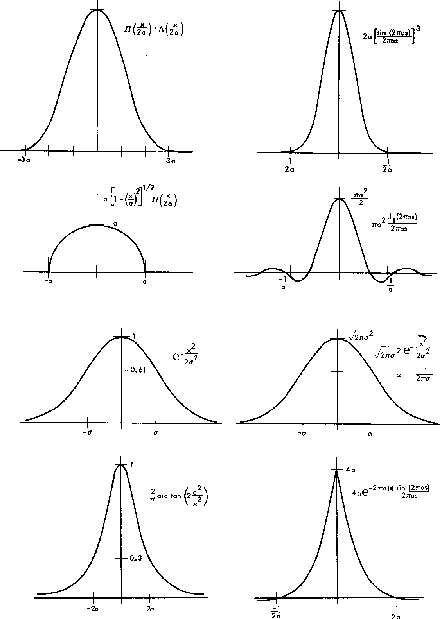
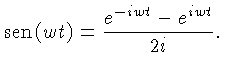Próxima: Transformada Bi-dimensionais Volta: Fundamentos de Radiodiagnóstico por Imagem Anterior: Histograma

Transformadas de Fourier

Em ultrasom, um sinal Doppler consiste na superposição de ondas de frequências diferentes, correspondentes por exemplo a diferentes velocidades do sangue. Em um sinal de ressonância nuclear magnética, o sinal de radio frequência também consiste de diferentes frequências e fases, que podem ser analisados diretamente por um espectro de frequências, ou Transformada de Fourier [desenvolvida por Jean Fourier (1768-1830) em 1822].

$\epsfig{file=Fourier.epsf,width=5cm,clip=}$

Entretanto, a transformada pode ser utilizada também na reconstrução bi-dimensional de imagens em geral, por sua facilidade e rapidez de cálculo, comparado com a resolução das equações de projeção algebricamente, que consistem na montagem de uma matriz e sua resolução.

Um ponto importante da transformada, é o critério de Nyquist, que especifica que um sinal precisa ser amostrado pelo menos duas vezes em cada ciclo de variação, isto é, a frequência de amostragem (frequência de Nyquist) precisa ser no mínimo o dobro da maior frequência presente no sinal. Se não for observado o critério, os sinais de mais alta frequência serão erroneamente registrados como de baixa frequência, fenômeno chamado de alias (como a impressão da roda girando no sentido inverso que vemos na televisão). Por exemplo, em imageamento Doppler, onde o fluxo do sangue é medido por uma série de pulsos ultrasônicos, se os pulsos não forem repetidos com rapidez suficiente, um fluxo rápido em uma direção pode ser interpretado como um fluxo lento na direção oposta.

A transformada de Fourier de uma função f(x) é definida como:

${\cal{F}}[f(x)] \equiv F(w_x) = \int_{-\infty}^\infty f(x) e^{-2i\pi w_xx} dx$

(4.1)

e a transformada inversa, que recupera a função original é definida como:

${\cal{F}}^{-1}[F(w_x)] \equiv f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty F(w_x) e^{2i\pi w_xx} dw_x$

(4.2)

onde

é a frequência angular, e $i\equiv \sqrt{-1}$ .

Para cada frequência , integramos a função sobre todos os valores da coordenada . Se o valor da integral for grande para esta frequência, então o sinal tem uma componente significativa nesta frequência, isto é, uma parte significativa deste sinal é composto por esta frequência.

Podemos também definir:

$\displaystyle \boxed{{\cal{F}}[f(x)] \equiv F(\nu) = \int_{-\infty}^\infty f(x) e^{-i \nu x} dx,}$

(4.3)

e a transformada inversa, que recupera a função original é definida como :

$\displaystyle \boxed{{\cal{F}}^{-1}[F(\nu)] \equiv f(x) = \frac{1}{2\pi}\int_{-\infty}^\infty F(\nu) e^{i\nu x} d\nu,}$

(4.4)

onde $\nu=2\pi w_x$ é a frequência linear.

Note que:

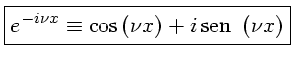
$e^{-i\nu x} \equiv cos(\nu x) + i sen(\nu x)$

A condição suficiente para e existência da transformada de Fourier de uma função qualquer é que a função seja integrável, e finita, isto é:

$\displaystyle \int_{-\infty}^\infty \vert f(x)\vert dx < \infty$

(4.5)

As imagens que estamos interessados são sempre integráveis e finitas.

$\epsfig{file=ft.epsf,width=10cm,clip=}$

Embora a imagem seja real, a transformada de Fourier é uma função complexa, com coeficientes reais e imaginários:

$\displaystyle \boxed{F(w_x) = \Re[F(w_x)] + i\Im[F(w_x)].}$

O espectro de potências é definido como:

$\displaystyle \boxed{P(w_x) = \Re[F(w_x)]^2 + \Im[F(w_x)]^2,}$

e o ângulo de fase é dado por:

$\displaystyle \boxed{\phi(w_x)=\tan^{-1} \frac {\Im[F(w_x)]}{\Re[F(w_x)]}.}$

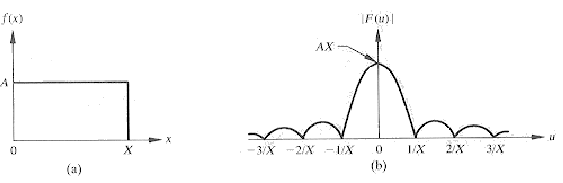
Por exemplo, podemos calcular a transformada de Fourier de um pulso retangular, definido por:

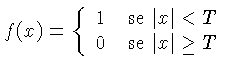
$\displaystyle f(x) = \left\{ \begin{array}{ll} 1&\mbox{se $\vert x\vert<T$}\\ 0&\mbox{se $\vert x\vert\geq T$} \end{array}\right.$

A transformada de Fourier

é dada por:

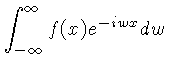$\displaystyle {\cal{F}}[f(x)] \equiv F(w)$	$\displaystyle =$	$\displaystyle \int_{-\infty}^\infty f(x) e^{-iwx} dw$
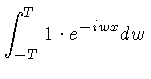	$\displaystyle =$	$\displaystyle \int_{-T}^T 1\cdot e^{-iwx} dw$
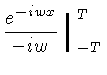	$\displaystyle =$	$\displaystyle \frac{e^{-iwx}}{-iw} \Big\bracevert_{-T}^T$
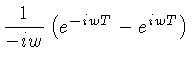	$\displaystyle =$	$\displaystyle \frac{1}{-iw}\left(e^{-iwT}-e^{iwT}\right)$
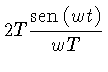	$\displaystyle =$	$\displaystyle 2T \frac{\mathrm{sen}\,(wt)}{wT}$
	$\displaystyle =$	$\displaystyle 2T \mathrm{sinc}\,(wT),$