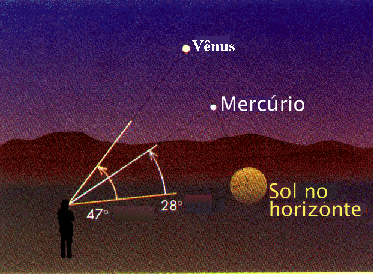
Copérnico determinou as distâncias dentro do sistema solar em termos da distância Terra-Sol, ou seja, em unidades astronômicas (UA).
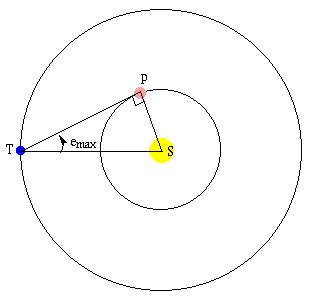
Quando o planeta inferior está em
máxima elongação (
),
o ângulo entre Terra e Sol, na posição do planeta, será 90°.
Então nessa situação Sol, Terra e planeta formam um triângulo
retângulo, e a distância do planeta ao Sol será:
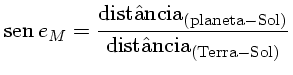
No caso de Mercúrio:
distância (Sol-Mercúrio)=sen 28° × 1 UA = 0,46 UA.
Devido à alta excentricidade da órbita de Mercúrio (0,206),
a elongação máxima varia de 18° a 28°, e
a distância de 0,39 a 0,46 UA.
Mercúrio atinge máxima elongação leste (visível ao entardecer) em 16 de novembro de 2024 (23° do Sol), em Virgem, com magnitude -1,17. Mercúrio atinge máxima elongação oeste (visível ao amanhecer) em 25 de dezembro de 2024. Em 5 de dezembro de 2024, Mercúrio está em conjunção solar inferior, isto é, entre o Sol e a Terra.
Em 4 de junho de 2023, Vênus atingiu elongação máxima a leste 45,4°, visível durante o entardecer. Em 6 de outubro de 2024, Vênus está visível ao entardecer, em Porto Alegre até as 21:02, com magnitude -3,93, na constelação de Libra. Em 10 de janeiro de 2025, Vênus estará em elongação máxima leste, visível ao entardecer, com magnitude -4,4, 51% da face iluminada e diâmetro aparente de 24,5 segundos de arco. Em 4 de junho de 2024, Vênus esteve em conjunção solar superior, atrás do Sol. Em 23 de março de 2025, Vênus estará em conjunção solar inferior, entre o Sol e a Terra. Em 31 de maio de 2025 Vênus estará em máxima elongação oeste, 48°, visível ao amanhecer, com 50% da face iluminada. Em Porto Alegre estará 42° acima do horizonte ao amanhecer no dia 22 de maio de 2025, com 44% da face iluminada. Em 14 de agosto de 2026 Vênus estará na máxima elongação leste. Em 3 de janeiro de 2027 Vênus estará na máxima elongação oeste.
Observando Marte, Copérnico viu que o intervalo de tempo decorrido entre uma oposição e uma quadratura é de 106 dias.
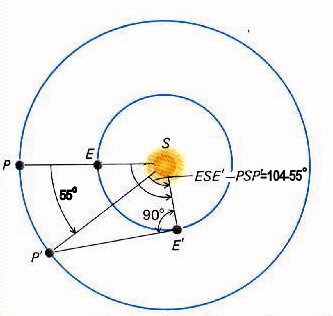Nesse período de 106 dias, a Terra percorre uma aproximadamente distância angular de
ESE'=104° (pois se em 365,25 dias ela percorre 360°, em
106 dias ela percorre 106/365,25 × 360°).
Como o período sideral de Marte é de 687 dias, então a distância angular percorrida por Marte nesse mesmo período de 106 dias será: PSP'=55° = 106/687 x 360°.
Agora, considerando o triângulo formado pelo Sol (S), Terra (E') e Marte (P') na quadratura (SE'P' na figura), o ângulo entre o Sol e o planeta, visto da Terra, é 90°, e o ângulo entre Terra e Marte, visto do Sol, é ESE'-PSP'=104° - 55 °= 49°.
Então a distância entre Marte e Sol é:
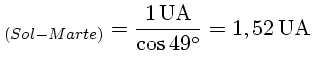
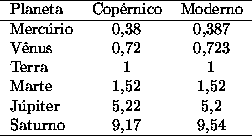
A tabela abaixo mostra uma comparação entre os valores das distâncias
dos planetas ao Sol, em unidades astronômicas, determinadas por Copérnico, assumindo órbitas circulares,
e os valores atuais.
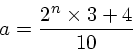
| Planeta | n | Lei de Titius-Bode | Semi-Eixo Maior |
| Mercúrio |  | 0,40 | 0,39 |
| Vênus | 0 | 0,70 | 0,72 |
| Terra | 1 | 1,00 | 1,00 |
| Marte | 2 | 1,60 | 1,52 |
| Cinturão de Asteróides | 3 | 2,80 | 2,8 |
| Júpiter | 4 | 5,20 | 5,20 |
| Saturno | 5 | 10,0 | 9,54 |
| Urano | 6 | 19,6 | 19,2 |
| Netuno | - | - | 30,1 |
| Plutão | 7 | 38,8 | 39,4 |
Movimento dos Planetas
