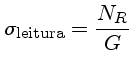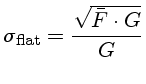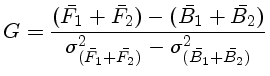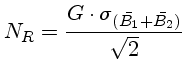Ruído de uma imagem
Precisamos primeiro distinguir precisão,
devido às incertezas randômicas, que altera a sua repetibilidade,
e acurácia, afetada por incertezas sistemáticas,
que indica o quanto a medida se aproxima do valor real.
As incertezas randômicas
podem ser reduzidas com maior número de medidas, mas as incertezas
sistemáticas, só com calibração.
Friedrich
Wilhelm Bessel (1784-1846), o pai da astrometria moderna, foi o primeiro astrônomo a considerar que antes de poder usar uma medida,
ele precisava determinar todos os tipos de incertezas que pudessem afetar a medida.
Nenhuma medida tem significado se não for acompanhada da estimativa de sua incerteza. Note que a estimativa das incertezas pode afetar o próprio valor. Por exemplo, se usarmos várias medidas de calibração, e encontrarmos que uma medida tem uma incerteza muito grande, excluindo-a alteramos diretamente o valor da medida e não somente a estimativa de sua incerteza.
No ótico, medimos em geral o número de fótons, pois cada fóton produz
um elétron no detector, mas no raio-X, devido a alta energia dos fótons,
até milhares de elétrons são produzidos por cada fóton.
Entretanto o que medimos não é diretamente o fluxo do objeto, já que o
fluxo observado depende da área do coletor, perdas e ganhos entre a
fonte e o instrumento, incluindo a atmosfera da Terra, e a eficiência
do coletor e detector.
A contagem observada pode ser escrita como
onde 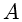 é a área coletora,
é a área coletora, 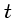 o tempo de integração,
Fλ, o fluxo,
é a energia por unidade de área e unidade de tempo,
hc/λ a energia de cada fóton,
o tempo de integração,
Fλ, o fluxo,
é a energia por unidade de área e unidade de tempo,
hc/λ a energia de cada fóton,
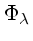 a eficiência do sistema, e
a eficiência do sistema, e
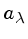 a transmissão atmosférica.
a transmissão atmosférica.
Para uma taxa de fótons emitidos, existe uma distribuição de probabilidades
que nos dá o número de fótons que detectamos, mesmo se a eficiência de
detecção for de 100%.
Vamos definir como 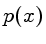 a probabilidade de um evento ocorrer entre
a probabilidade de um evento ocorrer entre
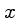 e
e 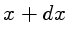 :
:
a média 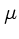 :
a variança
:
a variança 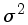 :
o desvio padrão
:
o desvio padrão 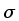 , e o
modo, que é o valor mais provável da distribuição,
Precisamos também definir a média do conjunto de medidas,
, e o
modo, que é o valor mais provável da distribuição,
Precisamos também definir a média do conjunto de medidas, 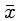 :
e a variança do conjunto:
Como nossas medidas são finitas, a média do conjunto de medidas
:
e a variança do conjunto:
Como nossas medidas são finitas, a média do conjunto de medidas 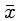 não é idêntica à média μ.
não é idêntica à média μ.
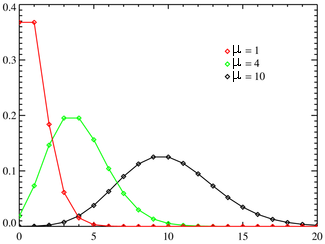
A distribuição de fótons p, para um grande número de fótons
de média 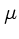 é dada pela
distribuição
de Poisson, descrita por
Siméon-Denis Poisson (1781-1840), como uma
extensão da distribuição binomial - válida quando só há duas soluções
possíveis.
A distribuição de Poisson,
P, é válida quando a probabilidade de
sucesso de cada evento é baixa e o número de tentativas muito grande,
é dada pela
distribuição
de Poisson, descrita por
Siméon-Denis Poisson (1781-1840), como uma
extensão da distribuição binomial - válida quando só há duas soluções
possíveis.
A distribuição de Poisson,
P, é válida quando a probabilidade de
sucesso de cada evento é baixa e o número de tentativas muito grande,
e a
variança é dada por
com 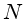 o número total de fótons emitidos e
o número total de fótons emitidos e 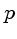 a
probabilidade de detectarmos um fóton durante a observação.
A distribuição de Poisson tem esta interessante propriedade,
a média é igual à variança: μ=σ2=N.
Logo, se detectamos
a
probabilidade de detectarmos um fóton durante a observação.
A distribuição de Poisson tem esta interessante propriedade,
a média é igual à variança: μ=σ2=N.
Logo, se detectamos 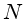 fótons, o desvio padrão é
fótons, o desvio padrão é
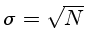 .
.
A equação do CCD
descreve as contribuições dos diversos tipos
de ruído nas medidas. Suponhamos que tenhamos 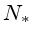 fotoelétrons (contagens)
detectados de um objeto. O ruído estatístico (Poissoniano) da
medida será dado por
fotoelétrons (contagens)
detectados de um objeto. O ruído estatístico (Poissoniano) da
medida será dado por
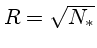 .
Mas em um CCD temos outras fontes de ruído:
.
Mas em um CCD temos outras fontes de ruído:
onde
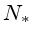 |
número total de contagens coletadas do objeto (em elétrons) |
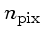 |
número de píxeis considerados |
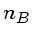 |
número de píxeis de fundo (céu) |
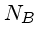 |
número total de contagens por pixel de fundo (céu, em elétrons) |
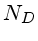 |
número total de contagens por pixel de corrente de escuro (térmicos,
em elétrons) |
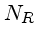 |
ruído de leitura por pixel (em elétrons) |
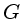 |
Ganho do detector (número de elétrons/ADU) |
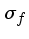 |
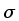 da contagem fracional perdida na discretização por pixel (em ADU) da contagem fracional perdida na discretização por pixel (em ADU) |
As fontes de ruído são:
- Ruido randomico, devido a natureza discreta da luz e da carga elétrica
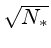 .
O termo (1+npix/nB) é uma medida da incerteza causada
por erros introduzidos na estimativa do fundo (background).
Quanto maior o número de píxeis usados na estimativa do fundo, menor a
incerteza na sua medida, mas é preciso determinar se não há variação
real no fundo, causados por exemplo pela variação do céu devido a Lua,
ou luz espalhada.
Uma estimativa do fundo é o valor mais frequente na distribuição de valores
em um anel em torno do objeto. Um refinamento é recalcular o valor após
eliminar valores ± 3× o desvio padrão.
.
O termo (1+npix/nB) é uma medida da incerteza causada
por erros introduzidos na estimativa do fundo (background).
Quanto maior o número de píxeis usados na estimativa do fundo, menor a
incerteza na sua medida, mas é preciso determinar se não há variação
real no fundo, causados por exemplo pela variação do céu devido a Lua,
ou luz espalhada.
Uma estimativa do fundo é o valor mais frequente na distribuição de valores
em um anel em torno do objeto. Um refinamento é recalcular o valor após
eliminar valores ± 3× o desvio padrão.
- Ruido de leitura, devido ao amplificador e à própria câmara:
tem duas partes, a térmica, devido ao movimento
térmico dos átomos, e a flutuação rápida (flicker, A~1/f), que depende fortemente da
freqüência (f) de leitura, se origina na existência de estados de vida longa (traps)
na interface silício-óxido.
A alteração de potenciais para a leitura
(clocking) também pode introduzir cargas espúrias.
Em algumas câmaras, podemos reduzir o ruído de leitura reduzindo a velocidade
de leitura. Por exemplo, velocidades de leitura de 50 μs/pixel
são alcançaveis, mas para manter ruído de leitura menor que 10 e,
velocidades de 20 μs/pixel são mais comuns, mas isto implica
em 200 s para ler um CCD de 2048×2048.
Binando o CCD, pode-se ter um menor ruído de leitura por pixel efetivo,
menor tempo de leitura, mas com menor resolução.
Por exemplo, no Soar Optical Imager,
Ruído de leitura: 3,1 elétrons no modo de leitura lento, 4,4 elétrons no modo rápido.
Corrente de escuro: ≈2 e/hr
Tempo de leitura: Binning Leitura lenta Leitura Rápida
1×1 106.0 s 20.6 s
2×2 31.7 s 10.9 s
4×4 - 6.1 s
Ganho 0.4 e/ADU (leitura lenta) ou 2.0 e/ADU (leitura rápida)
Eficiência de transferência de carga: 99.9995
- Corrente de escuro: mesmo na ausência de luz, pares elétrons-buracos se
formam dentro do sensor, geralmente com uma dependência exponencial da temperatura.
Eles também obedecem à estatística Poissoniana,
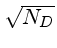 . Podemos
subtrair a corrente de escuro média, mas não o ruído associado.
A corrente de escuro depende da temperatura e do tempo de integração.
. Podemos
subtrair a corrente de escuro média, mas não o ruído associado.
A corrente de escuro depende da temperatura e do tempo de integração.
- Erros devido à discretizacão:
O ganho de um CCD é um parâmetro que se pode alterar na eletrônica de saída,
e determina quantos elétrons coletados em cada pixel são necessários para cada contagem na imagem (ADU).
Note que a definição de ganho não é a óbvia: quanto maior o ganho, maior
o número de elétrons necessários para uma contagem (e/ADU), isto é, menor a contagem final.
Uma das grandes vantagens de um CCD é que eles têm uma resposta linear (número de contagens diretamente proporcional ao número de elétrons coletados em cada pixel) em uma grande faixa de valores.
Mas o maior número de saída que um CCD pode produzir é determinado pelo número de bits no conversor analógico-digital.
Por exemplo, um A/D de 15 bits pode contar entre 0 e 32 767 ADUs (2n-1).
Para contar uma capacidade de poço total de 150 000 elétrons, o ganho precisa ser 4.5. Para o CCD mostrado na figura de linearidade, a não-linearidade começa a ser importante para uma entrada de 1,17×105 fótons (26 000 ADU), ainda dentro da faixa de capacidade do A/D.
É necessário cuidar para que não ocorra saturação do conversor A/D, saturação
da capacidade total de poço, e não-linearidade. No nosso exemplo,
a não-linearidade em 26 000 ADU ocorre primeiro,
e não é facilmente detectável, pois não causa
vazamento (bleeding)
ou máximos planos (flat tops), mas altera as contagens dos objetos
mais brilhantes.
Uma maneira de se obter a curva de linearidade, é observar um campo com objetos fracos e brilhantes, e obter-se imagens com tempos de exposição digamos de 1, 2, 4, 8 e 16 s.
Gráficos das contagens das estrelas versus diferentes exposições fornecerá a curva de linearidade.
Mas sempre leve em conta que quanto maior o ganho, maior o erro de digitalização, pois só números inteiros de ADU são registrados, desprezando as partes fracionais, o que pode ser dominante nas partes mais extensas e de menor brilho, pois teremos um ruído de digitalização para cada pixel contribuindo para a imagem.
O ganho do detector introduz
uma incerteza (G/2 e) e
a contagem fracional perdida na digitalização também introduz erro de
quantização. Por exemplo, se o ganho for igual a 4, são necessários
4 elétrons por cada contagem. As frações são desprezadas.
O número de bits do conversor analógico-digital (A/D converter)
em geral não permite a contagem de toda a capacidade de poço
do CCD. Conversores com menor número de bits trabalham mais rápido.
Conversores de 16 bits (máxima contagem
216=65536) são comuns,
e de 18 bits (218=262144) começam a ser disponíveis, mesmo convertendo
a uma velocidade de 1 MHz.
A capacidade de poço depende do tamanho físico do pixel (area ×
profundidade). Um CCD SITe com píxeis de
24 μm chega a 350 mil
elétrons de capacidade de poço e existem CCDs com capacidade de 106
elétrons por pixel. Para ler a capacidade total de poço,
é necessário usar um ganho adequado para o número de bits do
conversor A/D.
- Erros devido à subtração da imagem de escuro. Leva em conta não
só o ruído randomico nas contagens, mas também o ruído de leitura
do CCD.
- Erros devido ao campo plano (flat field). Para corrigir as
variações de ganho dos diversos píxeis contribuindo para a
imagem do objeto, precisamos corrigir pelo flat field, e precisamos levar
em conta a incerteza fracional do flat field.


Flats de cúpula e de céu para o filtro B no Soar Optical Imager.
As
rosquinhas são causadas por grãos de poeira na janela
do CCD, e as variações de intensidade principalmente causadas
pelo processo físico de cortar o ccd para torná-lo fino,
permitindo a exposição à luz pelo lado de trás,
tornando-o sensível no azul.
Cada um dos dois CCD conta com dois ADCs, de sensibilidade diferentes, que causam as variações em quatro partes.

Flats de céu para o filtro U no Soar Optical Imager.
É importante sempre levar em conta a linearidade das contagens na
exposição do flat field, isto é, sempre expor os flats de forma
que as contagens estejam dentro do limite de 1% de não linearidade,
o que em geral ocorre aproximadamente em 60% da capacidade de poço
do CCD.
Precisamos levar em conta que a resposta de cada pixel varia com o comprimento de onda, de modo que precisamos determinar flat fields para cada filtro. Como as lâmpadas de filamentos em geral têm pouca resposta no azul, é necessário usar
lâmpadas de quartzo para determinar a sensibilidade no azul e para espectroscopia. A prática tem mostrado que flat fields compostos da média de muitas exposições são em geral mais precisos que as médias de cada dia. Para minimizar problemas de iluminação, flats de céu são mais precisos, mas precisamos cuidar para que obtê-los logo após o pôr-do-sol ou logo antes do nascer do sol, para evitar contaminação por estrelas, mas cuidando a saturação e não linearidade.
- Bias (viés) ou zero: é uma contagem constante (pedestal)
mesmo em píxeis
não expostos à luz (diafragma fechado),
usada para que não hajam contagens negativas.
Pode ser medido por colunas de overscan (colunas virtuais
produzidas por clocking adicionais) ou
por exposições com tempo de exposição nulos. Se usamos
somente
as colunas de overscan, podemos introduzir ruído se os píxeis
tiverem variações (estruturas) bidimensionais neste valor.
Por isto o recomendado é utilizar os dois, overscan e bias.
O bias, que pode ser de milhares de elétrons, não sofre de ruído
poissônico.
Se fizermos a média sobre
n imagens de bias, cada uma com um
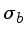 ,
causado por ruído eletrônico,
a incerteza sobre a
média será dada por
,
causado por ruído eletrônico,
a incerteza sobre a
média será dada por
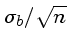 .
.
- Raios cósmicos: são contagens devido tanto ao impacto
de raios cósmicos reais, quanto de decaimento radiativo dentro do
próprio CCD. Podem ser eliminados com a aquisição
de várias imagens, rejeitando os píxeis que se desviam muito
acima de 3 σ,
mesmo nas exposições de bias.
- Não-linearidades: embora os CCDs sejam artefatos com boa
linearidade, ela não é perfeita, isto é, o número de contagens
não é exatamente proporcional ao número de fótons incidentes,
principalmente para altas contagens.
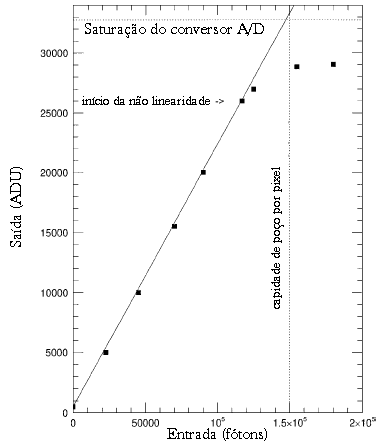
Curva de linearidade para um CCD com pedestal de 500 ADU,
conversor A/D de 15 bits, e capacidade de poço de 150 000 fótons.
A pendente da reta nos dá o ganho usado.
- Franjas de interferência: se o comprimente de onda da luz incidente for
da mesma ordem que a espessura do CCD,
ou interferências pela reflexão de luz quase monocromática dentro do CCD,
ocorrem franjas de interferência,
que
normalmente têm a mesma forma mas com amplitude proporcional à
intensidade da luz incidente.
- Propagação de erros
devido às subtrações
de pedestal (bias) e corrente de escuro, e divisão pelo flat field.
Seja N=N*,
o número de foto-elétrons incidentes multiplicado pela
eficiência quântica do sensor, isto é, o número de
foto-elétrons detectados,
ND o
número de elétrons térmicos gerados.
Note que uma exposição de zero tempo de integração contem somente ruído de leitura.
Nossa derivação é em elétrons, pois estes seguem uma distribuição poissoniana. As contagens expressas em unidades analógico-digitais
(ADU) precisam
ser multiplicadas pelo ganho (G) para transformar em elétrons.
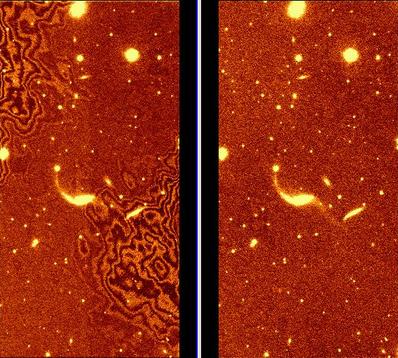
Seja 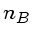 o número de píxeis da região
(anel) de fundo (background), e
o número de píxeis da região
(anel) de fundo (background), e
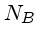 o valor médio do fundo por pixel.
O ruído total sobre as
contagens do objeto após a subtração do fundo
será então
o valor médio do fundo por pixel.
O ruído total sobre as
contagens do objeto após a subtração do fundo
será então
com
Na subtração de corrente de escuro, a incerteza em elétrons na
imagem de escuro é dada por:
A incerteza na imagem (I-D) após a subtração da corrente de escuro,
por propagação de erros, é dada por:
A propagação de erros pela divisão pelo flat, normalizado, desprezando os termos de ordem mais alta, é dada por:
onde
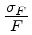 é a razão R/S do flat.
é a razão R/S do flat.
- Erros de transformação: se tivermos que transformar as
contagens para um sistema padrão, ainda precisamos incluir as
incertezas nas transformações, que levam em conta
as incertezas nas padrões, e de cintilação da atmosfera.
onde
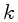 é o coeficiente de extinção naquela banda,
é o coeficiente de extinção naquela banda, 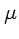 a massa de ar,
a massa de ar,
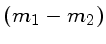 um índice de cor que corrija a variação da banda
passante observada
para a banda fotométrica do sistema padrão, e
um índice de cor que corrija a variação da banda
passante observada
para a banda fotométrica do sistema padrão, e 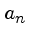 os coeficientes de
transformação.
os coeficientes de
transformação.
- Efeitos cosméticos no CCD: píxeis ruins, píxeis quentes, colunas mortas e bits congelados podem causar problemas na calibração e análise das imagens.
Eles podem ser tratados, mas não corrigidos, por máscaras de píxeis ruins
(bad pixel masks).
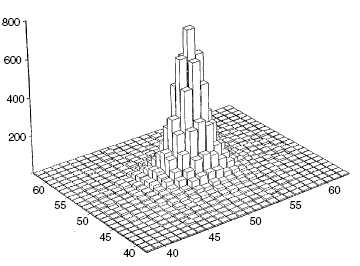
- Erros de contagem no objeto: podemos estimar a contagem sobre o
objeto com fotometria de abertura, ou por fitagem de perfis, chamados
de função de espalhamento pontual (point-spread function - PSF).
Teoricamente a razão sinal/ruído ótima é obtida com uma fitagem de perfil
em que cada píxel tem peso proporcional à intensidade prevista do píxel.
As PSF normalmente usadas são, gaussiana:
lorentziana:
e Moffat:
onde r
é a distância ao centro do objeto e a e b
são parâmetros
de fitagem (Peter B. Stetson, Linsey E. Davis & Dennis R. Crabtree 1990,
Astronomical Society of the Pacific Conference Series,
8, ed. George H. Jacoby, p. 289).
Ainda é possível usar
uma matrix empírica para fitar completamente os dados.
Estas funções podem facilmente ser generalizadas para duas dimensões, para levar em conta erros de acompanhamento do telescópio e aberrações nas imagens.
Para campos densos, em que as imagens dos objetos se sobrepõem, a fitagem da função de espalhamento pontual pode ser a única maneira de realizar as medidas.
Se o objeto for brilhante, a razão sinal-ruído é totalmente dominada pela incerteza na contagem de fótons:
onde n é o número de fótons por segundo do objeto.
Se o ruído de fundo for similar ao ruído do objeto,
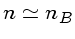 ,
onde, aqui, nB é o número de fótons por segundo do céu,
teremos
,
onde, aqui, nB é o número de fótons por segundo do céu,
teremos
Se desprezarmos as correções
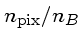 e de digitalização,
podemos escrever a relação sinal-ruído em função do tempo t
como:
e resolver para t:
e de digitalização,
podemos escrever a relação sinal-ruído em função do tempo t
como:
e resolver para t:
Qual das fórmulas usar precisa ser estabelecido, primeiro, comparando o
número de fótons do objeto com o número de fótons do céu, na abertura necessária. Se o objeto for mais fraco que o céu, o problema é muito mais complexo
e não se pode utilizar nenhuma destas duas aproximações.
Podemos determinar o ganho e o ruído de leitura usando dois pares de
imagens: duas imagens de zero (bias) e duas imagens de flat.
Como
para converter o ruido de leitura de contagens (ADU) para elétrons,
precisamos conhecer o ganho real do conversor analógico-digital.
Nas imagens de flat, o ruído poissônico será muito maior do
que o ruído de leitura, e o desvio padrão do flat será:
onde 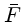 é o valor médio por pixel do flat. Quanto maior o ganho,
maior é o desvio pixel-a-pixel.
Podemos
obter o ganho como:
e
é o valor médio por pixel do flat. Quanto maior o ganho,
maior é o desvio pixel-a-pixel.
Podemos
obter o ganho como:
e
Exemplo de cálculo (HST-WFPC)
Cálculo de exposições SOAR e Gemini.
Dados para imageadores do Soar
Melhor abertura tem raio de 0,725 FWHM
 CCD
CCD
 Fotometria
Fotometria
 Volta: Astronomia e Astrofisica
©
Volta: Astronomia e Astrofisica
©
Modificada em 24 maio 2011
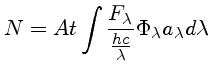
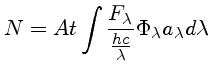
![]() a probabilidade de um evento ocorrer entre
a probabilidade de um evento ocorrer entre
![]() e
e ![]() :
:
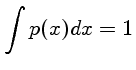
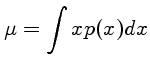
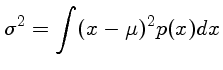
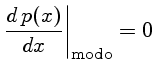
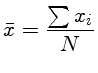
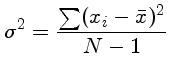
![]() é dada pela
distribuição
de Poisson, descrita por
Siméon-Denis Poisson (1781-1840), como uma
extensão da distribuição binomial - válida quando só há duas soluções
possíveis.
A distribuição de Poisson,
P, é válida quando a probabilidade de
sucesso de cada evento é baixa e o número de tentativas muito grande,
é dada pela
distribuição
de Poisson, descrita por
Siméon-Denis Poisson (1781-1840), como uma
extensão da distribuição binomial - válida quando só há duas soluções
possíveis.
A distribuição de Poisson,
P, é válida quando a probabilidade de
sucesso de cada evento é baixa e o número de tentativas muito grande,
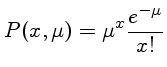
![$\sigma^2 = \sum [(x-\mu)^2 p(x,\mu)] = Np = \mu$](img25.png)
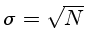 .
.
![]() fotoelétrons (contagens)
detectados de um objeto. O ruído estatístico (Poissoniano) da
medida será dado por
fotoelétrons (contagens)
detectados de um objeto. O ruído estatístico (Poissoniano) da
medida será dado por
![]() .
Mas em um CCD temos outras fontes de ruído:
.
Mas em um CCD temos outras fontes de ruído:
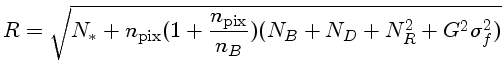


 Flats de céu para o filtro U no Soar Optical Imager.
Flats de céu para o filtro U no Soar Optical Imager.



![]() o número de píxeis da região
(anel) de fundo (background), e
o número de píxeis da região
(anel) de fundo (background), e
![]() o valor médio do fundo por pixel.
O ruído total sobre as
contagens do objeto após a subtração do fundo
será então
o valor médio do fundo por pixel.
O ruído total sobre as
contagens do objeto após a subtração do fundo
será então
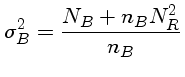
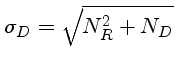
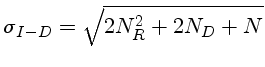
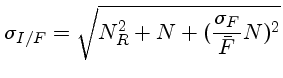
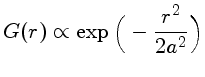
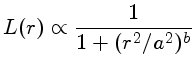
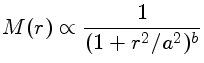
![]() ,
onde, aqui, nB é o número de fótons por segundo do céu,
teremos
,
onde, aqui, nB é o número de fótons por segundo do céu,
teremos
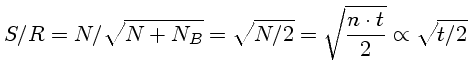
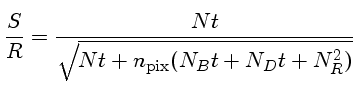
![$t = \frac{{(\frac{S}{R})^2[N+n_{pix}(N_B+N_D)]} +
\sqrt{(\frac{S}{R})^4[N+n_{pix}(N_B+N_D)]^2 +4 N^2 (\frac{S}{R})^2 n_{pix}N_R^2}} {2N^2}$](img4b.png)