Fotometria
Utilizamos a fotometria para medir o fluxo e a cor das estrelas e com esta estimar sua temperatura.
A parte mais importante da fotometria é a escolha do sítio. Somente o céu mais
limpo e consistente pode ser utilizado para fotometria de precisão.
Qualquer quantidade de nuvens, poeira, cintilação, poluição luminosa
e suas variações tornam as medidas incertas. Para medidas no infravermelho,
a quantidade de vapor de água na atmosfera tem que ser mínima.
Por isto os observatórios estão localizados em montanhas
altas, para reduzir o caminho ótico
que a luz tem que atravessar, e desérticas, acima da camada de inversão.
A segunda parte importante é a escolha das estrelas de comparação. Elas
precisam ser não variáveis com alta precisão, estarem próximas
no céu que o objeto a ser medido, ter tipo espectral similar,
ter magnitude aparente similar e ter sua magnitude bem determinada
no sistema fotométrico padrão
a ser utilizado, e não ter nenhuma
estrela próxima para a resolução que se vai observar. Pelo menos
duas estrelas de comparação, de cores diferentes, são necessarias para a determinação
das constantes de transformação do sistema, e precisam
ser observadas a várias massas de ar (distância zenital) para
determinar a absorção atmosférica.
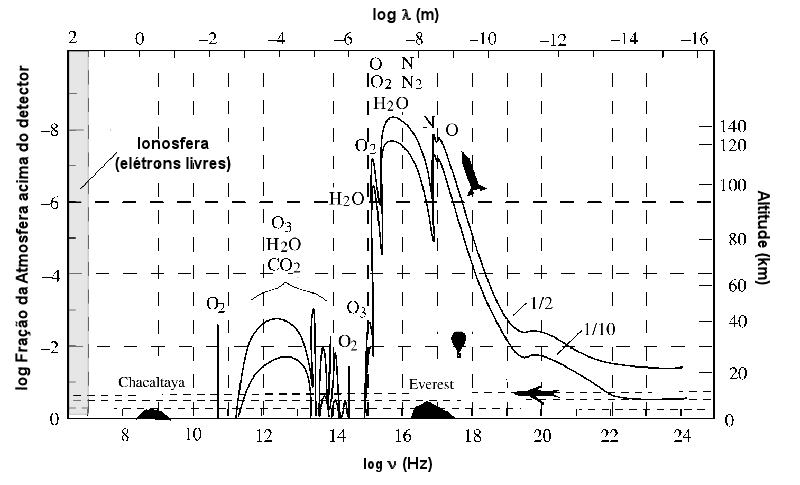 Absorção da luz pela atmosfera da Terra. Na abcissa temos a freqüência
da radiação (em baixo) e o comprimento de onda (em cima). Na ordenada
temos a altura da atmosfera (direita) e a fração da profundidade
da atmosfera em que 1/2 ou 1/10 da radiação incidente sobrevive
até este ponto. Os elementos e moléculas especificados são
a fonte da absorção (Hale Bradt, Astronomy Methods - A Physical
Approach to Astronomical Observations, 2003, Cambridge University Press).
Absorção da luz pela atmosfera da Terra. Na abcissa temos a freqüência
da radiação (em baixo) e o comprimento de onda (em cima). Na ordenada
temos a altura da atmosfera (direita) e a fração da profundidade
da atmosfera em que 1/2 ou 1/10 da radiação incidente sobrevive
até este ponto. Os elementos e moléculas especificados são
a fonte da absorção (Hale Bradt, Astronomy Methods - A Physical
Approach to Astronomical Observations, 2003, Cambridge University Press).
O artigo fundamental de estrelas padrões primárias é
Arlo U. Landolt, 2009,
UBVRI PHOTOMETRIC STANDARD STARS AROUND THE CELESTIAL EQUATOR: UPDATES AND ADDITIONS,
The Astronomical Journal, 137, 4186.
Peter Stetson
mantém sua lista de campos padrões secundários, importantíssimo para quem
estuda aglomerados.
A redução de dados de fotometria é realizada em três estágios - correção dos
efeitos da atmosfera da Terra, transformação ao sistema fotométrico
padrão e correção por avermelhamento interestelar.
Os coeficientes de extinção médios medidos por
estrelas
padrões do Peter Stetson para o FORS2 do VLT do ESO
são:
# file F2_GPHO_111128A_CCID20-14-5-3.fits
# Number of columns 7
#
FILTER| EXT| DEXT| COL| DCOL| ZPOINT| DZPOINT
b_HIGH | 0.2162| 0.0002| 0.10974| 0.004235| 28.0501| 0.01796
v_HIGH | 0.118| 0.0001| 0.057684| 0.0030304| 28.2535| 0.008815
R_SPECIAL| 0.0812| 0.0001|-0.0095598| 0.0072211| 28.2901| 0.02313
I_BESS | 0.0591| 0.0002| -0.017739| 0.011454| 27.6317| 0.02866
# file F2_GPHO_111128A_CCID20-14-5-6.fits
# Number of columns 7
#
FILTER| EXT| DEXT| COL| DCOL| ZPOINT| DZPOINT
b_HIGH | 0.2239| 0.0002| 0.10974| 0.004235| 28.0749| 0.01749
v_HIGH | 0.128| 0.0002| 0.057684| 0.0030304| 28.2439| 0.008391
R_SPECIAL| 0.0848| 0.0002|-0.0095598| 0.0072211| 28.2904| 0.02331
I_BESS | 0.0523| 0.0002| -0.017739| 0.011454| 27.6308| 0.02833
O ESO mantém desde 2012 uma página com
os resultados dos ponto zero e coeficientes de extinção diários.
Eles também têm o resultado
de um workshop discutindo a precisão da fotometria absoluta que se pode obter com o instrumento.
O artigo Empirical extinction coefficients for the GALEX, SDSS, 2MASS and WISE passbands, de
Hai-Bo Yuan, Xiao-Wei Liu, Mao-Sheng Xiang,
publicado no Monthly Notices of the Royal Astronomical Society, 430, 2188-2199 (2013), traz os coeficientes
da razão entre a extinção total e a seletiva, R(λ) atuais:
R(FUV)=4.89±0.60
R(NUV)=4.24±0.08
R(u)=4.39±0.04
R(g)=3.30±0.03
R(r)=2.31±0.03
R(i)=1.71±0.02
R(z)=1.29±0.02
R(J)=0.72±0.01
R(H)=0.46±0.01
R(KS)=0.31±0.01
R(W1)=0.18±0.01
R(W2)=0.16±0.01
Para analisar a variabilidade de um objeto, também será necessário transformar
o tempo de observação ao baricentro do sistema solar, corrigindo pelo
movimento da Terra em torno deste.
A base de tempo utilizada nos relógios é o UTC (Tempo Universal
Coordenado), com a introdução de segundos bissextos (leap seconds)
para permitir a pequena taxa de mudança no período de rotação real
da Terra mas mantendo a definição de 1 segundo do tempo atômico
como a unidade de tempo
(1 s= 9 192 631 770 ciclos do Cs133).
A rotação da Terra varia cerca de 1,7 ms/século em relação
ao segundo atômico, que define o Tempo Atômico Internacional (TAI).
Como os astrônomos necessitam de um padrão de tempo contínuo, que não
seja ajustado pelas irregularidades da rotação da Terra, usam o
Tempo Terrestre, adicionando 32,184 s ao TAI.
TT=UTC+32,184+leap
De 1 de janeiro de 2009 até 30 junho de 2012, leap=34 s.
De 1 de julho de 2012 até 30 junho de 2015, leap=35 s.
De 1 de julho de 2015 até 31 dezembro de 2016, leap=36 s.
Desde 1 de janeiro de 2017, leap=37 s.
A tabela de leap
seconds é mantida pelo
International
Earth Rotation and Reference Systems Service.
Em 1991 a União Astronômica Internacional definiu o
Tempo Coordenado Baricêntrico (TCB), com origem no baricentro
do sistema solar. Ele precisa ser calculado levando-se em
conta a órbita de todos os corpos do sistema solar,
a dilatação do tempo devido à velocidade da Terra
em relação ao baricentro (0,0001 c) e a correção pela relatividade
geral do potencial gravitacional do sistema (49 s/século).
A correção vai a 499,00 s (1 U.A./c=8,3 m) ao centro do Sol
e 2,5 s deste ao baricentro, já que
rSol-centro de massa=rJúpiter-centro de massa × MJúpiter/MSol=
5,2 UA × MJúpiter/MSol
= 745 mil km = 2,47 s c
A Resolução 3 da IAU 2006 estabelece que
Tempo Coordenado Baricêntrico é a coordenada de tempo para uso no Sistema de Referência Baricêntrico Celestial.
Portanto o tempo no baricentro do sistema solar é aproximadamente dado por
tbaricentro=tTerra+501,47 s
[senδ*senδbaricentro
-cos(δ*cosδbaricentro
cos(αbaricentro-α*)]
onde tTerra é o tempo da observação em dias geocêntricos,
tbaricentro o tempo correspondente no baricentro
do sistema solar, α* e δ*
as coordenadas da estrela,
e αbaricentro e δbaricentro
as coordenadas do baricentro solar, que precisam
ser calculadas com um modelo do sistema solar,
mantidos pelo International Earth Rotation and
Reference Systems Service.
Uma correção mais precisa leva em conta a variação da distância,
assumida aqui como 501,5 s-luz.
Um cálculo pode ser feito em UTC2BJD.
Próxima:Tratamento de Dados dos CCDs
Volta: Telescópios
Anterior: Detectores
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 9 abril 2018
