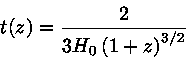Efeitos da Constante Cosmológica
Se a constante cosmológica não for nula, o Universo se torna
dominado por uma densidade de energia do vácuo
positiva, constante e não nula
 . A evolução da métrica
neste caso logo se aproxima de
. A evolução da métrica
neste caso logo se aproxima de
Enquanto a luz viaja da fonte ao observador, seu comprimento
de onda se expande por um fator proporcional ao aumento de a(t).
Se atualmente Λ
contribui com 71% da densidade de energia
total em um universo plano (K=0, Ωtotal=1), então o Universo se tornou
dominado por
Λ, isto é, pela energia escura, em cerca de metade da idade atual.
Podemos expressar a idade em função do deslocamento para
o vermelho 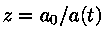 , da razão da densidade de matéria
para a densidade crítica,
, da razão da densidade de matéria
para a densidade crítica, 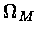 , e da razão da
densidade de energia do vácuo para a densidade crítica,
, e da razão da
densidade de energia do vácuo para a densidade crítica,
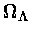 , como
, como
Se o Universo é plano, e sabendo que Ωr=8,35×10-5 é desprezível atualmente,
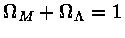 e a integral resulta em
e a integral resulta em
No limite
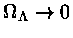 , recuperamos a
relação entre a idade e o deslocamento para o vermelho
de um universo plano sem energia escura:
, recuperamos a
relação entre a idade e o deslocamento para o vermelho
de um universo plano sem energia escura:
PróximaRecombinação
Volta: Cosmologia Matemática
 Astronomia e Astrofisica
Astronomia e Astrofisica
©
Modificada em 5 jan 2018
![a(t) = a_0 \exp [\sqrt{\frac{\Lambda}{3}}(t-t_0)]](img2.gif)
![a(t) = a_0 \exp [\sqrt{\frac{\Lambda}{3}}(t-t_0)]](img2.gif)
![]() , da razão da densidade de matéria
para a densidade crítica,
, da razão da densidade de matéria
para a densidade crítica, ![]() , e da razão da
densidade de energia do vácuo para a densidade crítica,
, e da razão da
densidade de energia do vácuo para a densidade crítica,
![]() , como
, como
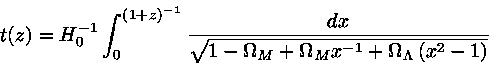
![t(z) = \frac{2}{3H_0\sqrt{\Omega_\Lambda}}
\ln [\sqrt{\f...
...Omega_\Lambda}{1-\Omega_\Lambda}(1+z\right)^{-3}+1}]](img9.gif)