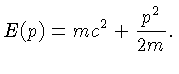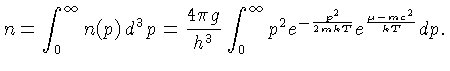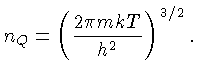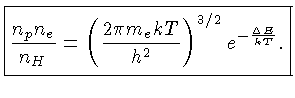

Volta: Cosmologia Matemática
Anterior: Cosmologia na Relatividade Geral
Intuitivamente espera-se que quando a energia média de um fóton
da radiação do fundo do Universo caisse abaixo de 13,6 eV,
a energia de ionização do hidrogênio, a maior parte do
hidrogênio torna-se-se neutra. Podemos definir
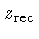 como o desvio para o vermelho (redshift) para o qual
os elétrons e prótons recombinam, formando o hidrogênio
neutro. O termo recombinação, usado por James Peebles em 1950,
é um pouco problemático, pois nesta época da evolução
do Universo, os elétrons e prótons estavam se combinando pela
primeira vez.
como o desvio para o vermelho (redshift) para o qual
os elétrons e prótons recombinam, formando o hidrogênio
neutro. O termo recombinação, usado por James Peebles em 1950,
é um pouco problemático, pois nesta época da evolução
do Universo, os elétrons e prótons estavam se combinando pela
primeira vez.
Na verdade, como veremos a seguir, a temperatura de recombinação
é da ordem de 5 vezes menor do que a correspondente a 13,6 eV,
porque o espaço de fase dos elétrons livres é muito maior
do que o espaço de fase dos elétrons ligados, o que
faz com que os elétrons permaneçam livres por mais tempo.
Consideremos a reação
Em equilíbrio químico, temos:
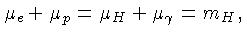 |
(1.30) |
já que o potencial químico dos fótons é nulo. Nesta
equação, 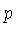 representa o próton.
representa o próton.
A equação de Saha é obtida combinando-se esta expressão
com a função distribuição para as espécies em
questão:
onde 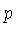 é o momentum,
é o momentum, 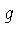 é o fator de degenerescência, o
sinal mais se aplica aos férmions, isto é, partículas
que obedecem à distribuição de momentum de Fermi-Dirac,
como os prótons e os elétrons,
e o sinal menos é para os bósons, isto é, partículas
que obedecem à distribuição de Bose-Einstein, como os fótons.
A função distribuição é definida de forma que
é o fator de degenerescência, o
sinal mais se aplica aos férmions, isto é, partículas
que obedecem à distribuição de momentum de Fermi-Dirac,
como os prótons e os elétrons,
e o sinal menos é para os bósons, isto é, partículas
que obedecem à distribuição de Bose-Einstein, como os fótons.
A função distribuição é definida de forma que
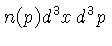 é o número de partículas
no elemento de volume
é o número de partículas
no elemento de volume
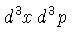 do espaço de fase.
Como estamos interessados em energias próximas a 13,6 eV,
os elétrons e os prótons são não relativísticos,
do espaço de fase.
Como estamos interessados em energias próximas a 13,6 eV,
os elétrons e os prótons são não relativísticos,
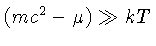 ,
Assumindo que as densidades eram não
degeneradas, a densidade de partículas pode
ser escrita como a distribuição de Boltzmann:
Integrando, obtemos:
,
Assumindo que as densidades eram não
degeneradas, a densidade de partículas pode
ser escrita como a distribuição de Boltzmann:
Integrando, obtemos:
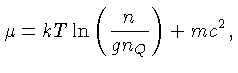 |
(1.31) |
onde a densidade quântica 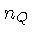 é definida como:
Colocando-se o valor do potencial químico (31)
na equação do equilíbrio químico (30), obtemos:
é definida como:
Colocando-se o valor do potencial químico (31)
na equação do equilíbrio químico (30), obtemos:
![$kT[\ln(\frac{n_e}{g_en_{Qe}}) +\ln(\frac{n_p...) -\ln(\frac{n_H}{g_Hn_{QH}})]= (m_H-m_p-m_e)c^2.$](img319.gif) |
(1.32) |
Nesta equação voltamos a usar 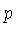 para representar um próton,
e não o momentum. O termo da direita da equação (32)
é a energia de ligação do hidrogênio,
para representar um próton,
e não o momentum. O termo da direita da equação (32)
é a energia de ligação do hidrogênio,
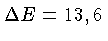 eV.
Os fatores de degenerescência são
eV.
Os fatores de degenerescência são 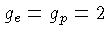 e
e 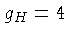 .
Assumindo
.
Assumindo
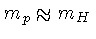 nos valores de
nos valores de 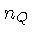 ,
obtemos a equação de Saha para a reação:
Definindo a fração de ionização
,
obtemos a equação de Saha para a reação:
Definindo a fração de ionização 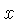 por
por
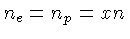 , onde a densidade total
, onde a densidade total
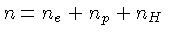 ,
obtemos uma equação transcendental para
,
obtemos uma equação transcendental para 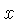 em
termos do desvio para o vermelho
em
termos do desvio para o vermelho  substituindo-se
substituindo-se
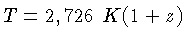 e
e
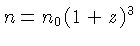 . O desvio para o vermelho
para a época de recombinação
. O desvio para o vermelho
para a época de recombinação 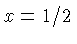 pode ser
obtido usando o valor da densidade de partículas no
presente,
já que o hidrogênio compõe aproximadamente 75%
da massa bariônica do Universo, obtemos
A temperatura nesta época era de
muito menor do que 13,6 eV.
Podemos utilizar uma massa média de bárions um pouco mais precisa,
pois quase a totalidade dos 25% restantes de massa em bárions está
na forma de átomos de hélio, de modo que:
Logo após a recombinação temos a época do desacoplamento
da radiação com a matéria, uma vez que quando os elétrons
e prótons combinam-se, o Universo se torna muito menos opaco.
Os elétrons ligados só são capazes de interagir com
os fótons com energia discretas, correspondentes aos
níveis de excitação, ou com energias maiores do
que a energia de ionização, mas como vimos a energia
média dos elétrons é muito menor do que esta energia.
O livre caminho médio dos fótons torna-se então muito
grande, já que eles viajam grandes distâncias
sem interagir com a matéria. Dizemos então que a
radiação está desacoplada da matéria.
pode ser
obtido usando o valor da densidade de partículas no
presente,
já que o hidrogênio compõe aproximadamente 75%
da massa bariônica do Universo, obtemos
A temperatura nesta época era de
muito menor do que 13,6 eV.
Podemos utilizar uma massa média de bárions um pouco mais precisa,
pois quase a totalidade dos 25% restantes de massa em bárions está
na forma de átomos de hélio, de modo que:
Logo após a recombinação temos a época do desacoplamento
da radiação com a matéria, uma vez que quando os elétrons
e prótons combinam-se, o Universo se torna muito menos opaco.
Os elétrons ligados só são capazes de interagir com
os fótons com energia discretas, correspondentes aos
níveis de excitação, ou com energias maiores do
que a energia de ionização, mas como vimos a energia
média dos elétrons é muito menor do que esta energia.
O livre caminho médio dos fótons torna-se então muito
grande, já que eles viajam grandes distâncias
sem interagir com a matéria. Dizemos então que a
radiação está desacoplada da matéria.


Volta: Cosmologia Matemática
Anterior: Cosmologia na Relatividade Geral
©
Modificada em 6 fev 1999
![$n(p) = \frac{g}{h^3}[\exp(\frac{E(p)-\mu}{kT})\pm 1]^{-1}$](img309.gif)