
Em um sistema de coordenadas Euclidiano, a unidade de distância não
varia com a posição.
Carl Friedrich Gauss (1777-1855)
propôs um sistema de coordenadas geral, não Euclidiano;
imaginemos um sistema de coordenadas de curvas arbitrárias,
não justapostas, em uma superfície qualquer.
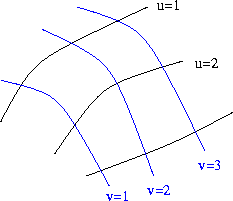
Em uma direção designemos as curvas por ![]() , designando-as
, designando-as
![]() ,
, ![]() , .... Entre as curvas
, .... Entre as curvas ![]() e
e ![]() podemos imaginar
um número infinito de curvas, correspondendo aos números naturais
entre 1 e 2. As curvas não se intersectam e
somente uma curva passa por cada ponto da superfície,
de modo que um valor perfeitamente definido de
podemos imaginar
um número infinito de curvas, correspondendo aos números naturais
entre 1 e 2. As curvas não se intersectam e
somente uma curva passa por cada ponto da superfície,
de modo que um valor perfeitamente definido de ![]() pode ser estabelecido
para cada ponto. Podemos estabelecer um sistema
pode ser estabelecido
para cada ponto. Podemos estabelecer um sistema ![]() de
coordenadas sobre a superfície, de modo que um valor
de
de
coordenadas sobre a superfície, de modo que um valor
de ![]() e
e ![]() possam ser estabelecidos para cada ponto da superfície.
Chamamos estes pontos de coordenadas gaussianas da superfície.
Dois pontos próximos terão coordenadas
possam ser estabelecidos para cada ponto da superfície.
Chamamos estes pontos de coordenadas gaussianas da superfície.
Dois pontos próximos terão coordenadas ![]() e
e ![]() ,
com coordenadas:
,
com coordenadas:
Podemos generalizar as coordenadas de Gauss para um contínuo de três ou mais dimensões. Para um contínuo de quatro dimensões, como o espaço de Minkowski, podemos escrever que dois pontos adjacentes estão separados por uma distância:
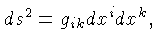
Por exemplo, para um sistema de coordenadas esféricas no espaço plano: