

Próxima: Levantando e Baixando Índices
Volta: Cosmologia Relativística
Anterior: Coordenadas Gaussianas
Relatividade Geral
Na relatividade geral, a velocidade da luz não é mais mantida
constante, mas depende do sistema de coordenadas quando um
campo gravitacional está presente. A idéia fundamental
da relatividade geral é que todos sistemas de coordenadas gaussianos
são equivalentes para a formulação das leis gerais da natureza,
de modo que as equações não devem mudar de forma ao
serem submetidas a substituições arbitrárias das
variáveis gaussianas. As transformações
de Lorentz não satisfazem esta condição.
A equação de campo de Einstein
[Albert Einstein,
Sitzungsberichte der Preuβische Akademie der Wissenschaften
(Berlin), 844 (1915)]
modificada para incluir a constante cosmológica Λ
[Albert Einstein, Sitzungsberichte der Preuβische Akademie der Wissenschaften
(Berlin), 142 (1917)]
pode ser escrita como:
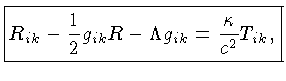 |
(1.22) |
onde 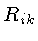 é o
tensor espaço-tempo,
é o
tensor espaço-tempo,
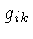 são as componentes do
tensor métrico e dependem do
sistema de coordenadas usado e da unidade da coordenada temporal,
são as componentes do
tensor métrico e dependem do
sistema de coordenadas usado e da unidade da coordenada temporal,
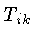 é o tensor momentum-energia,
que depende da distribuição e movimento das
massas e do campo eletromagnético,
é o tensor momentum-energia,
que depende da distribuição e movimento das
massas e do campo eletromagnético,
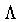 é a constante cosmológica, que pode
ser nula, e
é a constante gravitacional de Einstein.
Na equação (22), onde os dois índices
i
e
k
variam de 0 a 3 e
R=gikRik é o traço, necessário
para que o divergente covariante do lado esquerdo seja nulo,
já que a divergência covariante do tensor energia-momentum
é nula
pela conservação de energia-momentum no limite
da relatividade especial.
Os
dois primeiros termos à esquerda do sinal de igualdade representam
a curvatura do espaço-tempo,
o termo à direita as forças que atuam neste sistema
e o terceiro termo à esquerda, da constante cosmológica
é a constante cosmológica, que pode
ser nula, e
é a constante gravitacional de Einstein.
Na equação (22), onde os dois índices
i
e
k
variam de 0 a 3 e
R=gikRik é o traço, necessário
para que o divergente covariante do lado esquerdo seja nulo,
já que a divergência covariante do tensor energia-momentum
é nula
pela conservação de energia-momentum no limite
da relatividade especial.
Os
dois primeiros termos à esquerda do sinal de igualdade representam
a curvatura do espaço-tempo,
o termo à direita as forças que atuam neste sistema
e o terceiro termo à esquerda, da constante cosmológica 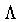 ,
representa a energia do vácuo, que normalmente é assumida nula.
Para pequenas regiões do espaço-tempo, o espaço pode
ser considerado plano e as coordenadas Lorentzianas. Neste caso,
,
representa a energia do vácuo, que normalmente é assumida nula.
Para pequenas regiões do espaço-tempo, o espaço pode
ser considerado plano e as coordenadas Lorentzianas. Neste caso,
Para um gás, o tensor energia-momentum em coordenadas curvilíneas
pode ser escrito como:
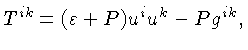 |
(1.23) |
onde
é a densidade de energia da matéria, incluindo a energia de repouso,
medida no sistema em repouso com a matéria,
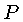 é a pressão isotrópica,
e
é a quadri-velocidade do gás.
é a pressão isotrópica,
e
é a quadri-velocidade do gás.
A conservação de energia-momentum é expressa pela
lei fundamental de geometria:
A equação (22) pode ser escrita como:
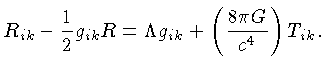 |
(1.24) |
A equação da geodésica (world line) de
uma partícula pode ser definida
em termos do seu tempo próprio 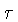 e da sua quadri-velocidade
e da sua quadri-velocidade 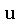 como:
como:
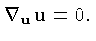 |
(1.25) |
Escolhendo-se um sistema de coordenadas tal que:
podemos escrever os componentes da equação (25) como:
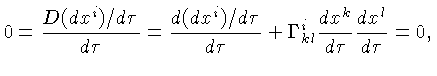 |
(1.26) |
onde
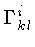 são os símbolos de Christoffel
[Elwin Bruno Christoffel (1829-1900)],
se as coordenadas formam uma base:
Note que,
na equação (26),
as componentes da ``derivada'' (
são os símbolos de Christoffel
[Elwin Bruno Christoffel (1829-1900)],
se as coordenadas formam uma base:
Note que,
na equação (26),
as componentes da ``derivada'' (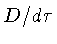 ) precisam ser corrigidas pelos
termos proporcionais aos símbolos de Christoffel porque
as coordenadas generalizadas de Gauss podem variar rapidamente,
levando a mudanças nas componentes de um vetor
mesmo que o vetor não varie.
) precisam ser corrigidas pelos
termos proporcionais aos símbolos de Christoffel porque
as coordenadas generalizadas de Gauss podem variar rapidamente,
levando a mudanças nas componentes de um vetor
mesmo que o vetor não varie.
Ou seja, a equação em coordenadas curvilíneas que define a linha
geodésica (linha que seguirá uma partícula livre)
conectando dois pontos no espaço-tempo
é dada por:
que pode ser resolvida especificando-se os valores iniciais de
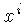 e
e
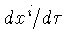 para
para
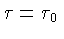 .
.
Para descrever completamente um espaço-tempo curvo,
o matemático alemão
Georg Friedrich Bernhard Riemann (1826-1866),
que obteve seu doutorado sob a supervisão de Gauss, demonstrou que é
preciso de um tensor de ordem 4:
chamado de tensor de curvatura de Riemann. Com este tensor de quarta
ordem podemos construir um tensor de segunda ordem por contração:
onde índices repetidos significam soma,
pela convenção da soma de Einstein. Este tensor de segunda
ordem é chamado de tensor Ricci [Georgorio Ricci-Curbastro (1853-1925)],
que contraído nos
dá a curvatura escalar do espaço-tempo:
A densidade de massa-energia, medida por um observador de
quadri-velocidade 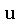 é dada por:
é dada por:


Próxima: Levantando e Baixando Índices
Volta: Cosmologia Relativística
Anterior: Coordenadas Gaussianas
©
Modificada em 10 dez 2012
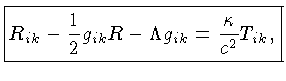
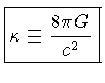
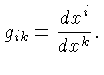
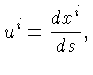
![]() e da sua quadri-velocidade
e da sua quadri-velocidade ![]() como:
como:
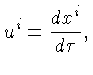
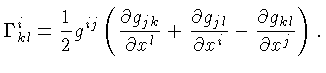
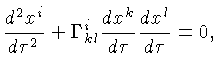
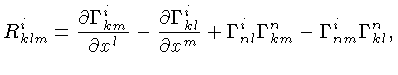
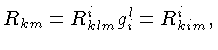
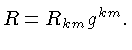
![]() é dada por:
é dada por: