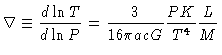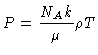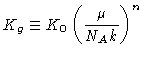No envelope, podemos assumir
Lr = L e
Mr=M, isto é,
a contribuição do envelope para a luminosidade e para a massa
é desprezível. Se o envelope for radiativo,
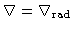 ou seja
ou seja
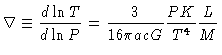 |
(40) |
Vamos assumir no momento que a pressão de radiação seja
desprezível, e que a opacidade pode ser escrita de
forma geral como
K=K0 ⍴n T-s. Para um gás ideal
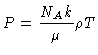 |
(41) |
e, substituindo a densidade ⍴ em termos de P/T,
podemos expressar o coeficiente de absorção
onde
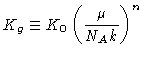 |
(43) |
Com esta substituição, a equação do gradiente radiativo (40) contém somente P e T
como variáveis, já que estamos assumindo
M e
L
constantes no envelope. Podemos reescreve-la como
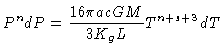 |
(44) |
Se 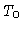 e
e 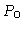 representam a temperatura e a pressão em algum
ponto exterior do envelope, como a fotosfera, de modo que
representam a temperatura e a pressão em algum
ponto exterior do envelope, como a fotosfera, de modo que
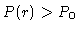 e
e 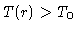 , podemos integrar a equação (44)
e obter
, podemos integrar a equação (44)
e obter
![$P^{n+1} = \frac{n+1}{n+s+4}\frac{16\pi acGM}{3K_gL}T^{n+s+4} [\frac{1-(T_0/T)^{n+s+4}}{1-(P_0/P)^{n+1}}]$](img88.gif) |
(45) |
Desta forma, assumindo P0=Pf dado pela equacão
(39)
obtemos a pressão no envelope para uma temperatura T qualquer.



Próxima: Estrelas Completamente Convectivas
Volta: Condições de Contorno
Anterior: Atmosferas Estelares
 Evolução Estelar
Evolução Estelar
©