Transições Ligado-Livre

Como um exemplo, $a_0^H(912\AA,1)=6,3\times 10^{-18}~{{cm^2}}$, já que a freqüência correspondente a $\lambda=912$ Å é  $\nu=3,29 \times 10^{-15}$ Hz.

Para uma composição química similar à do Sol, a média de Rosseland,

K_bf,R≃40 000 cm²/g Z(1+X) (ρ/1 g cm^-3) [T/(10⁶ K)]^-3,5

Transições Livre-Livre

Como um exemplo, para o núcleo do Sol, com $T=10^7$ K, $\rho\simeq 100~{{g/cm^3}}$, ou seja, $n_e \simeq n_H \simeq 6 \times 10^{25}~{{cm^{-3}}}$, para $\lambda=912$ Å, $F\simeq 1$ e $a_{ff} \simeq 2\times 10^{-16}~{{cm^2}}$.

K_ff,R≃40 cm²/g (1+X)(1-Z) (ρ/1 g cm^-3) [T/(10⁶ K)]^-3,5

ou seja, K_ff,R/K_bf,R≃1000 Z/(1-Z).

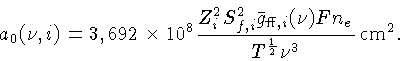
Quando a média de Rosseland é calculada, tanto a K_bf,R quanto a K_ff,R seguem uma lei de Kramers, K_R∝ρT^-3,5.

Espalhamento por elétrons

$$\sigma_0 \frac{8\pi}{3}(\frac{e^2}{m_ec^2})^2$$ ~0,6652×10^-24cm²=0,6625 barn

enquanto os prótons têm uma seção de choque da ordem de 100 kilibarns.

Assumindo neutralidade de carga, o livre caminho médio dos elétrons

λ_e=1/(n_eσ_e)=1/2 m_p/(ρσ_e)≃3,7×10^-6 cm (ρ_⊙/ρ) (v^térmica_e/0,05c)⁴

enquanto o livre caminho médio do fóton, assumindo que o espalhamento dos elétrons seja dominante, é λ_fóton=1/(n_eK)=1,8 cm (ρ_⊙/ρ)

Devido à dependência com T^-3,5 da opacidade de Kramers, o espalhamento de elétrons domina sobre a absorção em altas temperaturas, mas somente para T>4×10⁷ K para a densidade central do Sol, de ρ=153 g/cm³, cerca de 3× a temperatura central do Sol.

Próxima: Geração de Energia Nuclear Volta: Evolução Estelar
Volta: Astronomia e Astrofisica