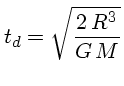Tempo termico

Tempo térmico

Outra fonte de energia que o Sol e as outras estrelas têm, e que é importante quando estão se contraindo e ainda não produzem energia nuclear, é a energia resultante da contração gravitacional. Por conservação de energia, quando a energia gravitacional diminui (devido à contração), aumenta a energia cinética das partículas dentro da estrela, ou seja, aumenta a energia térmica. Nessa fase a energia total da estrela é:

onde é energia gravitacional e é energia térmica.

Pelo teorema do Virial, que se aplica a gases perfeitos, a energia total é igual à metade da energia potencial gravitacional:

$E_G + E_T = \frac{1}{2} E_G$

Portanto, quando a estrela se contrai, apenas metade da energia é usada para aumentar sua temperatura, a outra metade é liberada na forma de radiação (luminosidade). Considerando que a energia potencial gravitacional de uma esfera auto-gravitante de massa e raio é da ordem de , a energia gerada pela contração que é disponível para ser irradiada é:

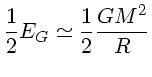
$\frac{1}{2} E_G = \frac{1}{2}\frac{GM^2}{R}$

O tempo durante o qual a contração gravitacional poderia sustentar a luminosidade do Sol no seu valor atual é chamado tempo térmico, ou tempo de contração de Kelvin ( $t_{K}$ ):

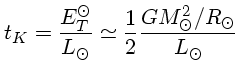
$t_{K} = \frac{E_T^{\odot}}{L_\odot} =\frac{1}{2}\frac{GM_\odot^2/R_\odot}{L_\odot}$

Substituindo os valores de G = 6,67 × 10^-11 N m²/kg², M_Sol = 1,99 × 10³⁰ kg; R_Sol = 6,95 × 10⁸ m, e L_Sol = 3,9 × 10²⁶ J/s, temos:

t_K=20×10⁶ anos

Tempo dinâmico

É o tempo que dura o colapso da estrela se as forças de pressão que suportam o peso das camadas superiores fossem removidas. É o tempo de queda-livre que, para uma estrela de massa M e raio R e vale

$t_d = \sqrt{\frac{2 R^3}{G M}}$

Para o Sol, esse tempo dura em torno de 1/4 hora.

Próxima: Energia Nuclear de Ligação Volta: Escalas de tempo evolutivo Anterior: Tempo nuclear