Consideremos uma estrela fria cuja opacidade superficial seja
dominada por
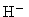 ; o coeficiente de absorção pode ser
estimado por
; o coeficiente de absorção pode ser
estimado por
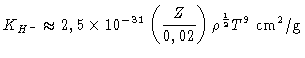 |
(46) |
A relação entre temperatura e pressão dada pela eq. (45)
pode ser transformada em uma equação para
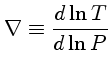 em função
da temperatura
em função
da temperatura
![$\nabla = \frac{1}{1+n_{ef}}+(\frac{T_{ef}}{T})^{n+s+4} [\nabla_f - \frac{1}{1+n_{ef}}]$](img92.gif) |
(47) |
onde
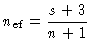 |
(48) |
e o subscrito 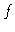 significa fotosférico, isto é,
significa fotosférico, isto é, 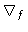 é
é  calculado na fotosfera. De acordo com eq. (40):
calculado na fotosfera. De acordo com eq. (40):
Na fotosfera,
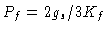 ,
,
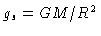 e
e
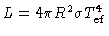 , de modo que
, de modo que
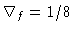 .
Abaixo da fotosfera, a eq. (47), com
.
Abaixo da fotosfera, a eq. (47), com
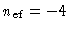 para a opacidade do
para a opacidade do
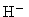 se reduz a
se reduz a
![$\nabla(r) = - \frac{1}{3}+\frac{11}{24} [\frac{T_{ef}}{T(r)}]^{-\frac{9}{2}}$](img104.gif) |
(51) |
Como a temperatura cresce com a profundidade, 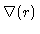 também cresce.
Em algum ponto
também cresce.
Em algum ponto 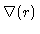 tornar-se-a maior do que
tornar-se-a maior do que
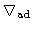 e a camada interior será convectiva. Por exemplo, se assumirmos
que
e a camada interior será convectiva. Por exemplo, se assumirmos
que
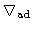 é dado pelo seu valor de gás ideal,
sem ionização,
é dado pelo seu valor de gás ideal,
sem ionização,
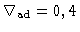 , podemos estimar
a temperatura para a qual
, podemos estimar
a temperatura para a qual
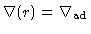 . Para
a região interior teremos um polítropo de índice 3/2
e
. Para
a região interior teremos um polítropo de índice 3/2
e
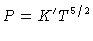 |
(52) |
como demonstramos na seção de polítropos. Desta maneira,
teremos uma fotosfera, de onde escapa a radiação, sobre
uma camada radiativa, e sob esta, uma zona de convecção,
como no caso do Sol.
No caso extremo em que a convecção continua até o centro da
estrela, a constante 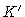 precisa satisfazer as condições de contorno centrais, e
portanto a constante
precisa satisfazer as condições de contorno centrais, e
portanto a constante 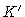 precisa ser a
do polítropo.
Vamos escrever a temperatura e a pressão em termos de variáveis
adimensionais
precisa ser a
do polítropo.
Vamos escrever a temperatura e a pressão em termos de variáveis
adimensionais
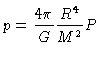 |
(53) |
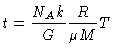 |
(54) |
de modo que a equação (52) se torna
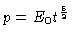 |
(55) |
com
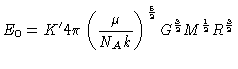 |
(56) |
Como para um
polítropo representando um
gás ideal o índice é n=3/2 e 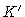 é dado pela
equação 14 dos polítropos
é dado pela
equação 14 dos polítropos
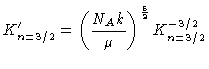 |
(57) |
e substituindo a constante 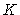 do polítropo
(equação 31 dos polítropos)
do polítropo
(equação 31 dos polítropos)
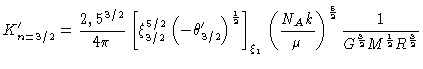 |
(58) |
e concluímos que 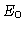 não depende de nenhum parâmetro físico
do modelo, mas somente dos valores superficiais das variáveis
politrópicas, sendo uma constante:
não depende de nenhum parâmetro físico
do modelo, mas somente dos valores superficiais das variáveis
politrópicas, sendo uma constante:
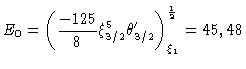 |
(59) |
utilizando os valores da tabela dos polítropos.
Podemos agora calcular o valor da temperatura e densidade no
ponto interior à fotosfera onde
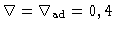 .
Utilizando os valores
.
Utilizando os valores
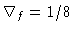 , e os expoentes
, e os expoentes 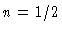 e
e 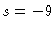 da opacidade de
da opacidade de
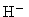 na equação
(47), obtemos
na equação
(47), obtemos
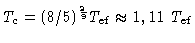 |
(60) |
isto é, a temperatura no topo da zona de conveção
é somente 11% maior do que a temperatura efetiva, comprovando que
a convecção inicia logo abaixo da fotosfera.
A pressão 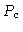 no topo da camada convectiva é obtida
reescrevendo a equação (45) na forma
no topo da camada convectiva é obtida
reescrevendo a equação (45) na forma
![$(\frac{P}{P_f})^{n+1} = 1+ \frac{1}{1+n_{ef}} \frac{1}{\nabla_f}[(\frac{T}{T_{ef}})^{n+s+4}-1]$](img125.gif) |
(61) |
que resulta em
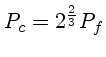 .
Podemos agora substituir
.
Podemos agora substituir
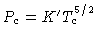 na equação (58) obtendo
na equação (58) obtendo
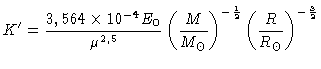 |
(62) |
Como a pressão fotosférica é dada por 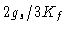 ,
,
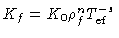 e
a densidade pode ser eliminada usando-se a equação de
estado de um gás ideal,
e
a densidade pode ser eliminada usando-se a equação de
estado de um gás ideal,
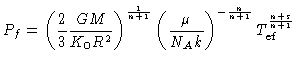 |
(63) |
Podemos utilizar
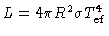 para eliminar as dependências em
para eliminar as dependências em 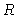 ,
e escrever, para n=1/2 e
,
e escrever, para n=1/2 e 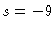 da opacidade
da opacidade
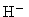
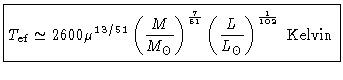 |
(64) |
A constante obtida, de 2600 K, na realidade é próxima de 4000 K,
mas esta relação representa uma série de linhas
quase verticais no diagrama H-R, uma para cada valor de 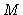 e com
e com
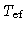 praticamente independente de
praticamente independente de 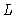 para cada valor de
para cada valor de 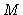 .
.
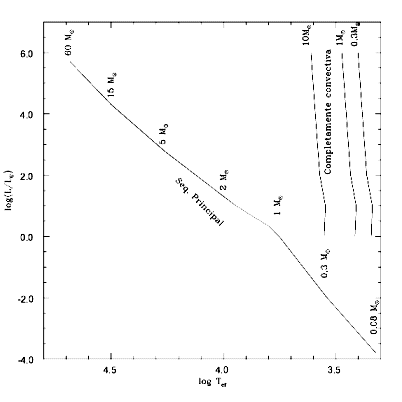
Variação da luminosidade com a temperatura para uma estrela
completamente convectiva de massa
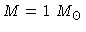
. Para
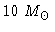
,
a temperatura será somente 37% maior.
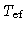 |
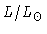 |
| 2600 |
1 |
| 2569 |
10 |
| 2720 |
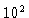 |
| 2782 |
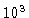 |
| 2846 |
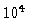 |
| 2911 |
 |
| 2977 |
 |
Note que embora a zona convectiva superficial do modelo
com uma massa solar abranja somente 0,35% da massa isto
corresponde a 17% do raio.



Próxima: Resultado dos Modelos
Volta: Condições de Contorno
Anterior: Envelope Radiativo
Volta: Interiores Estelares
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 7 maio 2006
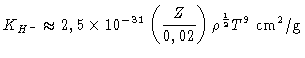
![$P^{n+1} = \frac{n+1}{n+s+4}\frac{16\pi acGM}{3K_gL}T^{n+s+4} [\frac{1-(T_0/T)^{n+s+4}}{1-(P_0/P)^{n+1}}]$](img88.gif)
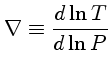 em função
da temperatura
em função
da temperatura
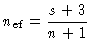
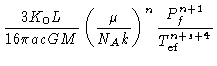
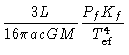
![$\nabla(r) = - \frac{1}{3}+\frac{11}{24} [\frac{T_{ef}}{T(r)}]^{-\frac{9}{2}}$](img104.gif)
![]() também cresce.
Em algum ponto
também cresce.
Em algum ponto ![]() tornar-se-a maior do que
tornar-se-a maior do que
![]() e a camada interior será convectiva. Por exemplo, se assumirmos
que
e a camada interior será convectiva. Por exemplo, se assumirmos
que
![]() é dado pelo seu valor de gás ideal,
sem ionização,
é dado pelo seu valor de gás ideal,
sem ionização,
![]() , podemos estimar
a temperatura para a qual
, podemos estimar
a temperatura para a qual
![]() . Para
a região interior teremos um polítropo de índice 3/2
e
. Para
a região interior teremos um polítropo de índice 3/2
e
![]() precisa satisfazer as condições de contorno centrais, e
portanto a constante
precisa satisfazer as condições de contorno centrais, e
portanto a constante ![]() precisa ser a
do polítropo.
Vamos escrever a temperatura e a pressão em termos de variáveis
adimensionais
precisa ser a
do polítropo.
Vamos escrever a temperatura e a pressão em termos de variáveis
adimensionais
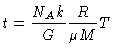
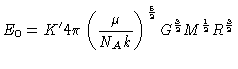
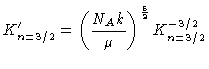
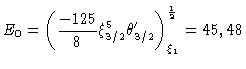
![]() .
Utilizando os valores
.
Utilizando os valores
![]() , e os expoentes
, e os expoentes ![]() e
e ![]() da opacidade de
da opacidade de
![]() na equação
(47), obtemos
na equação
(47), obtemos
![]() no topo da camada convectiva é obtida
reescrevendo a equação (45) na forma
no topo da camada convectiva é obtida
reescrevendo a equação (45) na forma
![$(\frac{P}{P_f})^{n+1} = 1+ \frac{1}{1+n_{ef}} \frac{1}{\nabla_f}[(\frac{T}{T_{ef}})^{n+s+4}-1]$](img125.gif)
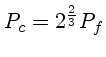 .
Podemos agora substituir
.
Podemos agora substituir
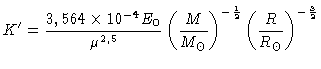
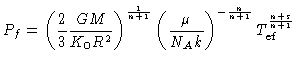
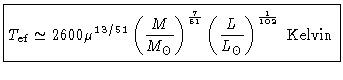
![]()