Uma derivada contravariante é definida como
enquanto que uma derivada covariante é definida como
Portanto um tensor contravariante é dado por
enquanto que um tensor covariante é dado por
Na convenção usual, associamos as componentes contravariantes
de um tensor com um vetor coluna, e as componentes covariantes
com um vetor linha, de modo que
AiBi =
A1B1 +
A2B2 +
... +
AnBn

Próxima: Schwarzschild
Volta: Interiores Estelares
Anterior: Relatividade Geral
 Astronomia e Astrofísica
Astronomia e Astrofísica
©
Modificada em 9 out 2011
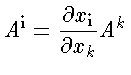
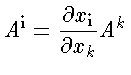
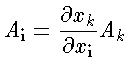
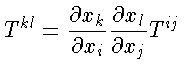
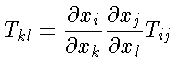
![]()