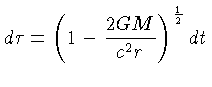Próxima: Tolman-Oppenheimer-Volkoff
Volta: Equilíbrio Hidrostático na Relatividade Geral
 Karl Schwarzschild (1873-1916)
estudou em 1916 o espaço em volta
da estrela, onde o tensor momentum-energia
Karl Schwarzschild (1873-1916)
estudou em 1916 o espaço em volta
da estrela, onde o tensor momentum-energia 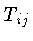 é nulo.
Neste caso, a equação de Einstein se reduz a:
é nulo.
Neste caso, a equação de Einstein se reduz a:
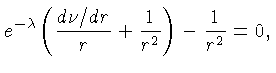 |
(1.94) |
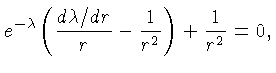 |
(1.95) |
e
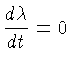 |
(1.96) |
Das equações (1.94) e (1.95) obtemos:
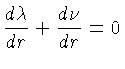 |
(1.97) |
Esta equação indica que podemos colocar
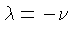 ,
e integrar, obtendo:
,
e integrar, obtendo:
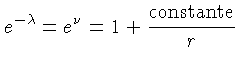 |
(1.98) |
Para que no limite no caso de campo gravitacional fraco
a equação de campo de Einstein se reduza à
equação de Poisson, a
 da
equação (1.98) deve ser identificada com
da
equação (1.98) deve ser identificada com 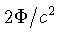 ,
onde
,
onde
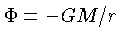 é o potencial gravitacional da mecânica clássica.
Note que M é a massa total do sistema, como no caso Newtoniano.
Com este valor, a métrica se reduz a:
é o potencial gravitacional da mecânica clássica.
Note que M é a massa total do sistema, como no caso Newtoniano.
Com este valor, a métrica se reduz a:
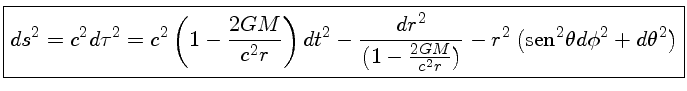 |
(1.99) |
conhecida como a métrica de Schwarzschild, e que tem
um horizonte de eventos no raio de Schwarzschild 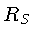 O raio de Schwarzschild não é uma singularidade,
pois pode ser removido com uma transformação de coordenadas.
O raio de Schwarzschild não é uma singularidade,
pois pode ser removido com uma transformação de coordenadas.
A distância propria nesta métrica pode ser estimada por:
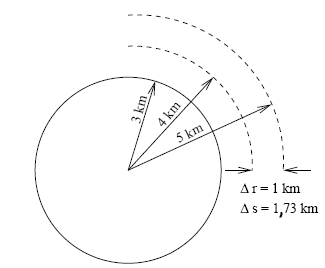
Para a massa do Sol, o raio de Schwarzschild é de 3 km,
e a distância própria entre r=4 km e r=5 km é
Deste modo, se construirmos uma barra rígida com comprimento de
1,7 km em uma estação espacial muito distante desta massa, veremos que esta
barra caberá entre 4 e 5 km [Edward Lewis Robinson (1945-), Black Holes].
Pela equação (1.99),
vemos que o intervalo de tempo da coordenada tempo 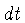 e o intervalo de tempo
próprio estão relacionados pela equação
e o intervalo de tempo
próprio estão relacionados pela equação
O intervalo de tempo próprio 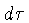 representa o intervalo
de tempo medido em um sistema em repouso na coordenada r.
Para um observador estacionário (dr=dθ=dφ=0) no infinito
(
representa o intervalo
de tempo medido em um sistema em repouso na coordenada r.
Para um observador estacionário (dr=dθ=dφ=0) no infinito
(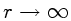 ),
o tempo próprio coincide com t.
),
o tempo próprio coincide com t.





Próxima: Avermelhamento Gravitacional
Próxima: Tolman-Oppenheimer-Volkoff
Volta: Equilíbrio Hidrostático na Relatividade Geral
©
Modificada em 6 Jul 2009
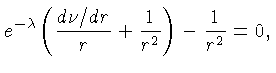
 Karl Schwarzschild (1873-1916)
estudou em 1916 o espaço em volta
da estrela, onde o tensor momentum-energia
Karl Schwarzschild (1873-1916)
estudou em 1916 o espaço em volta
da estrela, onde o tensor momentum-energia 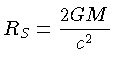
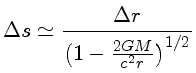
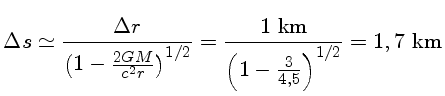
![]() e o intervalo de tempo
próprio estão relacionados pela equação
e o intervalo de tempo
próprio estão relacionados pela equação