Em nosso tratamento dos férmions, estamos escrevendo
 isto é, estamos identificando o potencial químico com a energia de Fermi.
Estamos também escrevendo a densidade de partículas como
isto é, estamos identificando o potencial químico com a energia de Fermi.
Estamos também escrevendo a densidade de partículas como 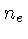 , isto é, a
densidade dos elétrons, pois os íons não estão
degenerados, exceto em estrelas de nêutrons. O valor da energia
de Fermi precisa ser encontrado através da integração da
distribuição de momentum, mas como vimos, no caso geral esta
integração não é analítica. Podemos estimar o
valor da energia de Fermi em várias aproximações:
O número de ocupação
o que leva a
Para
, isto é, a
densidade dos elétrons, pois os íons não estão
degenerados, exceto em estrelas de nêutrons. O valor da energia
de Fermi precisa ser encontrado através da integração da
distribuição de momentum, mas como vimos, no caso geral esta
integração não é analítica. Podemos estimar o
valor da energia de Fermi em várias aproximações:
O número de ocupação
o que leva a
Para
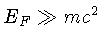 :
:
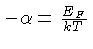 |
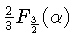 |
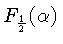 |
|
| -4 |
0,016179 |
0,016128 |
regime não degenerado |
| -2 |
0,117200 |
0,114588 |
|
| -1 |
0,307232 |
0,290501 |
|
| 0 |
0,768536 |
0,678094 |
|
| 1 |
1,774455 |
1,396375 |
|
| 2 |
3,691502 |
2,502458 |
|
| 4 |
11,751801 |
5,770726 |
|
| 8 |
52,90173 |
15,38048 |
|
| 12 |
125,70797 |
27,95178 |
|
| 16 |
279,63888 |
42,87300 |
|
| 20 |
484,37885 |
59,81279 |
completamente degenerado |
Em metais aqui na Terra, a energia de Fermi dos elétrons é
da ordem de alguns eV, enquanto a energia térmica correspondente
a 1000K é somente de 0,1 eV. Logo a energia dos elétrons
nos metais normais está limitada à energia de Fermi.
Nestas condições, a potencial químico e a
energia de Fermi são essencialmente equivalentes. Na
fórmula da distribuição de Fermi-Dirac,
é o potencial químico que aparece.
 Interiores Estelares
Interiores Estelares
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 15 março 2006
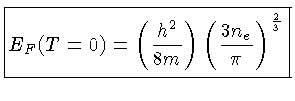
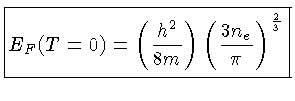
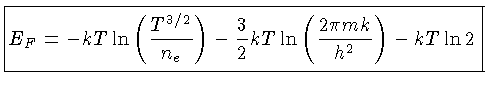
![$P(p)=\frac{1}{e^{(E-E_F)/kT}+1}=\frac{1}{e^{(E-E_F)/kT}\left[1+e^{-(E-E_F)/kT}\right]}$](img5.gif)
![$P(p)\simeq e^{-(E-E_F)/kT}\left[1-e^{-(E-E_F)/kT}\right]$](img6.gif)
![$n_e = \frac{2(2\pi mkT)^{3/2}}{h^3}e^{E_F/kT}(1-\frac{e^{E_...(2\pi mkT)^{3/2}}{h^3}e^{E_F/kT}[1-\frac{e^{E_F(T=0)/kT}}{2^{3/2}}]$](img7.gif)
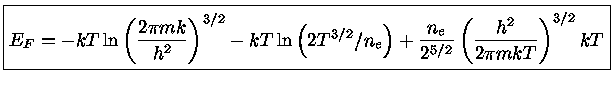
![${\frac{1}{E_F} = \frac{1}{E_F(T=0)}[1+\pi^2(\frac{kT}{E_F})^2]^\frac{1}{3}}$](img10.gif)
![]() Interiores Estelares
Interiores Estelares![]() Astronomia e Astrofísica
Astronomia e Astrofísica![]()