




Próxima: Energia Nuclear
Volta: Reserva de Energia de uma Estrela
Anterior: Reserva de Energia de uma Estrela
Algumas Relações Termodinâmicas
Seja uma variação infinitesimal de calor 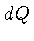 . A primeira
lei da termodinâmica é normalmente escrita como:
. A primeira
lei da termodinâmica é normalmente escrita como:
S
é a
entropia,
definida por Rudolf Julius Emanuel Clausius (1822-1888),
em 1865, como uma medida da desordem do sistema.
A entropia mede o número de microestados equivalentes para um mesmo macroestado de um sistema.
Um sistema em equilíbrio termodinâmico,
isto é, em equilíbrio mecânico e com
todas as partículas representadas pela mesma temperatura,
está em balanço detalhado, isto é, todos os
processos são balançados exatamente por processos inversos.
Esse sistema, em equilíbrio termodinâmico real não
irradia, e tem a entropia máxima.
Matematicamente, a entropia é definida como o logarítmo do
número de estados possíveis vezes a constante de
Boltzmann.
A função
ET, que escreveremos como E, é chamada de energia interna do sistema.
Podemos escrever a primeira lei também como
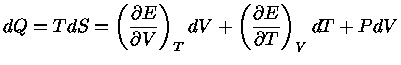 |
(1.32a) |
ou seja
![$dQ = TdS = [(\frac{\partial E}{\partial V})_T+P]dV+ (\frac{\partial E}{\partial T})_VdT$](imgrt3.gif) |
(1.32b) |
Exatidão
A primeira lei foi escrita da forma
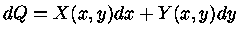 |
(1.32c) |
Se dQ é exato, isto é, pode ser escrita da forma geral
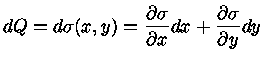 |
(1.32d) |
então, comparando com a equação (1.32c), podemos identificar
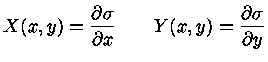 |
(1.32e) |
e se
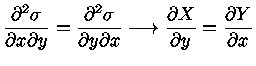 |
(1.32f) |
a diferencial
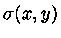 é exata e sua
integral independe do caminho de integração.
A energia interna de um sistema E
e a entropia S são
funções somente das variáveis do sistema, isto é,
são exatas, mas a integral de
é exata e sua
integral independe do caminho de integração.
A energia interna de um sistema E
e a entropia S são
funções somente das variáveis do sistema, isto é,
são exatas, mas a integral de  depende da
maneira em que o processo é executado.
depende da
maneira em que o processo é executado.
Relação de reciprocidade
Se um sistema está em equilíbrio
termodinâmico,
sua entropia é máxima e, portanto,
uma mudança infinitesimal no sistema tem de ser
quase-estática, ou reversível
e, portanto, com 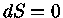 .
.
Da equação (1.32b) vemos que
![dS = \frac{dQ}{T} = \frac{1}{T}[(\frac{\partial E}...)_T+P]dV+ \frac{1}{T}(\frac{\partial E}{\partial T})_VdT](imgrt11.gif) |
(1.32g) |
Como 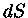 é exata, usando a relação (1.32f) obtemos
é exata, usando a relação (1.32f) obtemos
![\frac{\partial}{\partial T}{ \frac{1}{T}[\frac{...\partial V}[ \frac{1}{T}(\frac{\partial E}{\partial T}\right)_V]](imgrt13.gif) |
(1.32h) |
que, após a diferenciação, se reduz a:
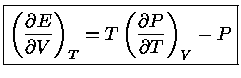 |
(1.32i) |
que nos dá a dependência da energia interna 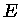 com
o volume, para temperatura constante.
com
o volume, para temperatura constante.
Caso Geral
Mas, no caso geral, em que existe alteração
nos constituintes do gás:
já que a energia total 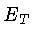 inclui todos os tipos relevantes de energia,
inclusive a energia latente das reações químicas,
que no nosso caso inclui reações nucleares.
Como
onde
inclui todos os tipos relevantes de energia,
inclusive a energia latente das reações químicas,
que no nosso caso inclui reações nucleares.
Como
onde 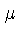 é o potencial químico
e a primeira
lei da termodinâmica deve ser escrita como:
A condição de equilíbrio químico (e a de equilíbrio
termodinâmico) requer
é o potencial químico
e a primeira
lei da termodinâmica deve ser escrita como:
A condição de equilíbrio químico (e a de equilíbrio
termodinâmico) requer
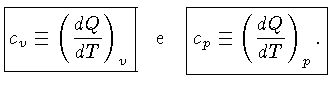
Calores Específicos
Os calores específicos a volume
constante 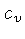 , e a pressão constante,
, e a pressão constante, 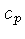 , por unidade de massa, são
definidos como:
, por unidade de massa, são
definidos como:
Se
onde 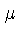 aqui é o peso molecular médio,
e
aqui é o peso molecular médio,
e
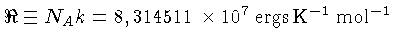 = 8,314511 J K-1mol-1
é a constante universal do gás por mol,
= 8,314511 J K-1mol-1
é a constante universal do gás por mol,
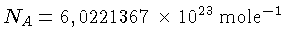 é o número de Avogadro e a lei
do gás ideal é expressa como
é o número de Avogadro e a lei
do gás ideal é expressa como
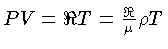 .
.
Se as partículas são consideradas como pontuais, só possuem
três graus de liberdade e, para os casos não relativístico
(N.R.) e extremamente relativístico (E.R.), a
energia térmica, por partícula, é dada por
[equações (1.9b)
e (1.9h)]:
e por unidade de massa:
onde 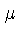 aqui é o peso molecular médio.
Como
obtemos
e como
aqui é o peso molecular médio.
Como
obtemos
e como
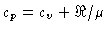 ,
e
Uma relação adiabática é definida como:
Definindo-se também:
,
e
Uma relação adiabática é definida como:
Definindo-se também:
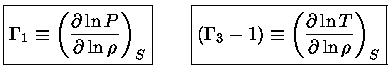 |
(1.32-1) |
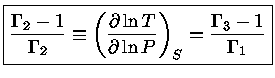 |
(1.32-2) |
e o expoentes na equação de estado:
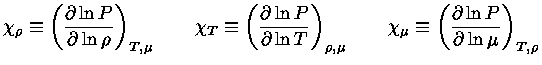 |
(1.32-3) |
onde
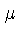 é o peso molecular.
é o peso molecular.
Pelas definições dos expoentes, e assumindo-se equilíbrio
químico, isto é, peso molecular constante 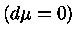 :
:
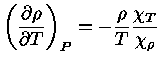 |
(1.32-4) |
Como,
usando a regra da derivação em cadeia:
![$ dE = (\frac{\partial E}{\partial P})_T [(\fr...
...rtial T})_\rho dT] + (\frac{\partial E}{\partial T})_PdT$](rt/img6.gif) |
(1.32-5) |
ou seja, se 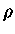 é constante:
é constante:
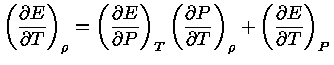 |
(1.32-6) |
de onde obtemos:
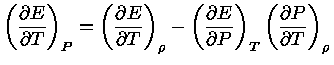 |
(1.32-7) |
Sabemos que, em equilíbrio químico,
a primeira lei pode ser escrita
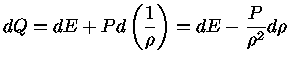 |
(1.32-8) |
podemos obter
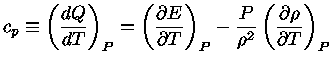 |
(1.32-9) |
podemos usar a equação (1.32-4) para escrever a equação
(1.32-9) como:
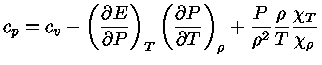 |
(1.32-10) |
que também pode ser escrito como
Podemos, finalmente, utilizar a relação de
reciprocidade (equação 1.32i)
para escrever
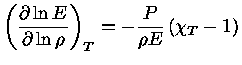 |
(1.32-12) |
e obter a relação geral entre os calores específicos:
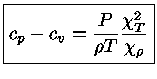 |
(1.32-13) |
Como para um gás ideal
obtemos que
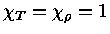 e
e
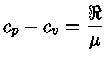 |
(1.32-14) |
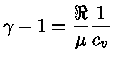 |
(1.32-15) |
e como
obtemos que para composição química constante:
e usando
obtemos
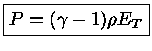 |
(1.32-16) |
No caso geral
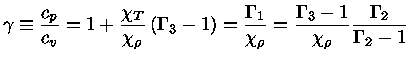 |
(1.32-17) |
e como
uma expansão adiabática terá:
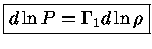 |
(1.32-18) |
A unidade de calor é chamada Carnot (Ct), em honra
ao físico francês Sadi Nicolas Lionard Carnot (1796-1832).
1 Ct = 1 Joule/Kelvin é a quantidade de calor necessário
para derreter um centímetro cúbico de gelo.
O conceito de entropia está intimamente ligado ao
conceito de calor. Quando um sistema recebe entropia (calor),
ele recebe energia.
Se um corpo a uma temperatura T recebe entropia (S), ele
absorve energia (E) equivalente ao produto da temperatura
pela entropia.
A entropia (calor) pode ser transportada, armazenada e criada.
A entropia é o transportador da
energia em processos térmicos. Ela pode ser criada
em processos irreversíveis, como queima, frição,
transporte de calor, mas não pode ser destruída.
A quantidade de energia usada na criação de entropia
é dita dissipada.
A relação entre a entropia macroscópica de Rudolf
Clausius e os estados microscópicos de um sistema
foi feita pelo físico
austríaco Ludwig Boltzmann (1844-1906),
com sua teoria estatística de não equilíbrio,
irreversível e não simétrica no tempo. Cada estado
microscópico de um sistema macroscópico tem uma
entropia definida por
onde
|
k = constante de Boltzmann = 1,38×10-23
J K-1 |
|
e W é o volume do espaço de fases associado ao estado
macroscópico,
isto é, o número de possíveis estados microscópicos
associados a um estado macroscópico
(número de estados com mesma
energia e portanto igualmente acessíveis).
A entropia aumenta quando o espaço de fases aumenta.
Para a água, a 20C, CV=4180 J K-1 kg-1
enquanto CP=4196,4 J K-1 kg-1.
Para a água (vapor), a 100C, CV=1463 J K-1 kg-1
enquanto CP=1952 J K-1 kg-1.
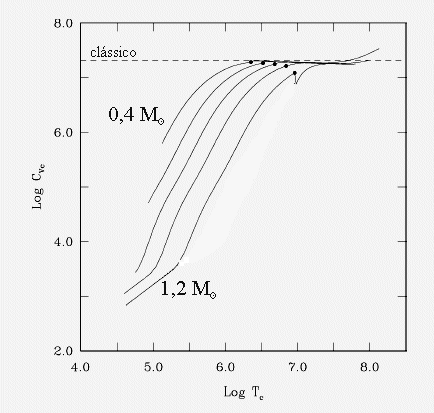
Calor específico a volume constante dos elétrons no núcleo de estrelas anãs brancas,
de acordo com os cálculos de Gilles Fontaine, Pierre Brassard e
Pierre Bergeron, da Université de Montréal, no Canadá, publicados
em 2001 no Publications of the Astronomical Society of the Pacific,
113, 409. A linha tracejada indica o valor clássico de um sólido
de carbono. Os modelos são para anãs brancas com massas de 0,4,
0,6, 0,8, 1,0 e 1,2 massas solares. Os pontos marcam o início da
cristalização.
Para um gás de fótons ocupando um volume V, 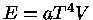 e
e
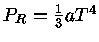 . Deste modo
de modo que
mas
A relação entre a pressão (ou energia)
e a densidade da matéria é normalmente conhecida
com a Equação de Estado do sistema.
Alexander
Yurievich Potekhin,
Gilles Chabrier
& Forrest J. Rogers
publicaram em 2008, "Equation of state of classical Coulomb plasma mixtures",
no Physical Review E.
. Deste modo
de modo que
mas
A relação entre a pressão (ou energia)
e a densidade da matéria é normalmente conhecida
com a Equação de Estado do sistema.
Alexander
Yurievich Potekhin,
Gilles Chabrier
& Forrest J. Rogers
publicaram em 2008, "Equation of state of classical Coulomb plasma mixtures",
no Physical Review E.
O estado inicial do Universo tinha menor entropia e,
portanto, o físico
americano Richard Philips Feynman (1918-1988) propôs que "é preciso
adicionar às leis físicas a hipótese de que o Universo
era mais ordenado, em um sentido técnico, no passado do que
é atualmente ... para dar sentido à irreversibilidade".
O físico brasileiro Constantino Tsallis propõe uma
mecânica estatística mais abrangente, que leva em conta
a impossibilidade de se separar completamente (isolar) sistemas
interagentes por forças de longo alcance, como gravitacionais
ou eletromagnéticas. Nesta teoria, a entropia não é
simplesmente aditiva.
A entropia em um ponto pode ser calculada usando-se
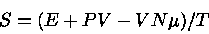 |
(1) |
usando-se 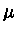 como o potencial químico sem a massa de repouso
(
como o potencial químico sem a massa de repouso
(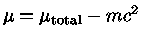 ) e
) e
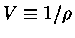 .
.
Para um gás de partículas extremamente relativísticas,
como fótons e neutrinos, em expansão adiabática, se assumirmos
que seu potencial químico é nulo, temos que a energia
por unidade de volume é dada por 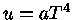 e
e
onde 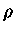 é a densidade. A entropia
de fótons por núcleon é dada por
é a densidade. A entropia
de fótons por núcleon é dada por
No núcleo de uma estrela de 25 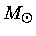 , esta razão
, esta razão
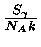 varia de 1 quando está
queimando o hidrogênio e o hélio, para 0,4 durante a queima do carbono,
chegando a 0,01 durante a queima do oxigênio e silício.
varia de 1 quando está
queimando o hidrogênio e o hélio, para 0,4 durante a queima do carbono,
chegando a 0,01 durante a queima do oxigênio e silício.
Para um gás de Fermi-Dirac não relativístico e não degenerado,
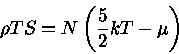 |
(2) |
Para um gás de elétrons degenerado
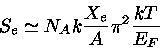 |
(3) |
Em um núcleo de
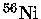 próximo do colapso,
próximo do colapso,
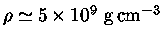 ,
,
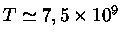 K,
K,
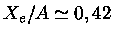 ,
, 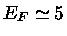 MeV,
MeV,
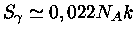 ,
,
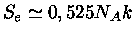 e
e
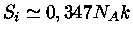 , de modo que
, de modo que
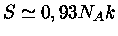 . A entropia não se altera
muito durante o colapso.
. A entropia não se altera
muito durante o colapso.





Próxima: Energia Nuclear
Volta: Reserva de Energia de uma Estrela
Anterior: Reserva de Energia de uma Estrela
©
Modificada em 31 dez 2008
![]() . A primeira
lei da termodinâmica é normalmente escrita como:
. A primeira
lei da termodinâmica é normalmente escrita como:
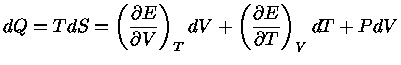
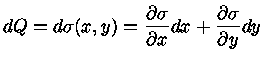
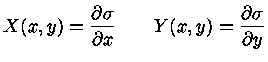
![]() .
.
![dS = \frac{dQ}{T} = \frac{1}{T}[(\frac{\partial E}...)_T+P]dV+ \frac{1}{T}(\frac{\partial E}{\partial T})_VdT](imgrt11.gif)
![\frac{\partial}{\partial T}{ \frac{1}{T}[\frac{...\partial V}[ \frac{1}{T}(\frac{\partial E}{\partial T}\right)_V]](imgrt13.gif)
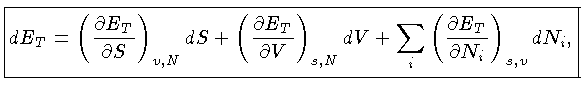
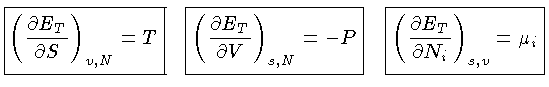
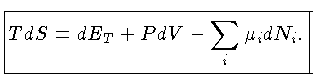
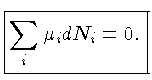
![]() , e a pressão constante,
, e a pressão constante, ![]() , por unidade de massa, são
definidos como:
, por unidade de massa, são
definidos como:
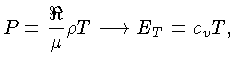
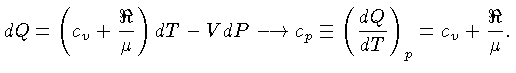
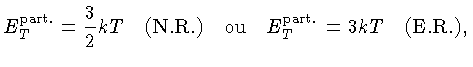
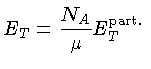
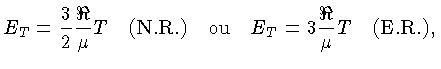
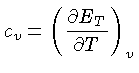
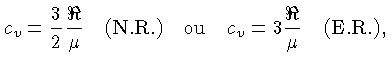
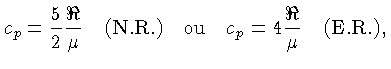
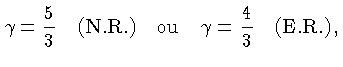
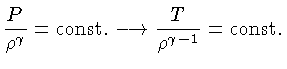
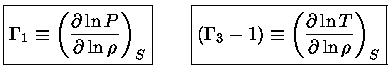
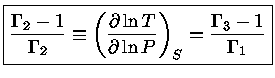
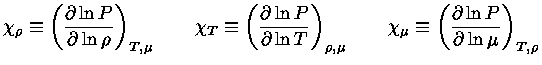
![]() :
:
![$ dE = (\frac{\partial E}{\partial P})_T [(\fr...
...rtial T})_\rho dT] + (\frac{\partial E}{\partial T})_PdT$](rt/img6.gif)
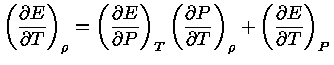
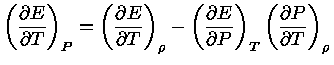
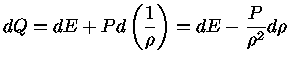
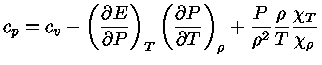
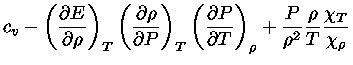
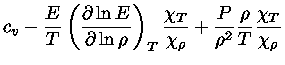
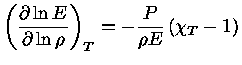
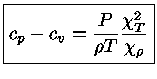
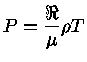
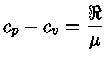
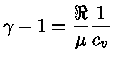
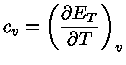
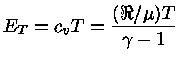
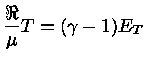
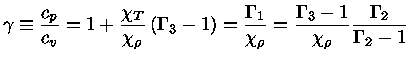
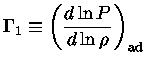

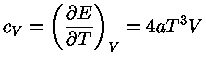
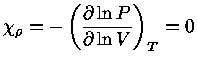
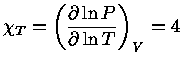
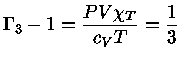
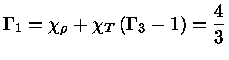
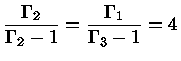
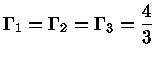
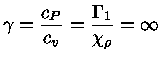
![]() e
e
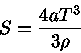
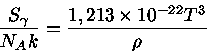
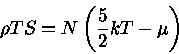
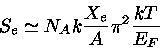
![]() próximo do colapso,
próximo do colapso,
![]() ,
,
![]() K,
K,
![]() ,
, ![]() MeV,
MeV,
![]() ,
,
![]() e
e
![]() , de modo que
, de modo que
![]() . A entropia não se altera
muito durante o colapso.
. A entropia não se altera
muito durante o colapso.