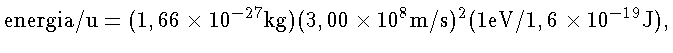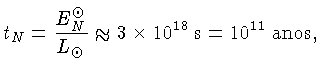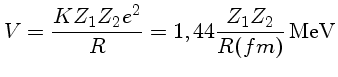Próxima: Condição de Equilíbrio Térmico
Volta: Reserva de Energia de uma Estrela
Anterior: Algumas Relações Termodinâmicas
O último tipo de reserva de energia é a nuclear.
A temperatura no interior das estrelas é alta o suficiente para manter
fusão nuclear de elementos leves.
 Reações nucleares
liberam energia proveniente do equivalente de massa dos núcleos
envolvidos. Poder-se-ia supor que a energia nuclear total de uma
estrela fosse
Reações nucleares
liberam energia proveniente do equivalente de massa dos núcleos
envolvidos. Poder-se-ia supor que a energia nuclear total de uma
estrela fosse
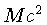 , mas esta é uma super-estimativa, pois esta
energia somente seria irradiada se a estrela fosse totalmente
aniquilada. Esta aniquilação não ocorre às temperaturas
encontradas nas estrelas. Portanto somente precisamos considerar
reações nucleares que transmutam um elemento químico
em outro. A energia liberada nestes processos é equivalente
à diferença de massa, que é muito menor do que a massa
total dos núcleons,
como estudado por Hans Albrecht Bethe (1906-2005)
no seu artigo A Produção de Energia nas Estrelas,
de 1939, e que lhe valeu o prêmio Nobel em 1967,
, mas esta é uma super-estimativa, pois esta
energia somente seria irradiada se a estrela fosse totalmente
aniquilada. Esta aniquilação não ocorre às temperaturas
encontradas nas estrelas. Portanto somente precisamos considerar
reações nucleares que transmutam um elemento químico
em outro. A energia liberada nestes processos é equivalente
à diferença de massa, que é muito menor do que a massa
total dos núcleons,
como estudado por Hans Albrecht Bethe (1906-2005)
no seu artigo A Produção de Energia nas Estrelas,
de 1939, e que lhe valeu o prêmio Nobel em 1967,
Combinando um
próton (p) e um nêutron (n) produzirá um deutério (d).
Se adicionarmos a massa do próton e do nêutron, obtemos
Como a massa do deutério é
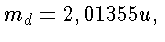 a diferença de massa é dada por:
Uma unidade de massa atômica (UMA=u)
é, por definição, igual a 1/12 da massa do
átomo de
a diferença de massa é dada por:
Uma unidade de massa atômica (UMA=u)
é, por definição, igual a 1/12 da massa do
átomo de 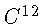 , correspondendo a
, correspondendo a
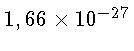 kg. Desta forma, usando
kg. Desta forma, usando 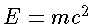 ,
nos dá
correspondendo a
931 MeV/u. Logo, a energia liberada na formação do
deutério é
Portanto 2,24 MeV é a energia total de
ligação do deutério.
,
nos dá
correspondendo a
931 MeV/u. Logo, a energia liberada na formação do
deutério é
Portanto 2,24 MeV é a energia total de
ligação do deutério.
m(41H)=1,0073 M(4He),
m(34He)=1,00065 M(12C), ...,
m(561H)=1,0091 M(56Fe),
usando M(H)=1,00794 u.m.a. e
M(56Fe)=55,9349375 u.m.a..
Quando excluimos do cálculo a massa dos elétrons, que não são
transformados nas reações nucleares, obtemos que somente 0,008 da
massa é transformada, desde H a Fe.
A máxima diferença de massa ocorre
na transmutação de hidrogênio em ferro, e corresponde
a oito milésimos da massa dos núcleons envolvidos no processo.
Será que a reserva de energia nuclear em uma estrela se aproxima
deste máximo teórico? Sim. Evidências espectroscópicas
indicam que a maioria das estrelas é composta principalmente de
hidrogênio, o combustível mais vantajoso para as estrelas.
E, como produto final, pouca diferença faz se o hidrogênio
é transformado em ferro, já que a transmutação
em hélio libera uma diferença de massa de sete milésimos.
Deste modo, o limite teórico dá uma boa aproximação
da reserva de energia nuclear de uma estrela. Para o Sol,
obtemos:
que é mais de mil vezes superior às energias
térmica e gravitacional. Para o Sol, esta reserva
de energia pode suprir a perda por radiação por
um intervalo de tempo de:
suficientemente longo. Eventualmente, a transmutação
gradual dos elementos por fusão causa mudanças
significativas na estrutura da estrela.
Para que uma reação nuclear ocorra, as partículas
precisam vencer a barreira Coulombiana
[Charles Augustin de Coulomb (1736-1806)]
repulsiva entre as
partículas, dada por
onde 1 fermi (fentometro) equivale a 10-15m,
enquanto que a energia cinética entre as partículas
é determinada por uma distribuição de velocidades de
Maxwell-Boltzmann correspondente à energia térmica
A temperatura no núcleo do Sol é da ordem de 15 milhões de K,
e para estrelas mais massivas, da ordem de 500 milhões de K.
A energia média das partículas
interagentes,
de 1,2 a 43 keV,
é muitas ordens de magnitudes menor
do que a barreira Coulombiana que as separa. As reações ocorrem pelo
efeito de tunelamento quântico, proposto em 1928
pelo físico russo-americano George Antonovich Gamow (1904-1968).
As partículas
com maior chance de penetrar a barreira são aquelas com
a máxima energia na distribuição de Maxwell-Boltzmann.





Próxima: Reações Nucleares
Volta: Reserva de Energia de uma Estrela
Anterior: Algumas Relações Termodinâmicas
©
Modificada em 16 ago 2011
 Reações nucleares
liberam energia proveniente do equivalente de massa dos núcleos
envolvidos. Poder-se-ia supor que a energia nuclear total de uma
estrela fosse
Reações nucleares
liberam energia proveniente do equivalente de massa dos núcleos
envolvidos. Poder-se-ia supor que a energia nuclear total de uma
estrela fosse
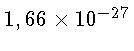 kg. Desta forma, usando
kg. Desta forma, usando