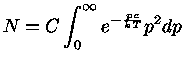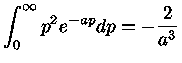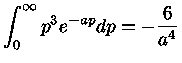Próxima: Gás de Fótons
Volta: Pressão Mecânica
Anterior: Pressão Mecânica
Para um gás monoatômico perfeito e não degenerado,
nem relativístico, a distribuição de momentum
em equilíbrio térmico é dada pela
Lei de Maxwell [James Clerk Maxwell (1831-1879)].
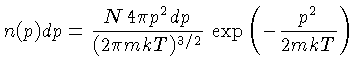 |
(1.8) |
onde 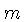 é a massa da partícula,
é a massa da partícula, 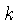 é a
constante de Boltzmann, e
é a
constante de Boltzmann, e 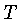 a temperatura do gás.
a temperatura do gás.
Note que a normalização é escolhida de forma que
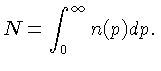 |
(1.9) |
Integrando-se a equação (1.7), usando a Lei de Maxwell (1.8),
a normalização (1.9), e 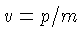 , obtém-se:
, obtém-se:
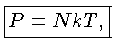
| (1.9a) |
a equação de um gás ideal.
A densidade de energia 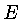 , de acordo com a equação (1.5), para um gás ideal é dada por:
, de acordo com a equação (1.5), para um gás ideal é dada por:
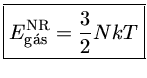
| (1.9b) |
Para o gás de Boltzmann, o potencial químico, incluindo a energia de repouso, é dado por:
onde g=2J+1
é o fator estatístico para partículas de spin J.
Para um gás ultra-relativístico,
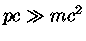 ,
a energia da partícula é dada por
,
a energia da partícula é dada por
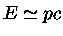 ,
e usando a equação (1.9) para obter a
constante normalização
,
e usando a equação (1.9) para obter a
constante normalização 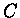 :
:
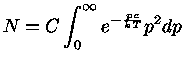
| (1.9c) |
Como
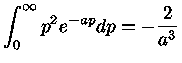 |
(1.9d) |
obtemos
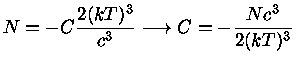 |
(1.9e) |
e, portanto, a energia do gás é dada por
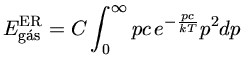 |
(1.9f) |
Como
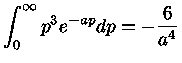 |
(1.9g) |
a equação (1.9f) se reduz a
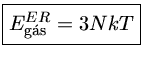 |
(1.9h) |





Próxima: Gás de Fótons
Volta: Pressão Mecânica
Anterior: Pressão Mecânica
©
Modificada em 3 jan 2002
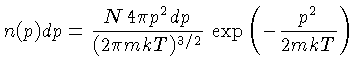
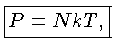
![]() , de acordo com a equação (1.5), para um gás ideal é dada por:
, de acordo com a equação (1.5), para um gás ideal é dada por:
![\mu = mc^2 + kT \ln [\frac{N}{g}(\frac{h^2}{2\pi mkT})^\frac{3}{2}]](imgmu1.gif)
![]() ,
a energia da partícula é dada por
,
a energia da partícula é dada por
![]() ,
e usando a equação (1.9) para obter a
constante normalização
,
e usando a equação (1.9) para obter a
constante normalização ![]() :
: