




Próxima: Equilíbrio Convectivo
Volta: Transporte de Energia por Convecção
Anterior: Transporte de Energia por Convecção
Consideremos a seguinte perturbação: tomemos um pequeno elemento
de volume no interior da estrela. Desloquemos este elemento de matéria
para cima, por uma distância dr.
Deixemos que o elemento se expanda adiabaticamente (sem perda de calor)
até que a pressão dentro do elemento de volume seja igual
à pressão do meio que o circunda. Soltemos este elemento para
verificar se ele volta para baixo, até sua posição inicial,
ou se ele continua a se mover para cima. Se ele retorna à
posição inicial, a camada está em equilíbrio radiativo
estável; a radiação é suficiente para
manter o transporte de energia. Se ele continua a se mover para cima, o equilíbrio radiativo
é instável, e movimentos de convecção persistem.
Em maior detalhe, usemos a nomenclatura da figura anterior:
as quantidades do interior do elemento são
designadas por asterístico, enquanto as
quantidades do meio não perturbado não têm
asterístico. O subscrito 1 se refere à
posição original, enquanto o subscrito 2 se refere
à posição mais alta para a qual o elemento foi elevado.
Antes de começarmos a perturbação, o elemento
em consideração tem as mesmas propriedades do meio
que o cerca, de modo que:
Depois do deslocamento, a pressão está novamente em
equilíbrio com o meio circundante, mas a densidade interna
estará determinada pela
expansão adiabática do elemento
(dlnP = Γ1 dlnρ), pois estamos assumindo que a
bolha não perde calor durante o deslocamento.
Desta forma, temos:
onde 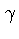 é o
coeficiente de expansão adiabática,
assumindo
é o
coeficiente de expansão adiabática,
assumindo 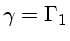 ,
igual à razão dos calores específicos a pressão
constante e a volume constante, e tem valor de 5/3 para
um gás altamente ionizado ou ideal.
,
igual à razão dos calores específicos a pressão
constante e a volume constante, e tem valor de 5/3 para
um gás altamente ionizado ou ideal.
A força de pressão exercida sobre o volume após
seu deslocamento não foi alterada pela perturbação.
A força gravitacional sobre o mesmo elemento,
entretanto, foi alterada se a densidade dentro do elemento
for diferente da densidade do meio. Especificamente, se a densidade
interna for maior do que a do meio, a força
gravitacional será maior, e o elemento sofrerá
uma força resultante para baixo, voltando à
sua posição inicial. Portanto, sob a condição:
qualquer perturbação será imediatamente contrabalançada,
e a camada será completamente estável.
Esta condição de estabilidade pode ser transformada em
uma forma mais conveniente. As quantidades na posição
mais alta (subscrito 2) podem ser expressas
em termos das quantidades e
suas derivadas na posição inicial
(subscrito 1).
Como:
No limite de variações infinitesimais:
Logo:
ou
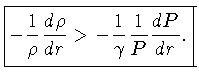 |
(1.52) |
Esta inequalidade é uma forma exata e geral da condição
de equilíbrio contra movimentos convectivos em qualquer
camada da estrela. Se o módulo do gradiente de densidade real
for maior do que o módulo do gradiente de densidade adiabático,
não ocorrem movimentos convectivos.
Para o caso de uma equação de estado de gás ideal (1.25),
esta condição pode ser escrita, para o
caso em que o peso molecular μ
é constante, como:
ou
de modo que a condição de estabilidade (1.52) para um gás ideal pode ser escrita como:
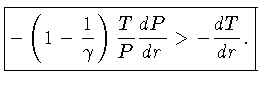 |
(1.53) |
Como o gradiente de pressão e o gradiente de temperatura são sempre
negativos, os dois lados da equação contém quantidades positivas.
O lado direito da equação contém o verdadeiro gradiente
de temperatura na camada. O lado esquerdo é normalmente
chamado de
gradiente de temperatura adiabático,
já que ele representa o gradiente de temperatura se
a pressão e a temperatura seguissem uma relação
adiabática. A condição (1.53) significa dizer
que a camada será estável se o gradiente de temperatura
real, em valor absoluto, for menor do que o gradiente de temperatura
adiabático.
As condições de estabilidade (1.52) e (1.53)
não podem ser aplicadas, sem considerações especiais,
para camadas com composição química diferentes.
A condição
(1.53) é chamada de
condição de estabilidade de Schwarzschild, ou
critério de Schwarzschild,
desenvolvida por Karl Schwarzschild (1873-1916) em 1906.
Note que esta condição não leva em conta a possibilidade de
mudança de composição entre as duas camadas. Um
critério semelhante, levando-se em conta a possibilidade de
mudança do peso molecular
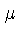 dentro da bolha em relação ao meio,
e definindo:
dentro da bolha em relação ao meio,
e definindo:
os coeficientes da equação de estado
chama-se critério de Ledoux,
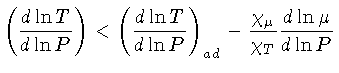 |
(1.54) |
 proposto pelo belga
Paul Ledoux (1914-1988).
Neste caso, um peso molecular
proposto pelo belga
Paul Ledoux (1914-1988).
Neste caso, um peso molecular 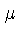 que aumenta para dentro, como normalmente
ocorre em estrelas evoluídas, tende a estabilizar a região
contra convecção, pois neste caso
que aumenta para dentro, como normalmente
ocorre em estrelas evoluídas, tende a estabilizar a região
contra convecção, pois neste caso
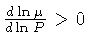 .
.
Usando a nomenclatura dos deltas,
o critério de Schwarzschild para que haja convecção
(1.53) pode ser escrito como:
e a relação (1.54),
levando-se em conta a pressão de radiação,
e definindo
pode ser escrita como:
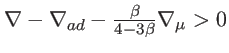
ou ∇ - ∇
Ledoux > 0
com
Como
para um gás ideal
Se assumirmos uma equação de gás ideal para o gás, e
definirmos 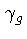 como o coeficiente para o gás,
e a pressão total como a soma da pressão de radiação
mais pressão do gás, o coeficiente
como o coeficiente para o gás,
e a pressão total como a soma da pressão de radiação
mais pressão do gás, o coeficiente 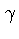 da
combinação pode ser escrito em termos da
razão da pressão do gás para a pressão total,
da
combinação pode ser escrito em termos da
razão da pressão do gás para a pressão total,
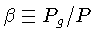 :
Richard B. Stothers & Chao-wen Chin, no artigo
A Clue to the Extent of Convective Mixing Inside Massive Stars:
The Surface Hydrogen Abundances of Luminous Blue Variables and Hydrogen-poor
Wolf-Rayet Stars,
(2000, Astrophysical Journal, 540, 1041), mostram que modelos calculados com
o critério de Schwarzschild concordam com as observações, enquanto
os calculados com o de Ledoux não concordam.
O artigo de 2014 de Arlette Noels, Melanie Godart, Sébastien J.A.J. Salmon, M. Grabriel,
J. Moltalban & Andrea Miglio, no Proceedings of the IAU Symposium 307, New windows on massive stars:
asteroseismology, interferometry and spectropolarimetry, Georges Meynet,
Cyril Georgy, José H. Groh & Philippe Stee, eds, mostra que
a detecção de mais frequências de pulsações nas estrelas, e sua comparação com modelos asterosismológicos, ajudará a resolver o problema.
:
Richard B. Stothers & Chao-wen Chin, no artigo
A Clue to the Extent of Convective Mixing Inside Massive Stars:
The Surface Hydrogen Abundances of Luminous Blue Variables and Hydrogen-poor
Wolf-Rayet Stars,
(2000, Astrophysical Journal, 540, 1041), mostram que modelos calculados com
o critério de Schwarzschild concordam com as observações, enquanto
os calculados com o de Ledoux não concordam.
O artigo de 2014 de Arlette Noels, Melanie Godart, Sébastien J.A.J. Salmon, M. Grabriel,
J. Moltalban & Andrea Miglio, no Proceedings of the IAU Symposium 307, New windows on massive stars:
asteroseismology, interferometry and spectropolarimetry, Georges Meynet,
Cyril Georgy, José H. Groh & Philippe Stee, eds, mostra que
a detecção de mais frequências de pulsações nas estrelas, e sua comparação com modelos asterosismológicos, ajudará a resolver o problema.
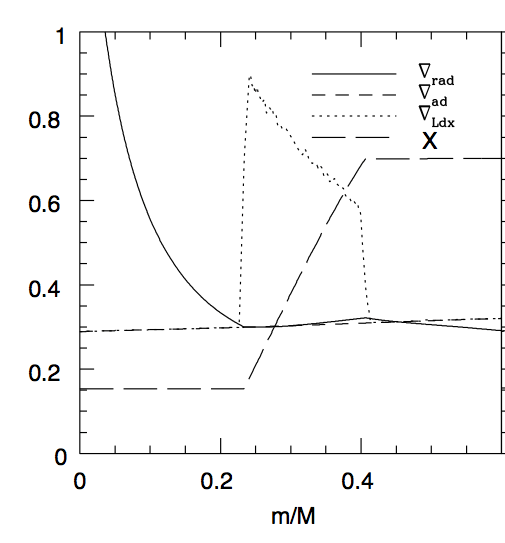
A linha tracejada longa mostra o perfil de hidrogênio (X) para um modelo de estrela com 16 massas solares na sequência principal,
a linha cheia o gradiente radiativo, a linha tracejada curta o gradiente adiabático, enquanto a linha
pontilhada mostra o gradiente de Ledoux. O núcleo convectivo deve ser calculado ∇
rad=∇
ad
no lado convectivo da borda.
Ao se construir um modelo de estrela, a condição de estabilidade
(1.53) precisa ser verificada em cada camada do modelo. Isto
é, o gradiente de pressão precisa ser computado usando-se
a condição de equilíbrio hidrostático (1.24),
o gradiente de temperatura precisa ser calculado usando-se
a equação do equilíbrio radiativo (1.51),
e seus valores inseridos na condição (1.53).
Se esta condição é satisfeita, a camada é estável,
e o equilíbrio radiativo se aplica. Mas e se a
condição (1.53) não for satisfeita?
Esta é a questão que precisamos agora considerar em detalhe.
Este problema tem consequências significativas nos modelos
estelares. Nos núcleos de estrelas, os fluxos de radiação
são consideráveis, e altas opacidades muitas vezes ocorrem.
De acordo com a condição de equilíbrio radiativo (1.51),
estas duas circunstâncias levam a altos - e portanto
instáveis - gradientes de temperatura.
Usando-se a equação de equilíbrio radiativo (1.51),
e a equação do equilíbrio hidrostático (1.24),
obtemos:
Como normalmente, embora não sempre, 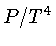 é uma
função que varia suavemente com a posição na estrela,
o início da convecção no núcleo da estrela é
determinado pelos valores da opacidade
é uma
função que varia suavemente com a posição na estrela,
o início da convecção no núcleo da estrela é
determinado pelos valores da opacidade 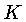 , e da razão
, e da razão
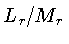 . Um valor alto da opacidade implica em um valor
alto do gradiente de temperatura, para que um dado valor
do fluxo seja transportado pela radiação. No núcleo
das estrelas, a opacidade geralmente decresce em direção
ao centro; este efeito dificulta o início da convecção.
A luminosidade
. Um valor alto da opacidade implica em um valor
alto do gradiente de temperatura, para que um dado valor
do fluxo seja transportado pela radiação. No núcleo
das estrelas, a opacidade geralmente decresce em direção
ao centro; este efeito dificulta o início da convecção.
A luminosidade 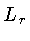 se mantém basicamente constante,
enquanto que a massa aumenta com o raio. Desta forma, em direção
ao centro,
se mantém basicamente constante,
enquanto que a massa aumenta com o raio. Desta forma, em direção
ao centro, 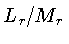 aumenta o suficiente em estrelas com
fontes de energia concentradas (estrelas mais massivas),
e estas estrelas terão núcleo convectivo.
aumenta o suficiente em estrelas com
fontes de energia concentradas (estrelas mais massivas),
e estas estrelas terão núcleo convectivo.
Nas camadas externas,
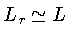 e
e
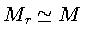 , e o
fator
, e o
fator 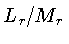 não mais determina o início da convecção.
Entretanto, o gradiente adiabático não é constante,
pois é muito sensível ao estado de ionização dos
constituintes dominantes, hidrogênio e hélio. Em uma
região de ionização parcial, o gradiente adiabático
torna-se muito pequeno, e uma zona de convecção se inicia.
Portanto, todas as estrelas que não são quentes o suficiente
para que o hidrogênio esteja completamente ionizado na
fotosfera, têm zonas de convecção próximas à
superfície.
não mais determina o início da convecção.
Entretanto, o gradiente adiabático não é constante,
pois é muito sensível ao estado de ionização dos
constituintes dominantes, hidrogênio e hélio. Em uma
região de ionização parcial, o gradiente adiabático
torna-se muito pequeno, e uma zona de convecção se inicia.
Portanto, todas as estrelas que não são quentes o suficiente
para que o hidrogênio esteja completamente ionizado na
fotosfera, têm zonas de convecção próximas à
superfície.
 As duas zonas de convecção superficiais em uma estrela A4V com
Tef=8 500 K e log g=4,13. Estas estrelas têm duas
zonas de convecção, a superior, próximo a 8 000K, devido à zona de ionização
parcial do H e primeira ionização do He e a inferior, próxima de 50 000 K,
devido à segunda
ionização do He. Albrecht Unsöld (1905-1995) publicou em 1930
no Zeitschrift für Astrophysik, 1, 138
(Konvektion in der Sonnenatmosphäre)
a descoberta de que as
zonas de ionização parcial têm importância fundamental na
existência e extensão das zonas de convecção.
As duas zonas de convecção superficiais em uma estrela A4V com
Tef=8 500 K e log g=4,13. Estas estrelas têm duas
zonas de convecção, a superior, próximo a 8 000K, devido à zona de ionização
parcial do H e primeira ionização do He e a inferior, próxima de 50 000 K,
devido à segunda
ionização do He. Albrecht Unsöld (1905-1995) publicou em 1930
no Zeitschrift für Astrophysik, 1, 138
(Konvektion in der Sonnenatmosphäre)
a descoberta de que as
zonas de ionização parcial têm importância fundamental na
existência e extensão das zonas de convecção.
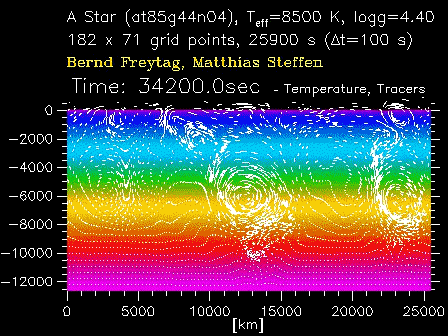 Simulação bi-dimensional da convecção para uma
estrela tipo A na seqüência principal,
de Hans-Günther Ludwig e Matthias Steffen
(1996, Astronomy & Astrophysics, 313, 497). No eixo y está mostrado
o negativo da temperatura, em K, em relação à superfície. A temperatura
cresce para dentro.
Simulação bi-dimensional da convecção para uma
estrela tipo A na seqüência principal,
de Hans-Günther Ludwig e Matthias Steffen
(1996, Astronomy & Astrophysics, 313, 497). No eixo y está mostrado
o negativo da temperatura, em K, em relação à superfície. A temperatura
cresce para dentro.





Próxima: Equilíbrio Convectivo
Volta: Transporte de Energia por Convecção
Anterior: Transporte de Energia por Convecção
©
Modificada em 8 set 2014
 Zona de convecção na fotosfera do Sol
Zona de convecção na fotosfera do Sol
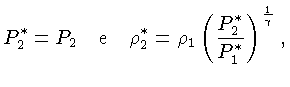
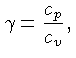
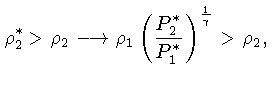
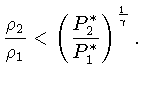
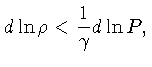
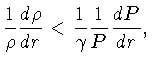
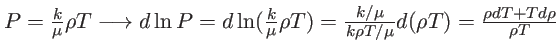
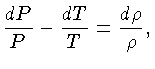
![]() dentro da bolha em relação ao meio,
e definindo:
dentro da bolha em relação ao meio,
e definindo:
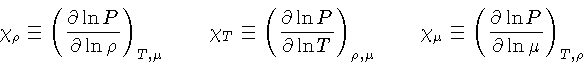
 proposto pelo belga
Paul Ledoux (1914-1988).
Neste caso, um peso molecular
proposto pelo belga
Paul Ledoux (1914-1988).
Neste caso, um peso molecular 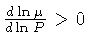 .
.
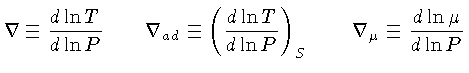
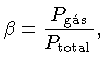
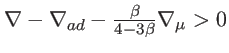 ou ∇ - ∇Ledoux > 0
ou ∇ - ∇Ledoux > 0
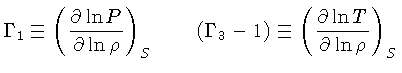
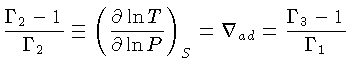
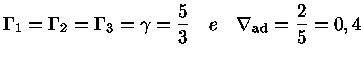
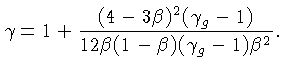

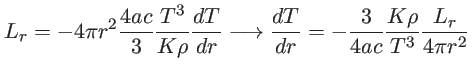
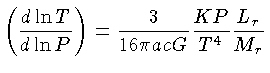
![]() e
e
![]() , e o
fator
, e o
fator ![]() não mais determina o início da convecção.
Entretanto, o gradiente adiabático não é constante,
pois é muito sensível ao estado de ionização dos
constituintes dominantes, hidrogênio e hélio. Em uma
região de ionização parcial, o gradiente adiabático
torna-se muito pequeno, e uma zona de convecção se inicia.
Portanto, todas as estrelas que não são quentes o suficiente
para que o hidrogênio esteja completamente ionizado na
fotosfera, têm zonas de convecção próximas à
superfície.
não mais determina o início da convecção.
Entretanto, o gradiente adiabático não é constante,
pois é muito sensível ao estado de ionização dos
constituintes dominantes, hidrogênio e hélio. Em uma
região de ionização parcial, o gradiente adiabático
torna-se muito pequeno, e uma zona de convecção se inicia.
Portanto, todas as estrelas que não são quentes o suficiente
para que o hidrogênio esteja completamente ionizado na
fotosfera, têm zonas de convecção próximas à
superfície.

