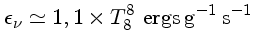Próxima: Áxions
Volta: Interiores Estelares
Anterior: Síntese de Elementos Pesados
Na interação fraca, existe um acoplamento elétron-neutrino
de modo que um par elétron-pósitron pode decair em um
par neutrino-antineutrino pela interação fraca, além
de poder decair em um par de raios
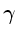 pela interação
eletromagnética. Embora a interação fraca seja cerca de
10-20 mais rara do que a eletromagnética,
no núcleo de
estrelas evoluídas ela pode ser dominante devido à alta densidade.
pela interação
eletromagnética. Embora a interação fraca seja cerca de
10-20 mais rara do que a eletromagnética,
no núcleo de
estrelas evoluídas ela pode ser dominante devido à alta densidade.
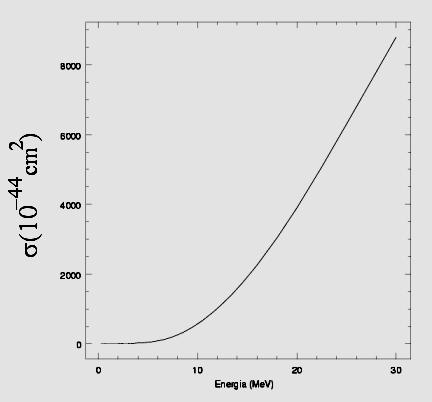
Secção de choque dos neutrinos contra um alvo de gálio, de acordo com
John N. Bahcall (1934-2005), publicado em 1996 no
Physical
Review C, 56, 3391. Existem ressonâncias, como a do neutrino de 15,11 MeV sobre
um alvo de
12C, que leva a uma secção de choque medida de
(9,3 ± 0,6) × 10
-42 cm
2.
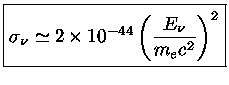
A emissão de neutrinos geralmente funciona como uma refrigeração,
já que os neutrinos interagem muito pouco com a matéria,
devido à sua baixa seção de choque,
e, portanto, escapam do meio carregando energia,
exceto para altíssimas densidades, como durante o colapso
de supernova.
A energia dos neutrinos,
exceto nos casos extremos, não contribui para manter o equilíbrio
hidrostático ou equilíbrio térmico, removendo a energia
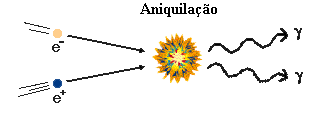
térmica do gás. Os três processos mais importantes
de emissão de neutrinos são: aniquilação de pares
elétron-pósitron formando pares neutrino-antineutrino,
plasma neutrino e processos de fotoneutrinos.
Para temperaturas maiores do que
109 K, necessárias para a queima do C, pares elétron-pósitron
são produzidos nos interiores estelares porque a energia da
radiação é alta o suficiente (kT>0,1 MeV).
Este processo é importante no núcleo de estrelas mais massivas que 8 MSol,
após a queima do He.
Como um fóton tem massa de repouso zero, ele não pode decair
no vácuo em um par elétron-pósitron ou neutrino-antineutrino,
conservando tanto o momentum quanto a energia, já que no centro
de massa do par, tanto a energia quanto o momentum são nulos.
Entretanto, fótons em um gás denso têm uma massa efetiva,
e são chamados de plasmons. A relação de dispersão para
um plasmon transverso de número de onda k em um gás não degenerado,
não relativístico de densidade eletrônica
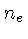 , é dada por
, é dada por
onde a frequência de plasma para um gás não degenerado é dada por
ou seja, a massa efetiva do plasmon é
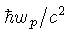 .
Como os plasmons têm massa efetiva, eles podem decair em
pares. Este processo é chamado de plasma neutrinos, e
é dominante na remoção de energia térmica de
núcleos degenerados de gigantes vermelhas, núcleos
de nebulosas planetárias e anãs brancas quentes.
.
Como os plasmons têm massa efetiva, eles podem decair em
pares. Este processo é chamado de plasma neutrinos, e
é dominante na remoção de energia térmica de
núcleos degenerados de gigantes vermelhas, núcleos
de nebulosas planetárias e anãs brancas quentes.
Se o gás de elétrons for degenerado, a freqüência de plasma é dada por:
O processo chamado de fotoneutrino dá-se quando um
fóton energético interage com um elétron,
produzindo um par neutrino-antineutrino:
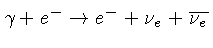
Este processo é importante no núcleo degenerado de estrelas quentes.
 Mário Schenberg
Mário Schenberg (1916-1990),
pernambucano, formou-se em Engenharia e Matemática na USP em 1936, trabalhou na Europa com Enrico
Fermi e Wolfgang Pauli na teoria de neutrinos em 1938 e 1939 e, quando
em 1940 foi trabalhar em Washington com George Gamow, viu que ele não estava incluindo
a perda de energia por neutrinos nos cálculos de colapso de supernova.
Depois em 1941, foi para Princeton trabalhar com Subramanian Chandrasekhar (1910-1995),
retornando ao Brasil em 1942. Foi eleito para a Assembléia Constituinte
em 1945, pelo Partido Comunista Brasileiro, mas foi cassado em seguida.
Preso por subversão no ano seguinte, quando liberado alguns meses
depois foi para Bruxelas, onde trabalhou 5 anos. Returnou ao Brasil
em 1953 e foi diretor do Instituto de Física da USP até 1961.
Em 1962 foi eleito deputado estadual pelo PTB e foi impedido de
assumir "por ser comunista". Foi preso em 1964, e retornou à USP em 1965,
mais em 1968 foi atingido pelo Ato Institucional número 5,
aposentado compulsoriamente e impedido de frequentar a universidade.
Em 1979, com a Anistia, voltou para a USP.
O processo Urca de emissão de neutrinos,
em honra ao Casino
da Urca, no Rio, em que se perdia de qualquer forma,
foi proposto pelo físico russo-americano
George Antonovich Gamow (1904-1968)
e pelo físico brasileiro
Mário Schenberg
(Gamow & Schoenberg.
1941, Physical Review. 59, 539).
Ele consiste de uma captura de elétron
por um elemento químico qualquer (Z,A):
seguida de um decaimento 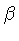 :
O neutrino e antineutrino são formados sem qualquer alteração
da composição química, retirando energia do meio.
:
O neutrino e antineutrino são formados sem qualquer alteração
da composição química, retirando energia do meio.

 O cálculo da taxa de produção de neutrinos é baseado na
teoria eletrofraca de Steven Weinberg (1933-2021), publicada no
"A Model of Leptons ", Physics Review Letter, 19, 1264 em 1967, e Abdus Salam (1926-1996),
1963, "Renormalizable Electrodynamics of Vector Mesons", Physical Review,
130, 1287.
O cálculo da taxa de produção de neutrinos é baseado na
teoria eletrofraca de Steven Weinberg (1933-2021), publicada no
"A Model of Leptons ", Physics Review Letter, 19, 1264 em 1967, e Abdus Salam (1926-1996),
1963, "Renormalizable Electrodynamics of Vector Mesons", Physical Review,
130, 1287.
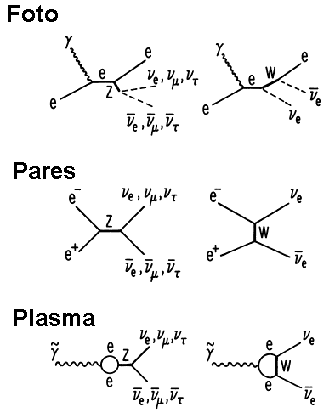 Diagramas de Feyman para os mecanismos
de emissão de neutrinos.
Na esquerda são apresentados os diagramas envolvendo correntes neutras e
na direita os com correntes carregadas. Somente neutrinos e antineutrinos
de elétrons são formados através de interações com correntes carregadas.
Diagramas de Feyman para os mecanismos
de emissão de neutrinos.
Na esquerda são apresentados os diagramas envolvendo correntes neutras e
na direita os com correntes carregadas. Somente neutrinos e antineutrinos
de elétrons são formados através de interações com correntes carregadas.
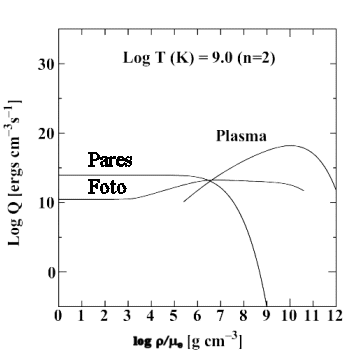
- Q ~ 102 ergs cm-3 s-1,
para T = 107 K e log g = 6,
equivalente ao núcleo de uma estrela anã branca próxima
de Tef~
13 000 K,
para
- Q ~ 1015 ergs cm-3 s-1,
para T = 109 K e log g = 9,
equivalente ao núcleo de uma estrela anã branca quente,
chegando a
- Q ~ 1018 ergs cm-3 s-1,
para T = 109 K e log g = 14, para uma estrela de nêutrons.
Alguns valores aproximados para as taxas de produção de neutrinos são:
para 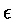 e
e 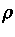 em cgs.
onde
para
em cgs.
onde
para 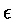 e
e 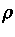 em cgs.
para
em cgs.
para 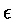 e
e 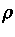 em cgs, e onde
e
em cgs, e onde
e 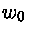 é a freqüência de plasma:
é a freqüência de plasma:
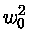 |
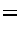 |
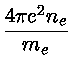 não-degenerado não-degenerado |
|
| |
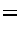 |
![$ \frac{4\pi e^2 n_e}{m_e}[1+(\frac{\hbar}{m_ec})^2
(3\pi^2 n_e)^{-\frac{2}{3}}]^{-\frac{1}{2}}$](neut/img23.gif) degenerado degenerado |
|
para 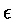 e
e 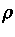 em cgs.
em cgs.
Em um gás não degenerado, a remoção de energia térmica
causa contração do núcleo. Pelo teorema de Virial,
quando a densidade aumenta, a temperatura também aumenta.
Entretanto, em um gás degenerado, a pressão é praticamente
independente da temperatura, e uma redução da energia
térmica causa redução da temperatura. No núcleo
degenerado de estrelas de massa até cerca de 10 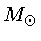 ,
o esfriamento pelo processo de plasma neutrinos, e em menor
grau pelo processo de emissão de fotoneutrinos, inibe
a elevação da temperatura no núcleo para as temperaturas
necessárias para o início da queima do carbono.
Se a massa total for suficiente para
que a massa do núcleo atinja o limite da massa máxima de
uma anã branca, com densidades nucleares da ordem de
1 a
,
o esfriamento pelo processo de plasma neutrinos, e em menor
grau pelo processo de emissão de fotoneutrinos, inibe
a elevação da temperatura no núcleo para as temperaturas
necessárias para o início da queima do carbono.
Se a massa total for suficiente para
que a massa do núcleo atinja o limite da massa máxima de
uma anã branca, com densidades nucleares da ordem de
1 a
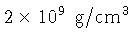 , inicia-se a queima
explosiva do carbono em um núcleo altamente degenerado,
resultando em uma supernova.
, inicia-se a queima
explosiva do carbono em um núcleo altamente degenerado,
resultando em uma supernova.
 Taxas de emissão de neutrinos foram
calculadas pelo astrofísico japonês Naoki Itoh, publicadas
em 1996 no
Astrophysical Journal, 102, 411-424, e
estão disponíveis na forma de tabelas ou de subrotinas
FORTRAN em
http://nile.ph.sophia.ac.jp/~itoh-ken/subroutine/subroutine.htm. Na mesma página
estão referências para os cálculos recentes de condução
eletrônica e escudamento eletrônico (electron screening).
Taxas de emissão de neutrinos foram
calculadas pelo astrofísico japonês Naoki Itoh, publicadas
em 1996 no
Astrophysical Journal, 102, 411-424, e
estão disponíveis na forma de tabelas ou de subrotinas
FORTRAN em
http://nile.ph.sophia.ac.jp/~itoh-ken/subroutine/subroutine.htm. Na mesma página
estão referências para os cálculos recentes de condução
eletrônica e escudamento eletrônico (electron screening).
Programas
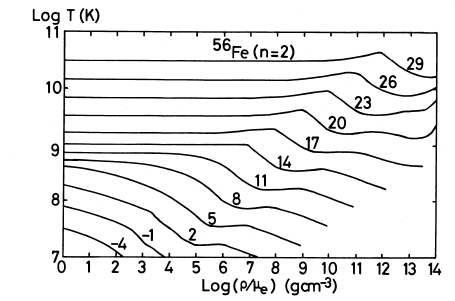
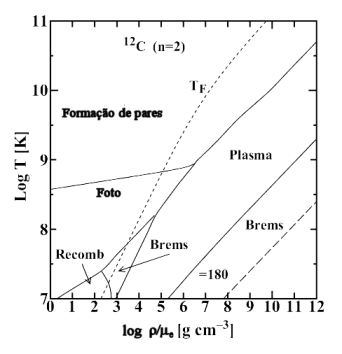
Contornos para a taxa de perda de energia por unidade de volume e por
unidade de tempo pela emissão de neutrinos, em unidades de log Q
(ergs cm
-3 s
-1), somando-se todas as perdas de neutrinos
por produção de pares, foto-neutrinos, plasma-neutrinos e bremsstrahlung.
Para
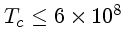 K e densidades
K e densidades
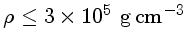 ,
de modo que a luminosidade de neutrinos é, em geral, maior do
que a luminosidade dos fótons, para
,
de modo que a luminosidade de neutrinos é, em geral, maior do
que a luminosidade dos fótons, para
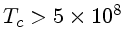 K.
K.
Elena M. Kantor e Mikhail E. Gusakov,
do grupo de estrelas de nêutrons do IOFFE, publicaram
em 2007 novos cálculos para a emissividade de neutrinos, sem algumas aproximações
na função dielétrica e nas relações de dispersão dos plasmons feitas por Itoh, que divergiam para altas
densidades em temperaturas intermediárias.
A tabela está disponível em
http://www.ioffe.ru/astro/NSG/plasmon/table.dat.
As estrelas anãs brancas têm uma primeira fase em que o esfriamento por neutrinos devido ao decaimento
de plasmons é dominante, antes de entrar em uma fase em que o esfriamento por fótons é dominante.
Juan Carlos D'Olivo e José F. Nieves calcularam em 1998
(Physical Review D, 57, 3116)
os efeitos do meio (nucleons)
sobre as relações de dispersão dos fótons, incluindo os efeitos de auto-energia e
momentum magnético anômalo, incluindo os efeitos relativísticos e de
degenerescência, e em 2003 (Physical Review D, 67, 5018)
Juan Carlos D'Olivo, José F. Nieves e
Sarira Sahu incluiram o efeito da rotação de Faraday.
Wick C. Haxton (1949-), Robert Graham Hamish Robertson (1943-) e Aldo M. Serenelli (2012) astroph.1208.5723 fazem uma revisão das
observações e suas implicações até 2012, incluindo as medidas do Borexino
dos neutrinos das cadeias ppI e ppII.
No artigo
Recent developments for realistic solar models,
AIP Conf. Proc. 1594, 137 (2014)
Aldo Serenelli relata as dificuldades atuais,
principalmente a quase total inexistência de dados experimentais para as opacidades radiativas e a grande dificuldade em medir-se as abundâncias
químicas e, além disto, calcular as abundâncias primordiais.





Próxima: Neutrinos Massivos
Volta: Interiores Estelares
Anterior: Síntese de Elementos Pesados
©
Modificada em 15 set 2014

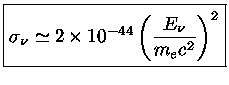
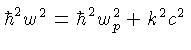
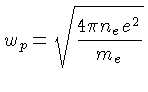
![w_p^2 = \frac{4\pi n_e e^2}{m_e}[1+(\frac{\hbar}{m_e c})^2
(3\pi^2 n_e)^{2/3}]^{-\frac{1}{2}}$](wpd.gif)


 O cálculo da taxa de produção de neutrinos é baseado na
teoria eletrofraca de Steven Weinberg (1933-2021), publicada no
"A Model of Leptons ", Physics Review Letter, 19, 1264 em 1967, e Abdus Salam (1926-1996),
1963, "Renormalizable Electrodynamics of Vector Mesons", Physical Review,
130, 1287.
O cálculo da taxa de produção de neutrinos é baseado na
teoria eletrofraca de Steven Weinberg (1933-2021), publicada no
"A Model of Leptons ", Physics Review Letter, 19, 1264 em 1967, e Abdus Salam (1926-1996),
1963, "Renormalizable Electrodynamics of Vector Mesons", Physical Review,
130, 1287.

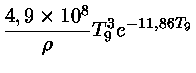
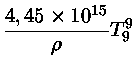
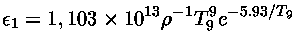
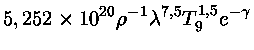
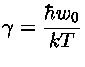
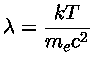
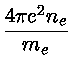 não-degenerado
não-degenerado![$ \frac{4\pi e^2 n_e}{m_e}[1+(\frac{\hbar}{m_ec})^2
(3\pi^2 n_e)^{-\frac{2}{3}}]^{-\frac{1}{2}}$](neut/img23.gif) degenerado
degenerado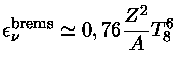
 Taxas de emissão de neutrinos foram
calculadas pelo astrofísico japonês Naoki Itoh, publicadas
em 1996 no
Taxas de emissão de neutrinos foram
calculadas pelo astrofísico japonês Naoki Itoh, publicadas
em 1996 no