

Em 1956 Chien-Shiung Wu (1912-1997) demonstrou que o decaimento do Co60 ocorria mais antiparalelo ao spin do núcleo, violando a simetria de paridade (espelhamento). Em 1957 Lev Davidovich Landau (1908-1968) propos que a boa simetria era CP, ou carga e paridade, isto é, trocando-se a partícula pela antipartícula e trocando a paridade simultaneamente. Mas em 1964 o decaimento do kaon demonstrou que a CP é também violada pela força fraca, por James Watson Cronin (1931-2016) e Val Logsdon Fitch (1923-2015), no Physical Review Letters, 13, 138. Esta observação da violação da carga-paridade lhes deu o prêmio Nobel de 1980, e é fundamental para explicar por que existe mais matéria do que antimatéria no Universo, como proposto por Andrei Dmitrievich Sakharov (1921-1089) em 1967 (Prêmio Nobel da Paz em 1975).
A existência do áxion, um bóson hipotético de spin zero, foi postulada em 1977 pelo italiano Roberto Daniele Peccei (1942-2020) e pela australiana Helen Rhoda Arnold Quinn (1943-) (Physical Review Letters, 38, 1440) para explicar porque as interações fortes e eletromagnéticas conservam paridade (P) e carga/paridade (CP), apesar das interações fracas violarem estas simetrias. A falta de violação de P e CP nas interações fortes é conhecida como "o grande problema de CP", pois requer um parâmetro de interação na força forte extremamente pequeno (<10-9), mas não nulo. O áxion resolve este problema, e é um candidato a matéria escura [Jihn E. Kim, 2014, arXiv 1409.3609v1]. Embora nunca tenham sido diretamente observados, sua teoria prediz que os áxions são criados quando fótons interagem com campos magnéticos ou cargas elétricas, o que acontece no centro das estrelas, de modo que observações astrofísicas podem colocar limites nas taxas de produção de áxions. Existem também outras propostas de solução do problema de CP, como impor que a massa de um quark seja nula, mu = 0, ou assumir que as simetrias P e CP são quebradas espontaneamente, mas são boas simetrias. Uma simetria global ou rígida é a mesma em todo o espaço-tempo e geralmente leva a uma quantidade conservada.
Permitir que as transformações da simetria variem continuamente de um local no espaço-tempo para outro requer a introdução de novos
graus de liberdade "gauge" mediando as forças.
Uma teoria com simetria de gauge
pode ser escrita em termos
de potenciais em que somente diferenças de
potenciais
são significativas, isto é, podemos adicionar uma
constante sem alterar os valores. Por exemplo, um esquilo
pode caminhar sobre um fio de alta tensão porque somente
diferenças de potenciais são importantes. Estas
teorias portanto podem ser renormalizadas.
 É este princípio de transformações
de gauge que permitiu a construção do modelo padrão
da força forte e eletrofraca entre as partículas elementares
baseados no grupo local gauge
É este princípio de transformações
de gauge que permitiu a construção do modelo padrão
da força forte e eletrofraca entre as partículas elementares
baseados no grupo local gauge
![]() .
.
A quebra de uma simetria global leva a um bóson de Goldstone, sem massa, escalar. Na
quebra de simetrias locais (gauge),
o bóson de Goldstone [Jeffrey Goldstone (1933-)]
conspira com o campo gauge, sem massa,
formando um campo vetorial massivo, no fenômeno conhecido como
mecanismo de Higgs [Peter Ware Higgs (1929-)].
Um exemplo é a quebra de simetria da força eletrofraca,
que no modelo de Glashow-Weinberg-Salam onde o grupo gauge
![]() se quebra no grupo U(1) do eletromagnetismo. Neste contexto,
as partículas vetoriais massivas correspondem aos bósons W e Z
que mediam a força fraca, de curta distância. Na quebra de simetria,
todas as partículas exceto o fótons adquirem um estado de
polarização
adicional e tornam-se massivos.
se quebra no grupo U(1) do eletromagnetismo. Neste contexto,
as partículas vetoriais massivas correspondem aos bósons W e Z
que mediam a força fraca, de curta distância. Na quebra de simetria,
todas as partículas exceto o fótons adquirem um estado de
polarização
adicional e tornam-se massivos.
Uma aplicação especulativa do mecanismo de Higgs é a da Teoria de Grande Unificação (GUT), unificando a força forte com a eletrofraca, com um grande grupo gauge SU5.
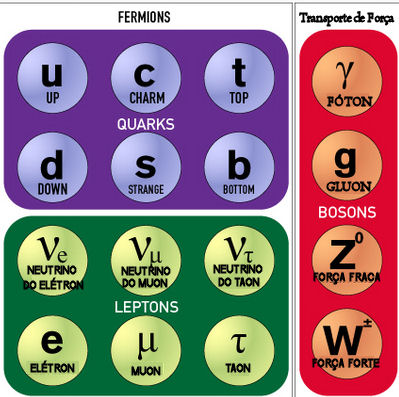
Na teoria padrão de campos, existem seis léptons e seis quarks.
Esta teoria é não-abeliana, isto é, as transformações
dependem da ordem.
Os mediadores da força eletro-fraca são o fóton, sem massa,
e as três partículas de campo (bósons)
![]() ,
, ![]() e
e
![]() . A força
forte é carregada pelos oito glúons, todos sem massa, e a teoria
prediz a existência do bóson de Higgs
. A força
forte é carregada pelos oito glúons, todos sem massa, e a teoria
prediz a existência do bóson de Higgs ![]() , cujo campo gera
a massa de todas as outras partículas. A procura direta do bósons de
Higgs
levou à detecção nos experimentos Atlas e CMS do
Large Hadron Collider no CERN em 2012.
O valor atual dos dois experimentos
é mH=125,36±0,37 (incerteza estatística) ±0,18 (incerteza sistemática) GeV/c2
[Georges Aad e a colaboração ATLAS,
Physical Review D 90, 052004 (2014)].
François Englert (1932-) e Peter Higgs receberam o prêmio Nobel de 2013.
, cujo campo gera
a massa de todas as outras partículas. A procura direta do bósons de
Higgs
levou à detecção nos experimentos Atlas e CMS do
Large Hadron Collider no CERN em 2012.
O valor atual dos dois experimentos
é mH=125,36±0,37 (incerteza estatística) ±0,18 (incerteza sistemática) GeV/c2
[Georges Aad e a colaboração ATLAS,
Physical Review D 90, 052004 (2014)].
François Englert (1932-) e Peter Higgs receberam o prêmio Nobel de 2013.
Por simetria com o decaimento do nêutron, o próton deve decair em:
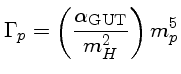
Os áxions são
pseudo bósons de
Yoishiro Nambu (1921-2015) e Jeffrey Goldstone (1933-), com
spin zero,

 propostos por Roberto D. Peccei (1942-) e Helen R. Quinn (1943-),
de Stanford, em 1977, no Physical Review Letters, vol. 38, no. 25, 1440,
para explicar a simetria que suprime a grande violação CP
(carga-paridade) na QCD (cromodinâmica quântica).
propostos por Roberto D. Peccei (1942-) e Helen R. Quinn (1943-),
de Stanford, em 1977, no Physical Review Letters, vol. 38, no. 25, 1440,
para explicar a simetria que suprime a grande violação CP
(carga-paridade) na QCD (cromodinâmica quântica).
Os áxions têm acoplamentos extremamente fracos com a matéria e
radiação, e massa, no modelo DFSZ, dada por:
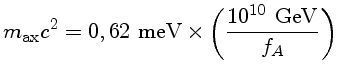
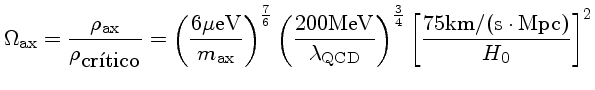
No modelo de Kim, a massa do áxion é proporcional à massa do quark pesado Q:
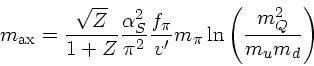
No modelo DFSZ a massa é
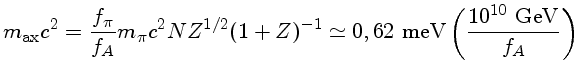
A massa
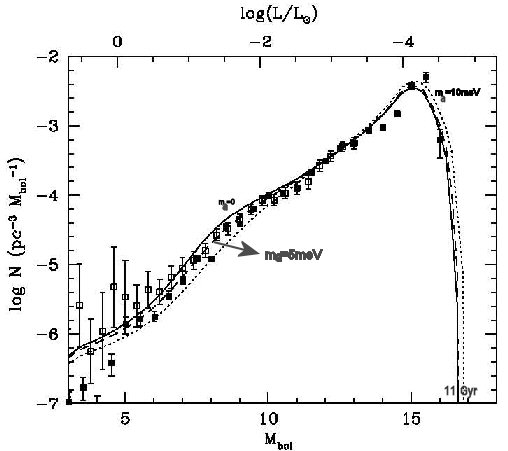
do áxions precisa ser menor do que 10 meV/c2 ou sua produção
numerosa no ramo das estrelas gigantes causaria uma enorme
refrigeração no núcleo destas estrelas, não observado.
Uma massa menor que
10 meV/c2 leva a um valor esperado da energia do vácuo maior que ![]() GeV.
Como o modo principal de decaimento do áxion a é
GeV.
Como o modo principal de decaimento do áxion a é
![]() ,
os áxions podem ser detectados estimulando-se sua conversão
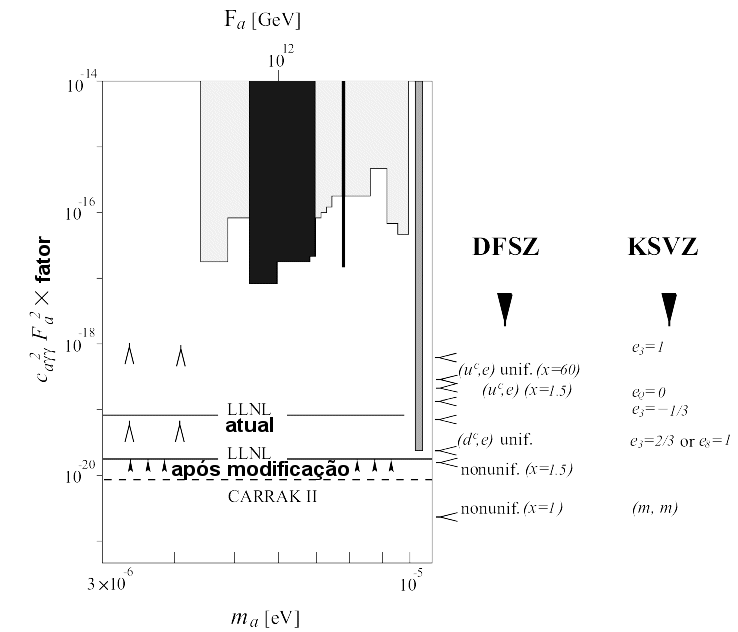
em fótons em um forte campo magnético. Experimentos no
Lawrence Livermore National Laboratory
e na Universidade da Flórida estão testando massas
,
os áxions podem ser detectados estimulando-se sua conversão
em fótons em um forte campo magnético. Experimentos no
Lawrence Livermore National Laboratory
e na Universidade da Flórida estão testando massas
![]() eV/c2
(Christian A. Hagmann, S. Chang e Pierre Sikivie, 2001, Physical Review D, 63, 125018).
Na Kyoto University estão buscando o áxion próximo de
eV/c2
(Christian A. Hagmann, S. Chang e Pierre Sikivie, 2001, Physical Review D, 63, 125018).
Na Kyoto University estão buscando o áxion próximo de
![]() eV/c2
(Ikuyo Ogawa, S. Matsuki e K. Yamamoto, 1996, Physical Review D, 53, 1740).
eV/c2
(Ikuyo Ogawa, S. Matsuki e K. Yamamoto, 1996, Physical Review D, 53, 1740).
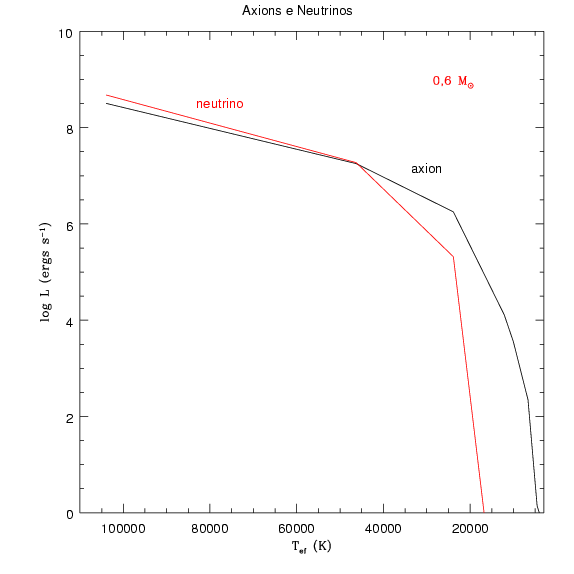
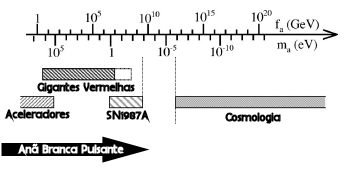
Em 1992, Jordi Isern, Margareta Hernanz e Enrique García-Berro publicaram
um artigo no Astrophysical Journal, 392, L23,
usando o valor de dP/dt da anã branca G117-B15A,
publicado por S.O. Kepler et al. em 1991 no Astrophysical Journal, 378, L45,
para limitar a massa dos áxions para
![]() meV/c2.
O valor de dP/dt publicado em 1991, maior do que o esperado,
poderia ser devido ao esfriamento por áxions.
meV/c2.
O valor de dP/dt publicado em 1991, maior do que o esperado,
poderia ser devido ao esfriamento por áxions.
No artigo "The potential of the variable DA white dwarf G117-B15A as a tool for Fundamental Physics" de Alejandro H. Córsico, Omar G. Benvenuto, Leandro G. Althaus, Jordi Isern e Enrique García-Berro, publicado em 2001 no New Astronomy, vol. 6, no. 4, 197, Córsico e colaboradores da Universidad Nacional de La Plata, na Argentina, e da Espanha, calculam um modelo de anã-branca com os três períodos principais de G117-B15A e, usando a taxa de produção de energia por áxions no modelo DFSZ predita por Masayuki Nakagawa, Tomoo Adashi, Yasuharu Kohyama e Naoki Itoh, da Sophia University, Tokyo, publicadas em 1988 no Astrophysical Journal, 326, 241,
Com a determinação da taxa de variação do período de pulsação do relógio ótico mais estável conhecido por S. O. Kepler, D. E. Winget, Zachary P. Vanderbosch, Barbara Garcia Castanheira, J. J. Hermes, Keaton J. Bell, Fergal Mullally, Alejandra D. Romero, M. H. Montgomery, Steven DeGennaro, Karen I. Winget, Dean Chandler, Elizabeth J. Jeffery, Jamile K. Fritzen, Kurtis A. Williams, Paul Chote, & Staszek Zola em 2021, no artigo The Pulsating White Dwarf G117-B15A: Still the Most Stable Optical Clock Known, The Astrophysical Journal, 906, 7, a detecção do áxion ficou em maxion=19.9±3.1 meV.
![L = 1,08 \times 10^{23} \rho~ergs g_{ae}^{-1} s^{-1} T^4[F_{fonons}+F_{rede}+F_{liquido}]](img2.gif)
No Microwave cavity searches for dark-matter axions
(Reviews of Modern Physics. 2003, vol. 75, 3, p. 777),
Richard Bradley, John Clarke, Darin Kinion, Leslie J. Rosenberg,
Karl van Bibber, Seishi Matsuki, Michael Mück &
Pierre Sikivie discutem como o áxion é um bom candidato para
a matéria escura do Universo e como se pode, em princícipio,
detectá-los em uma cavidade de microondas permeada por
um campo magnético intenso, onde eles se convertem em fótons
quasi-monocromáticos
pela interação de Primakoff
[Henry Primakoff (1914-1983) 1937, Physical Review, 51, 990],
isto é,
interação com o campo eletromagnético
![]() .
Devido à sua baixa interação, mesmo com
1014 axions/cm3
se sua massa fosse 10
.
Devido à sua baixa interação, mesmo com
1014 axions/cm3
se sua massa fosse 10 ![]() eV/c2, eles produziriam somente 10-23W,
de modo que sua detecção requer detectores com ruído
muito próximo do ruído quântico.
eV/c2, eles produziriam somente 10-23W,
de modo que sua detecção requer detectores com ruído
muito próximo do ruído quântico.
A não detecção pelo CERN Axion Solar Telescope limita a massa a 0,02 eV/c2 (K. Zioutas et al. 2005, Physical Review Letters, 94, 121301), correspondente a um acoplamento áxion-fóton gaf<1.16×10-10 GeV-1.
A relação entre a constante de acoplamento e o valor esperado do vácuo no momento da quebra de simetria é
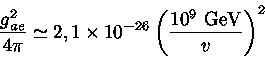
Córsico e colaboradores estimam o
limite máximo de
esfriamento por áxions consistente com as medidas de Kepler Oliveira
[S.O. Kepler,
José Eduardo da Silveira Costa, Bárbara Garcia Castanheira,
Donald Earl Winget,
Fergal Mullally,
R. Edward Nather,
Mukremin Kilic, Ted von Hippel,
Anjum S. Mukadam &
Denis J. Sullivan.
"Measuring the Evolution of the Most Stable Optical Clock G 117-B15A",
2005,
Astrophysical Journal,
634, 1311-1318]
e limitam a massa massa dos áxions
a
![]() meV/c2, com 95% de confiança.
meV/c2, com 95% de confiança.
Matéria e antimatéria: uma relação não muito simétrica,mostra que a assimetria, normalmente de 10%, pode chegar a 80% em alguns experimentos envolvendo o decaimento de mésons B em três partículas.
Experimento de matéria escura e Explicação com ficção (pdf)