




Próxima: Polítropos
Volta: Interiores Estelares
Anterior: Síntese de Elementos Pesados
Com as quatro equações diferenciais:
-
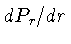 equação de equilíbrio hidrostático,
equação de equilíbrio hidrostático,
-
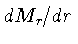 continuidade de massa,
continuidade de massa,
-
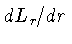 conservação de energia
conservação de energia
e
-
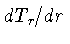 transporte de energia,
se radiativo, ou, se convectivo,
transporte de energia,
se radiativo, ou, se convectivo,
- a equação de estado do gás,
- a opacidade e
- a equação de geração de energia,
além das condições de contorno:
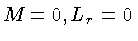
em r=0
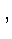
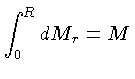
em r=R
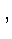
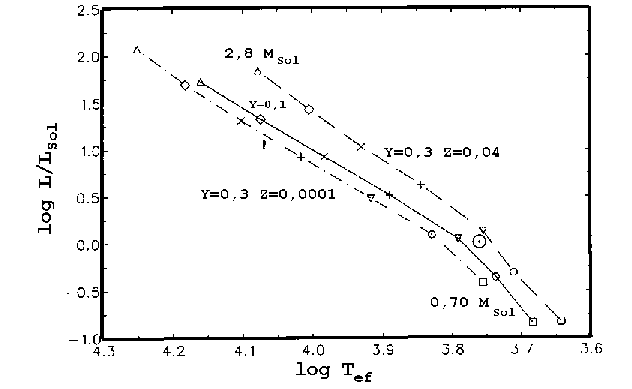
e dados a massa total (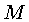 ) e a composição química,
calculamos primeiro o modelo em equilíbrio com
composição homogênea, que define a sequência principal
de idade zero, e sucessivos estados de equilíbrio.
Para funções realísticas, não é possível
obter-se soluções analíticas, de modo que o
sistema de equações diferenciais acopladas precisa
ser resolvido numericamente.
) e a composição química,
calculamos primeiro o modelo em equilíbrio com
composição homogênea, que define a sequência principal
de idade zero, e sucessivos estados de equilíbrio.
Para funções realísticas, não é possível
obter-se soluções analíticas, de modo que o
sistema de equações diferenciais acopladas precisa
ser resolvido numericamente.
Em 1926 Heinrich Vogt (1890-1968), em seu artigo
"A Relação entre a Massa e a Luminosidade das Estrelas"
["Die Beziehung zwischen den Massen und den absoluten Leuchtkräften der Sterne",
Astronomische Nachrichten 226, 301]
e Henry Norris Russel (1877-1957)
[Henry Norris Russell, Raymond Smith Dugan
(1878-1940) e John Quincy Stewart (1894-1972), Astronomy II,
1927, p. 909-911]
propuseram o chamado teorema de Vogt-Russel,
sem qualquer base matemática, que afirma que
para dada massa total e composição química,
existe uma e somente uma solução para
as equações básicas de estrutura estelar.
Numericamente, quando uma sequência evolucionária
chega a um ponto onde nenhuma solução em equilíbrio
pode ser encontrada, alguma aproximação utilizada
não é mais válida, e precisamos relaxar
as condições, por exemplo de equilíbrio térmico.
Alfred Gautschy
discute como este não é um teorema.
Programas
Modelos de Sequência Principal de Idade Zero
q
c é a fração do núcleo convectivo
e q
e é o envelope convectivo.
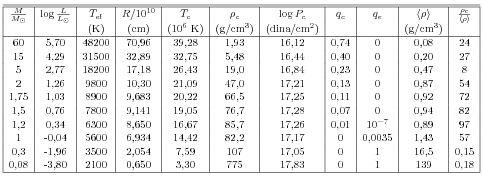
Sequência Principal de Idade Zero para modelos
com diferentes composições químicas. A sequência
com Y=0,1 tem Z=0,0001.
Nos modelos com MLT, existem entretanto
três parâmetros ajustáveis: comprimento
de mistura, eficiência de perda de massa e quantidade de
sobreimpulso
(overshooting) de convecção, além da
variação da composição química do
modelo, que afetam os resultados. Os modelos mostram que,
para temperaturas efetivas menores do que 7000 K,
o hidrogênio estará neutro na atmosfera da estrela e,
portanto, há uma zona de ionização parcial do hidrogênio
em uma camada mais profunda. Nesta zona de ionização parcial,
a opacidade é alta e dificulta o transporte radiativo de energia.
Desenvolve-se portanto uma camada de convecção superficial.
Para as estrelas mais quentes, não há zona de ionização parcial
e, portanto, não há convecção superficial. As
estrelas de baixa massa, como nosso Sol, transformam hidrogênio
em hélio pelo ciclo próton-próton (pp), enquanto
que as estrelas massivas transformam pelo ciclo CNO. O limite
se dá para estrelas de cerca de 1,25 a 1,75 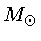 , dependendo da metalicidade, para
as quais
, dependendo da metalicidade, para
as quais
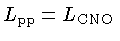 . Para as
estrelas com queima de hidrogênio pelo ciclo CNO,
a taxa de geração de energia varia com uma alta potência
da temperatura
(
. Para as
estrelas com queima de hidrogênio pelo ciclo CNO,
a taxa de geração de energia varia com uma alta potência
da temperatura
(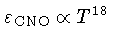 ),
gerando um forte gradiente de temperatura na
borda superior do núcleo, o que causa uma zona de convecção
no núcleo.
),
gerando um forte gradiente de temperatura na
borda superior do núcleo, o que causa uma zona de convecção
no núcleo.
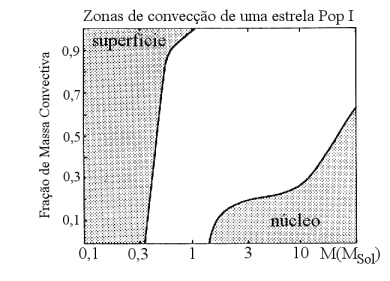 Regiões de convecção para estrelas de população 1. Abaixo de 0,3
MSol as estrelas são completamente convectivas.
Regiões de convecção para estrelas de população 1. Abaixo de 0,3
MSol as estrelas são completamente convectivas.
Outros limites importantes são que para
massa menor do que 2,25 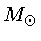 (ou 1,85
(ou 1,85 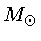 se o overshooting for importante),
o início da transformação
de hélio em carbono se dá em um núcleo com elétrons degenerados,
causando um flash de hélio, isto é, um forte aumento de luminosidade,
antes que o núcleo possa se reajustar em uma queima quiescente.
se o overshooting for importante),
o início da transformação
de hélio em carbono se dá em um núcleo com elétrons degenerados,
causando um flash de hélio, isto é, um forte aumento de luminosidade,
antes que o núcleo possa se reajustar em uma queima quiescente.
Antonio Claret, no Astronomy and Astrophysics, (2007) 475, 1019,
e
Claud H. Sandberg Lacy, Guillermo Torres e Antonio Claret,
no Astronomical Journal, (2008) 135, 1757,
encontram
que um overshooting moderado, αov=0,2,
fita melhor as dimensões absolutas de
binárias eclipsantes bem medidas.
Michael Gruberbauer, David B. Guenther e Thomas Kallinger, em seu artigo de 2012 arXiv:1202.2330, fazem uma análise estatística da heliosismologia e
obtém uma idade para o Sol de (4,591±0,005) bilhões de anos, incluindo uma fase
pré-sequência princial de (35±5) milhões de anos,
e uma composição inicial de X0= 0,72, Y0= 0,264, Z0= 0,016, αML=2,1±0,2.
Dados e Programas





Próxima: Polítropos
Volta: Interiores Estelares
Anterior: Emissão de Neutrinos
©
Modificada em 1 maio 2015
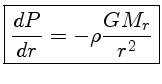
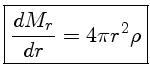
![${\frac{dL_r}{dr}=4\pi r^2\rho[\varepsilon-\frac{3}{2}\rho^{\frac{2}{3}}\frac{d}{dt}(\frac{P}{\rho^{\frac{5}{3}}})]}$](img12.png)
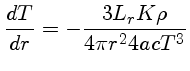
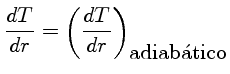
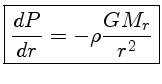
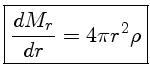
![${\frac{dL_r}{dr}=4\pi r^2\rho[\varepsilon-\frac{3}{2}\rho^{\frac{2}{3}}\frac{d}{dt}(\frac{P}{\rho^{\frac{5}{3}}})]}$](img12.png)
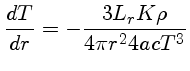
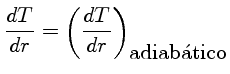
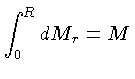 em r=R
em r=R

