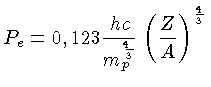 |
(1.78) |
O limite de massa de Chandrasekhar
![]() é a massa máxima que uma anã branca pode ter e ainda
ser suportada pela pressão de degenerescência dos elétrons;
é a massa máxima que uma anã branca pode ter e ainda
ser suportada pela pressão de degenerescência dos elétrons;
![]() é o peso molecular médio
(
é o peso molecular médio
(![]() para hélio, carbono ou oxigênio).
para hélio, carbono ou oxigênio).
Tetsuo Hamada & Edwin Ernest Salpeter (1924-2008) publicaram em 1961 no Astrophysical Journal, 134, 683, correções devido às interações eletrostáticas entre os íons, os desvios de Thomas-Fermi da distribuição não uniforme das cargas dos elétrons e a energia de troca das interações spin-spin. Demonstraram que em altas densidades os decaimentos β inversos tornam-se importantes, e os elétrons tunelam para dentro dos núcleos, formando nêutrons, e mudando efetivamente o peso molecular médio dos elétrons. Quando a densidade do núcleo atinge um certo valor crítico, os elétrons começam a ser pressionados para dentro dos prótons, o que também define um processo de decaimento β inverso, criando nêutrons e neutrinos. A estrutura nuclear dentro do núcleo da anã branca muda. Quando as transições de fase se iniciam, uma parte do núcleo estelar é composto de núcleos pesados, mudando efetivamente o índice adiabático da estrela. Entretanto, ultrapassar esta densidade crítica, que leva às transições de fase, não é suficiente para causar a instabilidade, que requer ou uma grande diferença entre a densidade do núcleo da estrela e as camadas externas (William H. Ramsey, 1950, Monthly Notices of the Royal Astronomical Society, 110, 444 15),
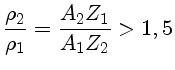
Outra componente que tem efeito sobre a massa máxima de uma anã branca é a Relatividade Geral. Inicialmente proposto por Samuil Aronovich Kaplan (1921-1978) em 1949 (Zhurnal Eksperimental noi i Teoreticheskoi Fiziki, 19, 951 16) e calculado precisamente em 1964 por Subrahmanyan Chandrasekhar (1910-1995) e Robert F. Tooper, no Astrophysical Journal, 139, 1396 e Subrahmanyan Chandrasekhar no Astrophysical Journal, 140, 417 (e errata), e precisamos utilizar a equação de equilíbrio hidrostático da relatividade geral. Este efeito quebra a estabilidade dinâmica a densidades mais baixas que aquelas calculadas para os modelos de temperatura zero, reduzindo a massa de Chandrasekhar para 98% da massa de Chandrasekhar sem correção relativística
Note que como raio das anãs brancas, Rab≅ 10 000 km, é mais de mil vezes o raio de Schwarzschild de mesma massa, RSch≅3 km, os efeitos relativísticos são muito pequenos. O mesmo raciocínio mostra que para estrelas de nêutrons, com raios da ordem de 10 km, os efeitos relativísticos são importantes.O artigo Relativistic Feynman-Metropolis-Teller theory for white dwarfs in general relativity, de Michael Rotondo, Jorge A. Rueda, Remo Ruffini & She-Sheng Xue, publicado em 2011 no Physical Review D, 84, h4007, leva em conta a relatividade geral, o decaimento beta inverso (neutron drip) e o escudamento eletrônico dentro das células de Wigner-Seitz, para calcular a massa máxima para composições químicas diferentes, obtendo valores um pouco menores do que Hamada & Salpeter, 1,409 MSol para He, 1,386 MSol para C, 1,380 MSol para O, 1,106 MSol para Fe.
No artigo General Relativistic Calculations for White Dwarf Stars, de Arun Mathew e Malay K. Nandy, no arXiv:1401.0819v3, eles calculam que a massa máxima para núcleos de C é 1,3916 MSol, 1,3846 MSol para O816, 1,3702 para Ne1020 e Fe é 1,157 MSol, comparando a massa de neutronização com a massa de estabilidade, mas sem levar em conta a neutralidade na célula de Wigner-Seitz.
Várias anãs brancas são encontradas com massas abaixo de
0,50 ![]() ; os modelos de evolução estelar
indicam que estas estrelas não passaram pela fase luminosa (topo)
do ramo gigante assintótico (AGB), fase de Mira e subseqüente
fase de nebulosa planetária, mas sim tiveram perda de
massa suficientemente alta para truncar sua evolução
no início do AGB, ou ainda no ramo horizontal,
onde há queima de hélio no núcleo. Uma razão para
esta truncagem seria se a camada rica em hidrogênio próxima
à superfície não tiver massa suficiente para manter ignição
e reignição de queima de hidrogênio (shell flashes).
; os modelos de evolução estelar
indicam que estas estrelas não passaram pela fase luminosa (topo)
do ramo gigante assintótico (AGB), fase de Mira e subseqüente
fase de nebulosa planetária, mas sim tiveram perda de
massa suficientemente alta para truncar sua evolução
no início do AGB, ou ainda no ramo horizontal,
onde há queima de hélio no núcleo. Uma razão para
esta truncagem seria se a camada rica em hidrogênio próxima
à superfície não tiver massa suficiente para manter ignição
e reignição de queima de hidrogênio (shell flashes).
A composição química do núcleo das anãs brancas, que compõe 99,9% da massa das estrelas, nos modelos assumindo a seção de choque convencional da reação C(α,γ)O, é de
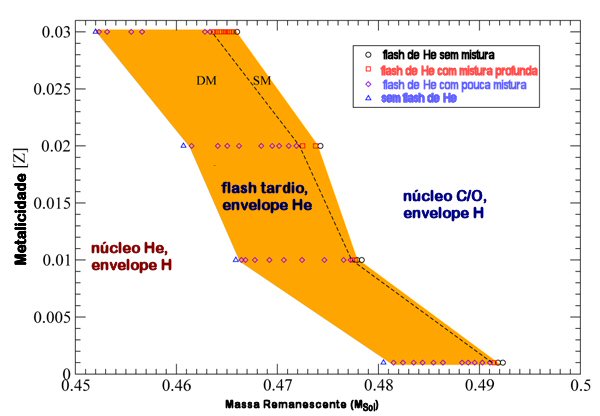
Existem poucas anãs brancas com massas medidas por astrometria ou sismologia:
As massas sismológicas foram obtidas por Donald Earl Winget (1955-), Steven Daniel Kawaler (1958-), R. Edward Nather (1926-2014), Kepler de Souza Oliveira Filho (1956-), José Eduardo da Silveira Costa, e seus colaboradores do Whole Earth Telescope.
Como vimos anteriormente, a
massa de Chandrasekhar,
é a massa máxima que uma estrela anã branca pode ter,
e ser suportada por pressão degenerada dos elétrons.
As duas estrelas não binárias de mais alta massa, inferidas
espectroscopicamente, são
PG1658+441, com
![]() ,
massa
,
massa
![]() e
e
![]() K, e
GD 50, com
K, e
GD 50, com
![]() e massa
e massa
![]() .
Kepler et al. (2007) publicaram outras com
até 1,33 MSol.
Todas estão abaixo do limite de 1,38 MSol,
a massa de
Chandrasekhar para um núcleo de O/Ne/Mg, a composição
do núcleo mais
provável.
.
Kepler et al. (2007) publicaram outras com
até 1,33 MSol.
Todas estão abaixo do limite de 1,38 MSol,
a massa de
Chandrasekhar para um núcleo de O/Ne/Mg, a composição
do núcleo mais
provável.
Com a descoberta de que mais de 4% das anãs brancas têm campos magnéticos entre 1 MG e 1 GG (Kepler et al. 2013, Montly Notices of the Royal Astronomical Society), é importante estudar o efeito destes campos magnéticos na estrutura das anãs brancas, usando a Equação de Estado calculada por Alexander Y. Potekhin e Gilles Chabrier, 2012 e 2014, por exemplo, que levam a massas de Chandrasekhar de até 2,8 massas solares, segundo os cáculos de Upasana Das e Banibrata Mukhopadhyay, publicados em 2012 no Physical Review D, 86,2001, que argumentam que as supernovas Ia peculicares SN2006gz, SN2007if, SN2009dc e SN2003fg parecem indicar massas de anãs brancas tão altas. Isto ocorre porque o teorema do virial escalar torna-se,
A maior parte das
estrelas anãs brancas com massas acima de
![]() provavelmente passou pela fase de
nebulosa planetária, mas em geral 30% das anãs brancas
não são descendentes das nebulosas planetárias. Somente
cerca de
2% das anãs brancas evoluíram diretamente do ramo horizontal
e os 28% restantes vêm igualmente do ramo gigante assintótico
e da evolução de sistemas binários interagentes.
provavelmente passou pela fase de
nebulosa planetária, mas em geral 30% das anãs brancas
não são descendentes das nebulosas planetárias. Somente
cerca de
2% das anãs brancas evoluíram diretamente do ramo horizontal
e os 28% restantes vêm igualmente do ramo gigante assintótico
e da evolução de sistemas binários interagentes.
Em termos de sua composição atmosférica, as anãs brancas se dividem basicamente em duas classes:
Arun Mathew & Malay Kumar Nandy, no artigo arXiv:1807.01731, Noncommutative dispersion relation and mass-radius relation of white dwarfs, discutem as correções quânticas e a neutronização na massa de Chandrasekhar.