| Estrelas de Nêutrons |
Multiplicando (1.102) por ![]() , podemos integrá-la, resultando em:
, podemos integrá-la, resultando em:
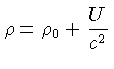
Diferenciando a equação (1.100) em relação a ![]() ,
obtemos
,
obtemos
![]() em função de
em função de
![]() .
Podemos eliminar
.
Podemos eliminar
![]() utilizando as equações (1.100), (1.101)
e (1.102),
chegando à equação de
Tolman-Oppenheimer-Volkoff para o equilíbrio
hidrostático na relatividade geral:
utilizando as equações (1.100), (1.101)
e (1.102),
chegando à equação de
Tolman-Oppenheimer-Volkoff para o equilíbrio
hidrostático na relatividade geral:
De acordo com George William Collins II (1937-),
em The Fundamentals of Stellar Astrophysics, 1989, (New York: Freeman),
um modelo simples é
![]() .
A equação da continuidade da massa
.
A equação da continuidade da massa
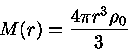
![\frac{dP(r)}{dr}= -\frac{4\pi Gr\rho_0^2[1+P/(\rho_0 c^2)][1+3P/(\rho_0 c^2)]} {3[1-8\pi G\rho_0 r^2/(3c^2)]}](relat/img4.gif)
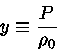
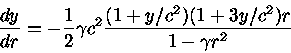
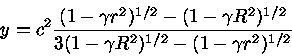
![P(r)=\rho_0 c^2 \frac{[1-2GMr^2/(R^3c^2)]^{1/2} -[1-2GM/(Rc^2)]^{1/2}} {3[1-2GM/(Rc^2)]^{1/2} -[1-2GMr^2/(R^3c^2)]^{1/2}}](relat/img10.gif)
![P_c=\rho_0 c^2 \frac{1-[1-2GM/(Rc^2)]^{1/2}} {3[1-2GM/(Rc^2)]^{1/2}-1}](relat/img11.gif)
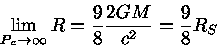
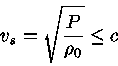
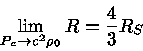
A verdadeira equação de estado das estrelas de nêutrons ainda não é conhecida,
já que não sabemos como descrever a força forte,
mas Edwin Salpeter (1925-2008)
(1961, Astrophysical Journal, 134, 669) mostrou que,
para um gás de elétrons e
núcleos atômicos de peso atômico A e carga Z, com
![]() = A/Z,
incluindo os efeitos Coulombianos da rede de íons,
as correções de Thomas-Fermi
[Llewellyn H. Thomas (1903-1992) The calculation of atomic fields,
Proceedings of the
Cambridge Philosophical Society, 23, 542-548, 1927;
Enrico Fermi (1901-1954).
Un metodo statistice per la determinazione di alcune proprieta del
l'atomo. Rendiconti Accademia Nazionale dei Lincei, 6, 602-607, 1927]
para a não uniformidade da
distribuição de elétrons
(escudamento eletrônico), energia de troca e interações
spin-spin dos
elétrons,
podemos escrever a equação de forma paramétrica como
= A/Z,
incluindo os efeitos Coulombianos da rede de íons,
as correções de Thomas-Fermi
[Llewellyn H. Thomas (1903-1992) The calculation of atomic fields,
Proceedings of the
Cambridge Philosophical Society, 23, 542-548, 1927;
Enrico Fermi (1901-1954).
Un metodo statistice per la determinazione di alcune proprieta del
l'atomo. Rendiconti Accademia Nazionale dei Lincei, 6, 602-607, 1927]
para a não uniformidade da
distribuição de elétrons
(escudamento eletrônico), energia de troca e interações
spin-spin dos
elétrons,
podemos escrever a equação de forma paramétrica como
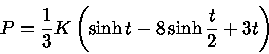
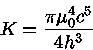
![t=4\log{\frac{\hat{p}}{\mu_0 c}+[1+(\frac{\hat{p}}{\mu_0 c})^2]^{1/2}}](relat/img21.gif)
Subrahmanyan Chandrasekhar (1910-1995) e Robert F. Tooper (1964, Astrophysical Journal, 183, 941) demontraram que as anãs brancas colapsam por efeitos da relatividade geral com 98% da massa de Chandrasekhar. Para as estrelas de nêutrons, a relatividade geral causa o colapso muito antes de toda a estrela tornar-se relativisticamente degenerada.
Nas estrelas de nêutrons, os elétrons degenerados têm energia suficiente para induzir o decaimento ![]() inverso, isto é,
colidir com um próton formando um nêutron. O subsequente decaimento
inverso, isto é,
colidir com um próton formando um nêutron. O subsequente decaimento ![]() não é possível porque implicaria na emissão de um próton e
um elétron de menor energia e, portanto, em um estado já completamente ocupado.
não é possível porque implicaria na emissão de um próton e
um elétron de menor energia e, portanto, em um estado já completamente ocupado.
Desta maneira prótons são convertidos em nêutrons, formando núcleos ricos em nêutrons. Neste caso, a repulsão coulombiana é reduzida e núcleos mais pesados que o 56Fe são formados.
Podemos estimar a densidade média de uma estrela de nêutrons, considerando
que a massa média é de 1,4 ![]() e raio de 10 km
e raio de 10 km
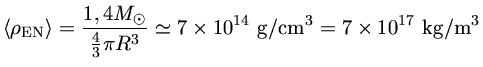
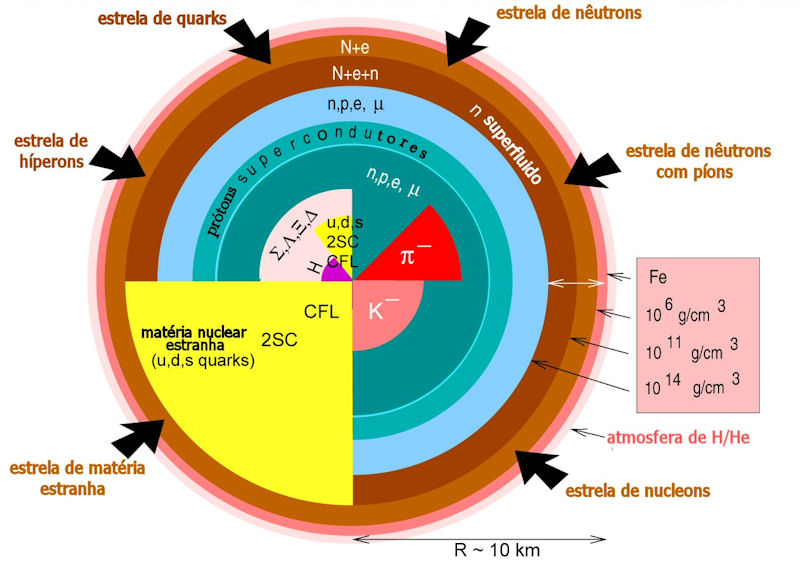
Para densidades superiores, os núcleos começam a se unir, formando um denso gás de elétrons, prótons e nêutrons. A equação de estado depende então fortemente da interação entre os núcleons, ainda incerta. Para densidades de
![]() , píons, múons e híperons são energeticamente possíveis, e acima disto, os quarks tornam-se importantes.
A coexistência em equilíbrio de nêutrons, prótons e elétrons,
para temperatura desprezável, é caracterizada por
, píons, múons e híperons são energeticamente possíveis, e acima disto, os quarks tornam-se importantes.
A coexistência em equilíbrio de nêutrons, prótons e elétrons,
para temperatura desprezável, é caracterizada por
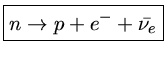 e
e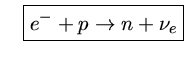
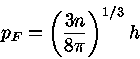
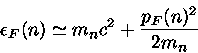
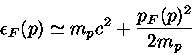
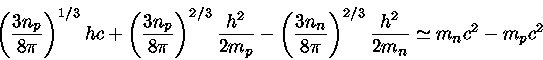
Para estrelas de nêutron, as densidades são maiores que
as da matéria nuclear.
Neste caso,
a Energia de Fermi é da ordem de
![]() MeV, correspondendo
a
MeV, correspondendo
a
![]() K. Portanto a energia cinética
devido a degenerescência é a principal contribuição
à pressão, com correções substanciais devido às forças
nucleares. A agitação térmica é desprezável,
já que a emissão de neutrinos no colapso para estrela de nêutrons
esfria o núcleo para
K. Portanto a energia cinética
devido a degenerescência é a principal contribuição
à pressão, com correções substanciais devido às forças
nucleares. A agitação térmica é desprezável,
já que a emissão de neutrinos no colapso para estrela de nêutrons
esfria o núcleo para
![]() K em poucos segundos.
O processo mais eficiente de formação de neutrinos é o processo URCA
(
K em poucos segundos.
O processo mais eficiente de formação de neutrinos é o processo URCA
(![]() e
e
![]() ),
e Urca modificado
(
),
e Urca modificado
(![]() e
e
![]() ),
que é proporcial a T8, esfriando a estrela rapidamente para
T<109K.
Após algo entre 10 a 10 000 anos, o processo URCA torna-se
ineficiente, e esfriamento por bremsstrahlung de pares de neutrinos
e mais tarde por emissão térmica de fótons esfria a estrela e leva a
uma temperatura superficial de alguns milhões de Kelvin.
Mas se o núcleo não for composto por matéria normal, o esfriamento
pode ser mais complicado.
),
que é proporcial a T8, esfriando a estrela rapidamente para
T<109K.
Após algo entre 10 a 10 000 anos, o processo URCA torna-se
ineficiente, e esfriamento por bremsstrahlung de pares de neutrinos
e mais tarde por emissão térmica de fótons esfria a estrela e leva a
uma temperatura superficial de alguns milhões de Kelvin.
Mas se o núcleo não for composto por matéria normal, o esfriamento
pode ser mais complicado.
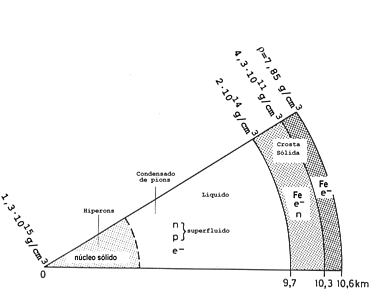
Desta forma, estranheza não é conservada em objetos astrofísicos.
Nos núcleos atômicos estáveis, a massa dos híperons é maior do que
a energia de Fermi, de modo que não é energeticamente favorável
a transformação em híperons. As reações nucleares são tão rápidas
![]()
![]() 10-22 s, que a estranheza é conservada nesta escala de
tempo. Desta forma, embora a matéria nuclear normal tenha estranheza
líquida zero, as estrelas de nêutrons podem ter, e quase certamente têm,
híperons e ter estranheza líquida não nula.
(Norman K. Glendenning, 1997, Compact Stars, Springer: New York.)
10-22 s, que a estranheza é conservada nesta escala de
tempo. Desta forma, embora a matéria nuclear normal tenha estranheza
líquida zero, as estrelas de nêutrons podem ter, e quase certamente têm,
híperons e ter estranheza líquida não nula.
(Norman K. Glendenning, 1997, Compact Stars, Springer: New York.)
A primeira derivação do colapso de uma estrela para o estágio de buraco negro foi publicada por Julius Robert Oppenheimer (1904-1967) e Hartland Snyder em 1939, no Physical Review, 56, demonstrando que o último estágio do colapso é um buraco negro, e que a estrela corta qualquer comunicação com o exterior. Em 1974 o físico inglês Stephen W. Hawking (1942-) demonstra que os efeitos de tunelamento quântico levam à evaporação de qualquer buraco negro, em escalas de tempo suficientemente grandes. Para um tratamento adequado do assunto, veja o livro Compact Stars, do físico Norman K. Glendenning, publicado pela Springer em 1997, ou as notas de Edward Lewis Robinson (1945-), Black Holes, que deduz o espaço-tempo de Kerr [Roy P. Kerr (1934-)] fora de um buraco negro em rotação, publicado em 1963 no artigo "Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics", no Physics Review Letters, 11, 237, em coordenadas de Boyer-Lindquist [Robert H. Boyer e Richard W. Lindquist, "Maximal Analytic Extension of the Kerr Metric", Journal Mathematical Physics, 8, 265, 1967], uma generalização da métrica de Schwarzschild.
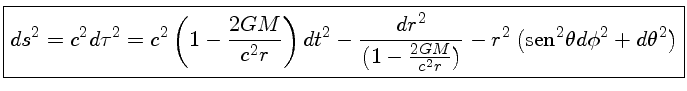 |
(Schwarzschild) |
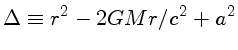
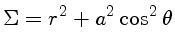
O pulsar PSR J1748-2446 tem um período de rotação de 1,39 ms. O tensor energia-momentum consiste do tensor do gás ideal adicionado ao tensor eletromagnetico.
Kuantay Boshkayev, Jorge A. Rueda, Remo Ruffini & Ivan Siutsou, em seu
artigo On General Relativistic Uniformly Rotating White Dwarfs,
publicado em 2013 no Astrophysical Journal, 762, 117,
calcularam o limite de 1,467 MSol e período
de rotação máximo de 0,7 s, para uma anã
branca de oxigênio.
Pablo Marchant, Andreas Reisenegger, Juan Alejandro Valdivia & Jaime H. Hoys,
no artigo de 2014 Stability of Hall Equilibria in Neutron Stars, arXiv 1410.5833v1,
explicam que
na crosta das estrelas de nêutrons, os íons estão presos numa estrutura cristalina, e
somente os elétrons estão livres. Eles estudam o efeito da estrutura do campo magnético
na dissipação deste por oscilações amortecidas, devido ao efeito Hall, descoberto em
1879 por Edwin Herbert Hall (1855-1938), em que cargas elétricas movendo-se em um campo magnético
perpendicular à corrente se curvam devido à força de Lorentz, acumulando-se na superfície e gerando
um campo elétrico que se opõe ao movimento,
e devido ao efeito Ohmico, de perda de energia pela resistência do material.
Sebastien Guillot e Robert E. Rutledge, astroph 1409.4306v1, assumem que todas as estrelas de
nêutrons dentro de binárias de baixa massa quiecentes em raio-X (qLMXBs) têm o mesmo raio,
e ajustam o espectro térmico observado com um modelo com atmosfera de hidrogênio em
seis sistemas pertencentes a aglomerados globulares galácticos, obtendo
REN=9.4±1,2 km, o que os leva a restringir várias equações de
estado para a matéria nuclear.
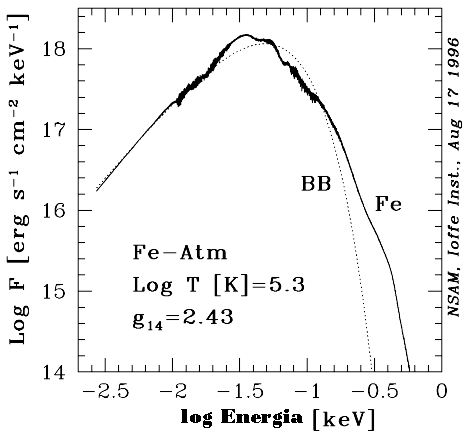
A espessura da atmosfera da estrela de nêutrons pode ser estimada utilizando n(z)=n0e-z/H, com a escala de altura H=kT/mg, já que a há equilíbrio entre a força gravitacional e a pressão, kT. A escala de altura resultante é de apenas 0,13 cm, comparada com 8 km para a atmosfera da Terra. A densidade na atmosfera da estrela de nêutrons é 3,5 g/cm3, o que corresponde a carbono cristalino, de modo que a equação de estado não é de gás ideal.
Lukas R. Weih, Elias R. Most & Luciano Rezzolla, no artigo On the stability and maximum mass of differentially rotating relativistic stars, 2017, arXiv:1709.06058, obtiveram Mmax = (1,54 ± 0,05) MTOV, para todas as equações de estado que supuseram.
Equação de Estado para
o interior de estrelas de nêutrons, calculada por Alexander Yurievich Potekhin, do IOFFE.
Emanuele Berti, 2014, A Black Hole Primer