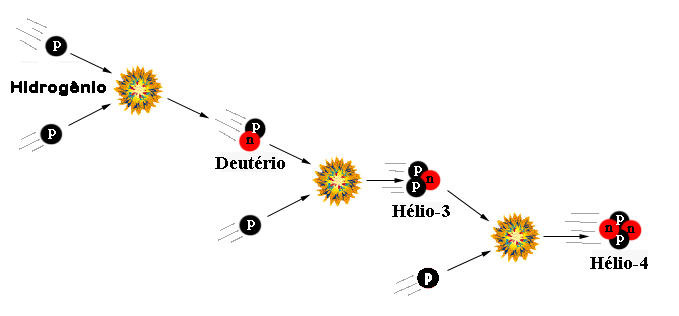
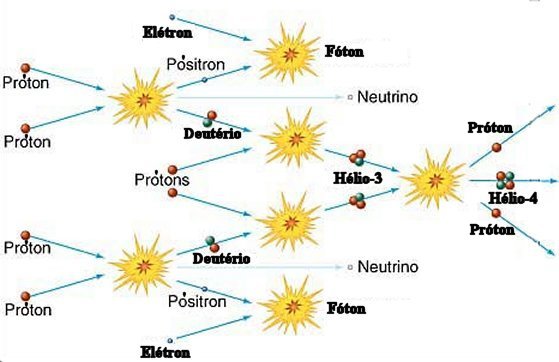
As cadeias são:
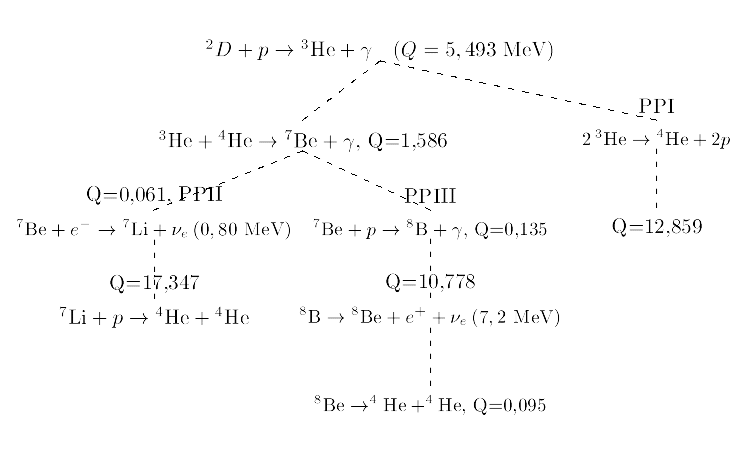
O ciclo PPI tem ![]() Mev, com
dois neutrinos de energia média de 0,263 Mev cada
(0,42 MeV máxima), enquanto o PPII tem
Mev, com
dois neutrinos de energia média de 0,263 Mev cada
(0,42 MeV máxima), enquanto o PPII tem ![]() Mev, correspondendo a uma perda por
neutrinos de 4%, com neutrinos de 0,80 Mev, além dos dois de
0,263 Mev. O ciclo PPIII, com
Mev, correspondendo a uma perda por
neutrinos de 4%, com neutrinos de 0,80 Mev, além dos dois de
0,263 Mev. O ciclo PPIII, com ![]() Mev, corresponde a uma perda por neutrinos
de 28%, com neutrinos carregando 7,2 Mev, além dos dois de
0,263 Mev.
Mev, corresponde a uma perda por neutrinos
de 28%, com neutrinos carregando 7,2 Mev, além dos dois de
0,263 Mev.
Com uma média de energia por reação de 25 Mev ![]() ergs/ciclo, uma luminosidade
solar de
ergs/ciclo, uma luminosidade
solar de ![]() ergs/s,
obtemos um total de neutrinos de:
ergs/s,
obtemos um total de neutrinos de:
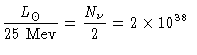 neutrinos/segundo
neutrinos/segundo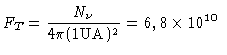
Entretanto, como a secção de choque do neutrino é da ordem de:
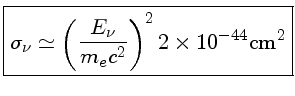
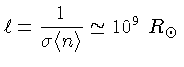
 Os neutrinos foram previstos teoricamente por
Wolfgang Pauli (1900-1958)
em 1930, para explicar a variação da energia dos
elétrons emitidos em decaimentos β,
em que um
nêutron se transforma espontâneamente em um
próton, emitindo um elétron.
A vida média de um nêutron livre é de aproximadamente 12 minutos.
Pauli propôs que
a diferença de energia estava sendo carregada por
uma partícula neutra de difícil detecção,
o neutrino. Ele recebeu o prêmio Nobel em 1945.
Os neutrinos foram previstos teoricamente por
Wolfgang Pauli (1900-1958)
em 1930, para explicar a variação da energia dos
elétrons emitidos em decaimentos β,
em que um
nêutron se transforma espontâneamente em um
próton, emitindo um elétron.
A vida média de um nêutron livre é de aproximadamente 12 minutos.
Pauli propôs que
a diferença de energia estava sendo carregada por
uma partícula neutra de difícil detecção,
o neutrino. Ele recebeu o prêmio Nobel em 1945.
 Em 1956 os neutrinos foram finalmente detectados
por
Frederick Reines (1918-1998)
e Clyde L. Cowan Jr (1919-1974),
emitidos de um reator nuclear
["The Neutrino", Frederick Reines &
Clyde L. Cowan, Jr., Nature 178, 446 (1956);
"Detection of the Free Neutrino: A Confirmation",
Clyde L. Cowan, Frederick Reines, Francis B. Harrison,
Herald W. Kruse, & Austin D. McGuire, Science, 124, 103 (1956)].
Reines recebeu o prêmio
Nobel em 1995 pela descoberta.
Neutrinos produzidos no núcleo do Sol saem ao espaço
com muito pouca interação, atravessam a distância
entre o Sol e a Terra, e na maioria dos casos passam pela
Terra sem qualquer perturbação. Milhões destes
neutrinos passam por nosso corpo a todo segundo, mas durante
nossa vida inteira somente alguns destes interagirão com
nossos átomos. O mais importante é que os neutrinos
carregam informação sobre o interior do Sol, onde
a energia está sendo gerada.
Em 1956 os neutrinos foram finalmente detectados
por
Frederick Reines (1918-1998)
e Clyde L. Cowan Jr (1919-1974),
emitidos de um reator nuclear
["The Neutrino", Frederick Reines &
Clyde L. Cowan, Jr., Nature 178, 446 (1956);
"Detection of the Free Neutrino: A Confirmation",
Clyde L. Cowan, Frederick Reines, Francis B. Harrison,
Herald W. Kruse, & Austin D. McGuire, Science, 124, 103 (1956)].
Reines recebeu o prêmio
Nobel em 1995 pela descoberta.
Neutrinos produzidos no núcleo do Sol saem ao espaço
com muito pouca interação, atravessam a distância
entre o Sol e a Terra, e na maioria dos casos passam pela
Terra sem qualquer perturbação. Milhões destes
neutrinos passam por nosso corpo a todo segundo, mas durante
nossa vida inteira somente alguns destes interagirão com
nossos átomos. O mais importante é que os neutrinos
carregam informação sobre o interior do Sol, onde
a energia está sendo gerada.
 Em 1968, Raymond Davis Jr. (1914-2006) e seus colaboradores,
do Brookhaven National Laboratories, decidiram
detectar estes neutrinos colocando um tanque
com 378 000 litros de fluído
de limpeza percloroetileno (C2Cl4),
do tamanho de um vagão de trem, no fundo de uma
mina de ouro a 1500m de profundidade na cidade de Lead,
na Dakota do Sul, para evitar a contaminação por
raios cósmicos. Como aproximadamente
um quarto dos átomos de cloro está no isótopo 37,
ele calculou que dos 100 bilhões
de neutrinos solares que
atravessam a Terra por segundo, alguns ocasionalmente interagiriam
com um átomo de cloro, transformando-o em um átomo
de argônio. Como o argônio37
produzido é radiativo,
com vida média de 35 dias, é possível isolar
e detectar estes poucos átomos de argônio dos mais
de 1030
átomos de cloro no tanque.
Periodicamente o número de átomos
de argônio no tanque seria medido, determinando o
fluxo de neutrinos.
Em 1968, Raymond Davis Jr. (1914-2006) e seus colaboradores,
do Brookhaven National Laboratories, decidiram
detectar estes neutrinos colocando um tanque
com 378 000 litros de fluído
de limpeza percloroetileno (C2Cl4),
do tamanho de um vagão de trem, no fundo de uma
mina de ouro a 1500m de profundidade na cidade de Lead,
na Dakota do Sul, para evitar a contaminação por
raios cósmicos. Como aproximadamente
um quarto dos átomos de cloro está no isótopo 37,
ele calculou que dos 100 bilhões
de neutrinos solares que
atravessam a Terra por segundo, alguns ocasionalmente interagiriam
com um átomo de cloro, transformando-o em um átomo
de argônio. Como o argônio37
produzido é radiativo,
com vida média de 35 dias, é possível isolar
e detectar estes poucos átomos de argônio dos mais
de 1030
átomos de cloro no tanque.
Periodicamente o número de átomos
de argônio no tanque seria medido, determinando o
fluxo de neutrinos.
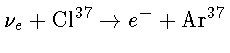
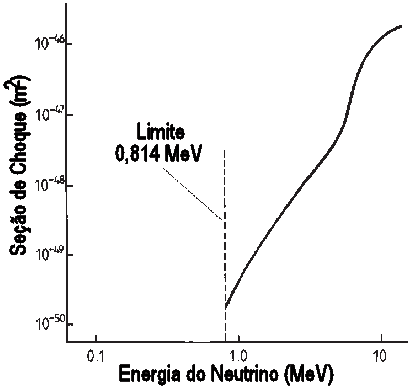 A dificuldade maior do experimento de Davis
é que ele só consegue detectar neutrinos com
energia maior que 0,81 MeV
e, portanto, não consegue detectar o neutrino produzido
na cadeia principal do ciclo p-p,
dominante no Sol,
pois este neutrino só tem 0,42 MeV de energia
e tem um fluxo de 6,4 × 1010 neutrinos/cm2/s aqui na Terra.
A dificuldade maior do experimento de Davis
é que ele só consegue detectar neutrinos com
energia maior que 0,81 MeV
e, portanto, não consegue detectar o neutrino produzido
na cadeia principal do ciclo p-p,
dominante no Sol,
pois este neutrino só tem 0,42 MeV de energia
e tem um fluxo de 6,4 × 1010 neutrinos/cm2/s aqui na Terra.
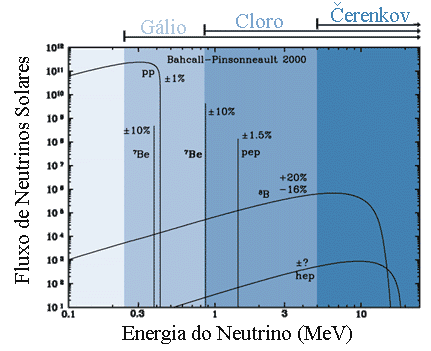
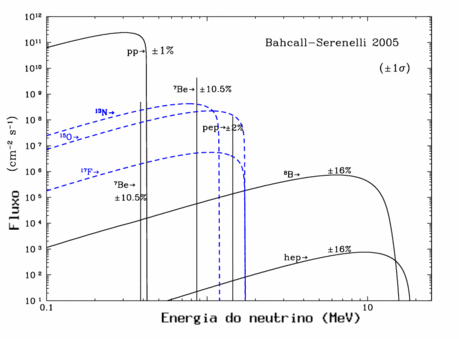
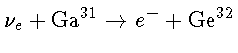
| Experimento | fluxo medido (SNU) | razão medida/teoria (sem oscilação na teoria) | energia mínimia | Anos de operação |
|---|---|---|---|---|
| Davis (Cloro) | 2,56± 0,1± 0,16 | 0,33 ± 0,03± 0,05 | 0,814 MeV | 1970-1995 |
| Kamiokande (Cerenkov) | 2,80 ± 0,19 ± 0,33 | 0,54 ± 0,08 +0,10-0,07 | 7,5 MeV | 1986-1995 |
| SAGE (Gálio) | 65 ± 3 ± 3 | 0,50 ± 0,06 ± 0,03 | 0,233 MeV | 1990-2007 |
| Gallex (Gálio) | 78 ± 6 ± 5 | 0,60 ± 0,06 ± 0,04 | 0,233 MeV | 1991-1997 |
| Super-Kamiokande | 2,32 ± 0,04 ± 0,05 | 0,464 ± 0,005 ± 0,015 | 5.0-20 MeV | 1996-2010 |
| GNO (Gálio) | 69,3 ± 5,5 | 0,51 ± 0,08 ± 0,03 | 0,233 MeV | 1998-2003 |
| SNO (Cerenkov) |
1,68 ± 0,06 ± 0,05 (CC) 2,35 ± 0,22 ± 0,15 (ES) 4,94 ± 0,21 ± 0,36 (NC) |
0,346 ± 0,029 (CC) | 6,75 MeV | 1999-2006 |
| SNU = 10-36 capturas/alvo/s - CC=charged current - ES=electron scattering - NS=neutral current | ||||
Ko Abe e colaboradores publicaram em 2011,
no
Physical Review D, 83, 052010, os resultados dos
dados de 2002 a 2010, com um total de 8132 neutrinos detectados.
Os pesquisadores concluíram, com
um nível de confiança de 99,99%,
que a não detecção dos neutrinos faltantes somente é consistente
com a oscilaçao de neutrinos, isto é, na transformação dos neutrinos,
após produzidos e antes de serem detectados, de neutrinos de
elétrons para neutrinos de múons ou de táons, com
Maria Concepion Gonzalez-Garcia, Michele Maltoni e Jordi Salvado, no
artigo de revisão de 2011
Updated global fit to three neutrino mixing: status of the hints of θ1,3>0,
discutem que ainda não há provas suficientes de que o neutrinos dos elétrons e táons se misturam diretamente.
O A produção do oxigênio, por acréscimo de outra partícula
A reação
![]() m2,1=7,6±0,02 meV,
com ângulo de mistura sen2θ1,2=0,31±0,01,
enquanto sen2θ1,3<0,060 com 95% de confiança.
Nesta nomenclatura, 1=νe, 2=νμ e 3=ντ.
m2,1=7,6±0,02 meV,
com ângulo de mistura sen2θ1,2=0,31±0,01,
enquanto sen2θ1,3<0,060 com 95% de confiança.
Nesta nomenclatura, 1=νe, 2=νμ e 3=ντ.
Construir detectores maiores do que o SuperKamiokande não é prático,
mas grandes quantidades de água podem ser monitoradas usando lagos
ou a calota polar Antártica, como os detectores NT-220,
Antares, Nestor e IceCube. Antares monitora 1 milhão de litros
de água com 900 fotomulticadoras a 4000 metros de profundidade
no Peloponésio, e o IceCube usa 5160 fotomultiplicadoras
em 80 cordas monitorando 1000 milhões de metros cúbicos (1 km3)
de gelo na Antártica. O IceCube ficou pronto em Maio/2011 e foi construído para detectar neutrinos
mais energéticos que 100 GeV, mas devido ao baixo ruído é capaz de detectar
até MeV.

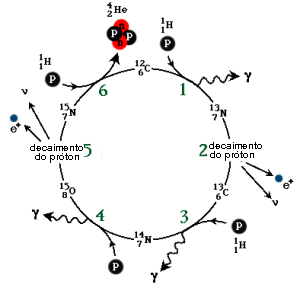
Ciclo CNO
O ciclo CNO domina a queima de hidrogênio para ![]() K, usando o C e N como
catalisadores, com
K, usando o C e N como
catalisadores, com ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ou, com menor probabilidade:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
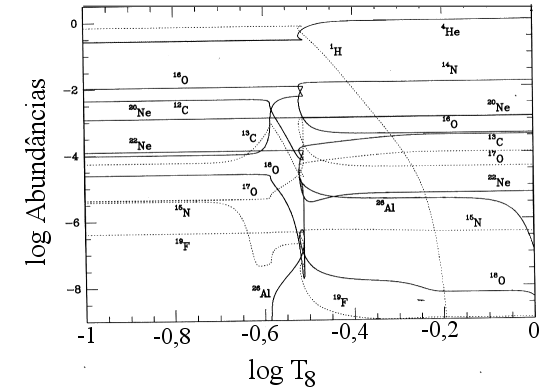
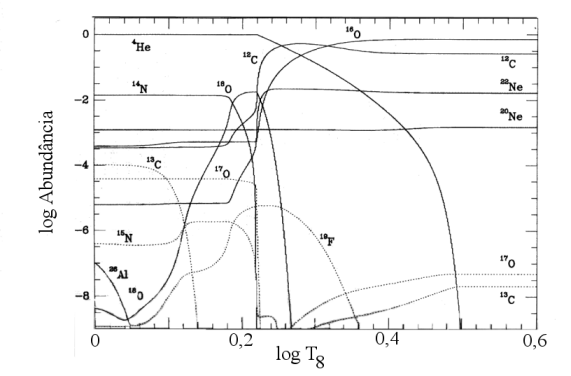
Evolução das abundâncias com a temperatura do núcleo para uma
estrela com massa inicial de aproximadamente 25 MSol.
T8=T/108.Triplo-α
A reação triplo
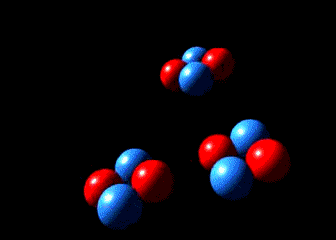
Três átomos de hélio colidem, formando um carbono e liberando fótons.
Esta reação só ocorre eficientemente para T>100 milhões de K.
O 8Be formado na colisão de duas partículas
α, decai em 6,7×10-17s novamente em dois
núcleos de He.
![]() foi proposta pelo americano
Edwin Ernest Salpeter (1924-2008), fundindo três núcleos de hélio
(partículas α)
em um núcleo de carbono.
foi proposta pelo americano
Edwin Ernest Salpeter (1924-2008), fundindo três núcleos de hélio
(partículas α)
em um núcleo de carbono.  Existe uma resonância no núcleo composto do carbono, 7,65 MeV acima
do estado fundamental, que permite que esta reação ocorra com taxas
significativas, conforme predito por Sir Fred Hoyle
(1915-2001) e posteriormente observada.
Existe uma resonância no núcleo composto do carbono, 7,65 MeV acima
do estado fundamental, que permite que esta reação ocorra com taxas
significativas, conforme predito por Sir Fred Hoyle
(1915-2001) e posteriormente observada.
Para temperaturas acima de ![]() K, ocorre a queima do hélio, pelo
processo chamado
triplo-
K, ocorre a queima do hélio, pelo
processo chamado
triplo-![]() ,
com
,
com ![]() :
:
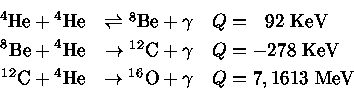
![]() decai em 2
decai em 2 ![]() em um
tempo de vida médio de 0,067 fentosegundos.
em um
tempo de vida médio de 0,067 fentosegundos.![]() ao
ao
![]() C
C![]() O,
só ocorre porque o
princípio da incerteza permite que uma resonância com energia um
pouco abaixo do limite ocorra, quando classicamente seria proibida.
A próxima reação,
O,
só ocorre porque o
princípio da incerteza permite que uma resonância com energia um
pouco abaixo do limite ocorra, quando classicamente seria proibida.
A próxima reação,
![]() O
O![]() Ne
é lenta para estas
temperaturas, mas
Ne
é lenta para estas
temperaturas, mas
![]() N
N![]() F
ocorre, seguida do decaimento de 18F para
18O. Acima de 6×108 K temos
F
ocorre, seguida do decaimento de 18F para
18O. Acima de 6×108 K temos
![]() O
O![]() Ne,
Ne,
![]() Ne
Ne![]() Mg
e, com menor probabilidade,
Mg
e, com menor probabilidade,
![]() Ne
Ne![]() Mg.
domina a produção de nêutrons nas camadas externas,
de acordo com Roberto Gallino et al. 1998, Astrophysical Journal, 497, 338.
Durante a queima de
hélio o processo s (slow) de lenta captura de
nêutrons, produzidos nas reações com
13C,
13N e
22Ne,
ocorre em estrelas
massivas, produzindo os núcleons até o chumbo. Para as estrelas de
massa entre 1 e 8 MSol um forte processo s
ocorre por interação entre as camadas que queimam hidrogênio e
hélio.
Mg.
domina a produção de nêutrons nas camadas externas,
de acordo com Roberto Gallino et al. 1998, Astrophysical Journal, 497, 338.
Durante a queima de
hélio o processo s (slow) de lenta captura de
nêutrons, produzidos nas reações com
13C,
13N e
22Ne,
ocorre em estrelas
massivas, produzindo os núcleons até o chumbo. Para as estrelas de
massa entre 1 e 8 MSol um forte processo s
ocorre por interação entre as camadas que queimam hidrogênio e
hélio.![]() C
C![]() N
N![]() C
C![]() O
O
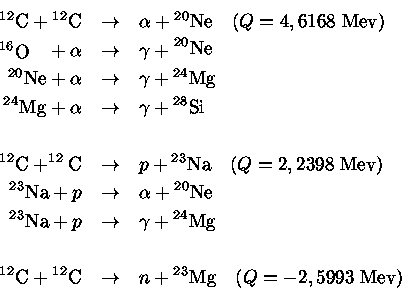
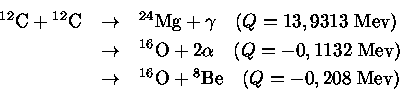
Para T=1- ![]() K:
K:
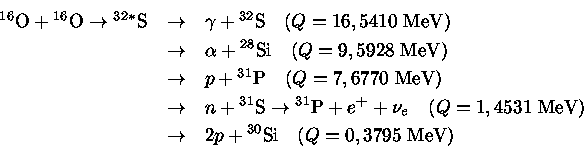
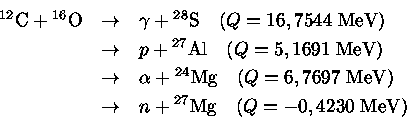
![]()
| Processo | Q NA/A (MeV/nucleon) |
| 5 a 7 | |
| 0,606 | |
| 0,902 | |
| 0,52 | |
| 0,11 | |
| 0,52 | |
| 0 a 0,31 |
William Alfred Fowler (1911-1995) e Sir Fred Hoyle
(1915-2001) propuseram em 1964, no Astrophysical Journal
Supplements, 9, 201, que o processo de queima do silício
preferencialmente sintetiza o 56Ni porque a rápida
queima não permite decaimentos
![]() suficientes para produzir o 56Fe. Decaimentos
suficientes para produzir o 56Fe. Decaimentos
![]() posteriores, enquanto a matéria ainda
está quente, formam o 56Fe. A solução da cadeia de
reações simultaneas por James Wellington Truran, David Arnett
(1940-) e Alastair G.W. Cameron (1925-), 1967, Canadian Journal of
Physics, 45, 2315, demonstra que o 56Ni é realmente
dominante para matéria pouco abundante em nêutrons. Se os
nêutrons são abundantes, o núcleo dominante passa para o
54Fe, 56Fe e finalmente 58Fe, com
o aumento do número de nêutrons. O fluxo de nêutrons depende da
metalicidade do material.
posteriores, enquanto a matéria ainda
está quente, formam o 56Fe. A solução da cadeia de
reações simultaneas por James Wellington Truran, David Arnett
(1940-) e Alastair G.W. Cameron (1925-), 1967, Canadian Journal of
Physics, 45, 2315, demonstra que o 56Ni é realmente
dominante para matéria pouco abundante em nêutrons. Se os
nêutrons são abundantes, o núcleo dominante passa para o
54Fe, 56Fe e finalmente 58Fe, com
o aumento do número de nêutrons. O fluxo de nêutrons depende da
metalicidade do material.
![]()
![]()
![]()
![]()
![]()
Próxima: Condição de Equilíbrio Térmico Volta:
Energia
Nuclear Anterior: Algumas Relações
Termodinâmicas