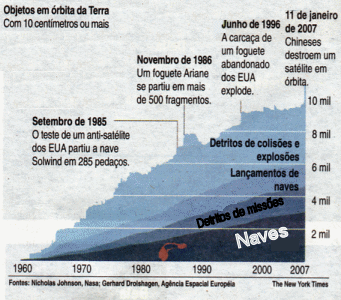

Desde o primeiro satélite artificial, o Sputnick, lançado pela União Soviética em 1957, com 83 kg e que alcançava altitude entre 225 e 950 km, cerca de 7560 satélites artificiais estão orbitando a Terra. Muitos satélites e foguetes lançados explodiram, dando origem a mais de 40,5 mil detritos espaciais maiores que 10 cm, 1,1 milhão de fragmentos entre 1 cm e 10 cm, e 130 milhões menores que 1 cm, que não podem ser detectados por radares aqui na Terra. Estes fragmentos constituem o lixo espacial. Cerca de 36,8 mil fragmentos maiores são monitorados aqui da Terra, porque podem causar sérios danos às naves e satélites, tripulados ou não.


4) Qual é a velocidade de um satélite em órbita circular a 300 km de altura sobre a Terra?
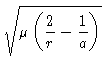 ,
,
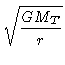 = 7, 5 km/s.
= 7, 5 km/s.
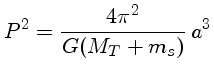 ∴ P=90 minutos.
∴ P=90 minutos.
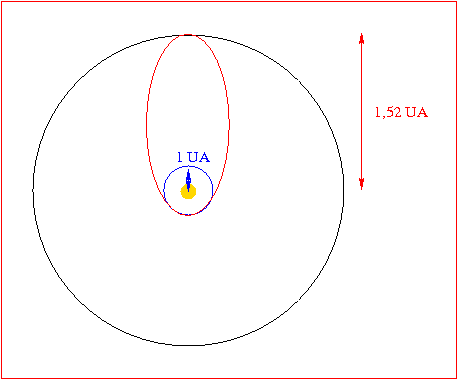
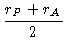 = 1, 26 UA,
= 1, 26 UA,
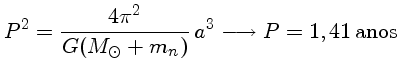
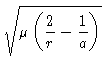 ,
,
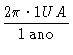
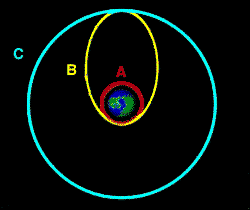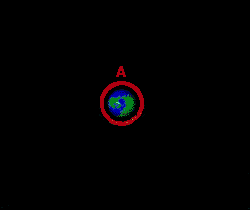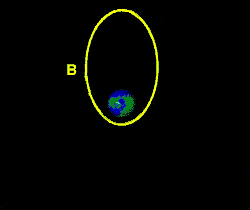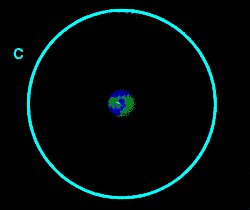 A manobra de Hohmann também é utilizada para lançar um satélite
em órbita geocêntrica a partir de uma órbita de baixa altitude,
primeiro colocando o satélite em uma órbita elipsoidal com distância
geocêntrica igual a da órbita desejada e depois circularizando a órbita.
A manobra de Hohmann também é utilizada para lançar um satélite
em órbita geocêntrica a partir de uma órbita de baixa altitude,
primeiro colocando o satélite em uma órbita elipsoidal com distância
geocêntrica igual a da órbita desejada e depois circularizando a órbita.
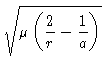 ,
,
7) Se quisermos enviar um satélite até a Lua ou qualquer outro planeta, precisamos primeiro vencer o campo gravitacional da Terra. Qual é a velocidade necessária para um satélite artificial escapar do campo gravitacional da Terra?
Como a massa do satélite pode ser desprezada em relação à massa da Terra:
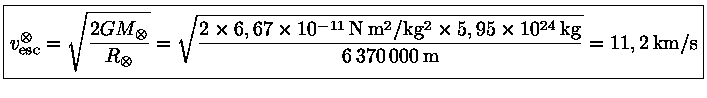
Um satélite artificial está sujeito à fricção com a atmosfera da Terra, causando o decaimento da órbita. Se o satélite se encontrar abaixo de 160 km da superfície da Terra, este decaimento dura somente alguns dias, e a desintegração ocorre a uma altitude de cerca de 80 km. Acima de 600 km, a fricção é tão pequena que a órbita geralmente dura mais do que 10 anos, ou seja, acima do tempo de vida operacional do satélite.
O método mais antigo usado para utilizar a gravidade como acelerador é a chamada transferência de Hohmann, proposta pelo engenheiro alemão Walter Hohmann (1880-1945): primeiro, impulsiona-se a nave com o foguete até uma órbita circular baixa em volta da Terra. Em seguida, aplica-se um impulso, com os motores da própria nave, que modifica a órbita: ela deixa de ser circular e se torna uma elipse alongada. Quando a nave se encontra no ponto mais alongado da elipse, aplica-se um novo impulso para colocá-la em uma nova órbita circular, só que bem mais alta que a primeira. É uma manobra cara porque os impulsos necessários são grandes e exigem grandes quantidades de combustível. A transferência de Hohmann serviu desde o início da era espacial para colocar satélites em orbita da Terra e até para enviar naves à Lua. Os progressos da Astrodinâmica têm mostrado como se deve proceder para aproveitar ao máximo a energia gravitacional durante os vôos espaciais. Hoje se analisa a atração gravitacional de vários corpos para descobrir quais são as trajetórias naturais existentes entre eles - ou seja, as rotas criadas pela gravidade e que as naves podem utilizar com vantagem. Se uma nave for lançada em uma trajetória adequada, ela pode seguir uma trajetória natural na qual não será necessário gastar nenhuma energia. A Mecânica Celeste mostra que existem pontos especiais, chamados pontos de Lagrange, nos quais a soma de várias atrações gravitacionais cria inúmeras possibilidades interessantes. Aí se cruzam infinitas trajetórias, bem diferentes uma da outra. E quando se dirige uma sonda para uma dessas regiões, basta um pequeno gasto de energia para alterar o seu movimento. É como se, no espaço houvessem superhighways interplanetarias, conectando os diversos pontos de Lagrange dos planetas do Sistema Solar. O problema é que essas trajetórias naturais são cheias de curvas e atalhos, que tornam as viagens demoradas. Ou seja, o que se ganha em energia, paga-se com tempo.
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)