Voltando para nossa equação do movimento
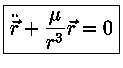
(1)
e multiplicando-se vetorialmente a equação de movimento (1) por
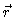 pela esquerda, temos:
Como o produto vetorial de qualquer vetor por si mesmo é nulo, já que o ângulo entre eles é zero e sen(0)=0,
pela esquerda, temos:
Como o produto vetorial de qualquer vetor por si mesmo é nulo, já que o ângulo entre eles é zero e sen(0)=0,
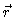 x
x 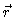
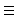 0,
o segundo termo acima é nulo e ficamos somente com o primeiro:
0,
o segundo termo acima é nulo e ficamos somente com o primeiro:
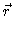 x
x 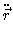
= 0.
Como
e
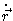 x
x 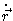
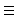 0, a equação acima implica
ou
o termo entre parêntesis deve ser uma constante, que
vamos chamar de momentum angular,
0, a equação acima implica
ou
o termo entre parêntesis deve ser uma constante, que
vamos chamar de momentum angular,
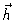 :
Esta é a lei da conservação do momentum angular.
:
Esta é a lei da conservação do momentum angular.
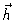 é o momentum angular por unidade de massa.
é o momentum angular por unidade de massa.
Note que
o vetor momento angular 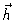 é sempre perpendicular
ao movimento, por sua definição (3).
é sempre perpendicular
ao movimento, por sua definição (3).
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)
Próxima: Primeira lei de Kepler: Lei das
Volta: Leis de Kepler Generalizadas
Anterior: Conservação da Energia Total do Sistema
©
Modificada em 1998-06-30
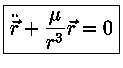 (1)
(1)
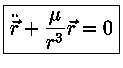 (1)
(1)
![]() é sempre perpendicular
ao movimento, por sua definição (3).
é sempre perpendicular
ao movimento, por sua definição (3).
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)