Próxima: Diferenciação Estatística Volta: Imagens Digitais Anterior: Soma de Imagens para Redução de

Filtragem

Filtragem digital é um conjunto de técnicas destinadas a corrigir e realçar uma imagem. A correção é a remoção de características indesejáveis, e a melhoria/realce é a acentuação de características.

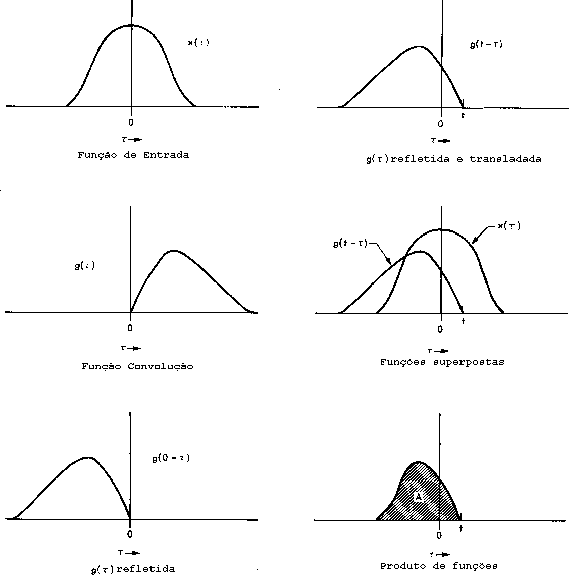
Chama-se de convolução o processo de calcular a intensidade de um determinado pixel em função da intensidade de seus vizinhos. O cálculo é baseado em ponderação, isto é, utilizam-se pesos diferentes para pixeis vizinhos diferentes. A matriz de pesos é chamada de kernel da convolução. Para obter o novo valor do pixel, multiplica-se o kernel pelo valor da imagem original em torno do pixel, elemento a elemento, e soma-se o produto, obtendo-se o valor do pixel na nova imagem.

Por exemplo, um filtro passa-baixa, que atenua as altas frequências da imagem, suavizando a imagem, e reduzindo o ruído, tem um kernel do tipo:

1/9	1/9	1/9
1/9	1/9	1/9
1/9	1/9	1/9

Para reduzir a quantidade de borramento, pode-se utilizar um kernel:

1/10	1/10	1/10
1/10	2/10	1/10
1/10	1/10	1/10

ou ainda um filtro gaussiano, que atenua ainda mais as altas frequências:

1/256	4/256	6/256	4/245	1/256
4/256	16/256	24/256	16/256	4/256
6/256	24/256	36/256	24/256	6/256
4/256	16/256	24/256	16/256	4/256
1/256	4/256	6/256	4/245	1/256

Um filtro passa-alta, que amplifica as altas frequências da imagem, realçando as partes de maior contraste, mas também amplificando o ruído:

-1	-1	-1
-1	9	-1
-1	-1	-1

ou

0	-1	0
-1	5	-1
0	-1	0

Um filtro de realce de bordas ou arestas (edge-enhancement), correspondente a deslocar a imagem e subtrair da imagem original:

-1	0	0
0	1	0
0	0	0

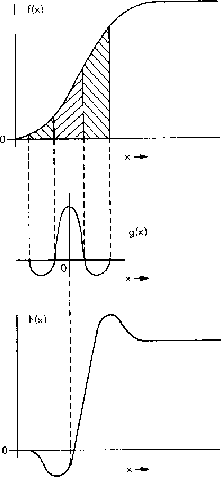
ou um filtro Laplaciano:

0	-1	0
-1	4	-1
0	-1	0

Para detecção de bordas, podemos usar o algoritmo de Sobel, que consiste em aplicar dois filtros diferentes à imagem original e calcular a soma dos quadrados:

$$\mathrm{imagem}_1 = \mathrm{imagem} \times \mathrm{Filtro}_1,$$

$$\mathrm{imagem}_2 = \mathrm{imagem} \times \mathrm{Filtro}_2,$$

$$\mathrm{imagem}_\mathrm{nova} = \sqrt{\mathrm{imagem}_1^2 + \mathrm{imagem}_2^2}.$$

$\mathrm{Filtro}_1$
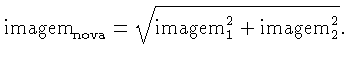
1	2	1
0	0	0
-1	-2	-1

$\mathrm{Filtro}_2$
1	0	-1
2	0	-2
1	0	-1

Próxima: Diferenciação Estatística Volta: Imagens Digitais Anterior: Soma de Imagens para Redução de