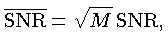Próxima: Filtragem
Volta: Imagens Digitais
Anterior: Registro
Podemos adicionar imagens para reduzir o ruído, se for possível
manter o paciente estacionário, já que o ruído, sendo
aleatório, cresce mais devagar que o sinal na soma.
Suponhamos que temos um conjunto de M imagens da forma:
onde 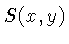 é o sinal de interesse, e
é o sinal de interesse, e  é o ruído
da imagem. Cada imagem é degradada por um ruído diferente.
Embora não conheçamos o ruído exatamente, assumimos que
ele provenha de um conjunto randômico de valores de média zero.
Portanto, se definirmos o operador
é o ruído
da imagem. Cada imagem é degradada por um ruído diferente.
Embora não conheçamos o ruído exatamente, assumimos que
ele provenha de um conjunto randômico de valores de média zero.
Portanto, se definirmos o operador 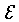 para representar
o valor esperado, isto é, a média
sobre todos os pontos
para representar
o valor esperado, isto é, a média
sobre todos os pontos 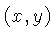 do ruído, podemos escrever:
do ruído, podemos escrever:
![$\displaystyle {\cal{E}}\left[R_i(x,y)\right]=0,$](img169.gif) |
(3.1) |
![$\displaystyle {\cal{E}}\left[R_i(x,y)+R_j(x,y)\right]={\cal{E}}\left[R_i(x,y)\right]+ {\cal{E}}\left[R_j(x,y)\right],$](img170.gif) 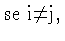 |
(3.2) |
e
![$\displaystyle {\cal{E}}\left[R_i(x,y)\cdot R_j(x,y)\right]={\cal{E}}\left[R_i(x,y)\right] \cdot{\cal{E}}\left[R_j(x,y)\right],$](img172.gif) 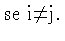 |
(3.3) |
Se obtivermos a média de M imagens:
o quadrado da razão sinal ruído (SNR) será:
O numerador não foi alterado porque o sinal médio é igual ao sinal.
Fatorando o fator 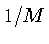 do denominador, obtemos:
Utilizando a propriedade (3.2), podemos separar o
denominador em dois termos:
O primeiro termo pode ser escrito como a soma dos valores esperados,
e o segundo termo pode ser fatorado:
A condição (3.1) implica que o segundo termo é nulo.
Além disto, como todos as medidas de ruído são vêm
da mesma distribuição, elas são idênticas. Portanto:
ou
isto é, a razão sinal ruído aumenta com a raiz
quadrada do número de imagens promediadas.
do denominador, obtemos:
Utilizando a propriedade (3.2), podemos separar o
denominador em dois termos:
O primeiro termo pode ser escrito como a soma dos valores esperados,
e o segundo termo pode ser fatorado:
A condição (3.1) implica que o segundo termo é nulo.
Além disto, como todos as medidas de ruído são vêm
da mesma distribuição, elas são idênticas. Portanto:
ou
isto é, a razão sinal ruído aumenta com a raiz
quadrada do número de imagens promediadas.




Próxima: Filtragem
Volta: Imagens Digitais
Anterior: Registro
©
Modificada em 21 set 1998
![$\displaystyle \bar{I}(x,y) = \frac{1}{M}\sum_{i=1}^M \left[S(x,y) + R_i(x,y)\right],$](img174.gif)
![$\displaystyle \overline{\mbox{SNR}}^2 = \frac{S^2(x,y)}{{\cal{E}}\left\{\left[\frac{1}{M}\sum_{i=1}^M
R_i(x,y)\right]^2\right\}}.$](img175.gif)
![$\displaystyle \overline{\mbox{SNR}}^2 = \frac{M^2 S^2(x,y)}{{\cal{E}}\left[\sum_{i=1}^M \sum_{j=1}^M
R_i(x,y)\cdot R_j(x,y)\right]}.$](img177.gif)
![$\displaystyle \overline{\mbox{SNR}}^2 = \frac{M^2 S^2(x,y)}{{\cal{E}}\left[\sum...
...underbrace{\sum_{i=1}^M \sum_{j=1}^M}_{i\neq j} R_i(x,y)\cdot R_j(x,y)\right]}.$](img178.gif)
![$\displaystyle \overline{\mbox{SNR}}^2 = \frac{M^2 S^2(x,y)}{\sum_{i=1}^M {\cal{...
...neq j}
{\cal{E}}\left[
R_i(x,y)\right]\cdot
{\cal{E}}\left[
R_j(x,y)\right]}.$](img179.gif)
![$\displaystyle \overline{\mbox{SNR}}^2 = \frac{M^2 S^2(x,y)}{M {\cal{E}}\left[R_i^2(x,y)\right]}
=M\,\mbox{SNR}^2,$](img180.gif)