



Próxima: Translação
Volta: Transformadas de Fourier
Anterior: Transformada Bi-dimensionais
Separabilidade
Uma propriedade da transformada de Fourier, que é utilizada para
calcular uma transformada bi-dimensional como uma sucessão de
duas transformadas uni-dimensionais, é a separabilidade:
ou seja,
onde 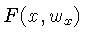 representa a transformada uni-dimensional de
representa a transformada uni-dimensional de 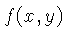 sobre a coordenada
sobre a coordenada 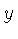 , mantendo-se
, mantendo-se 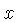 fixo.
fixo.
Da mesma maneira, a transformada inversa também pode ser separada:
Se a função 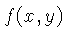 é separável, isto é, pode ser escrita
como
é separável, isto é, pode ser escrita
como
então a transformada também pode ser
separada:
onde
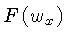 e
e
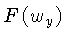 são as transformadas uni-dimensionais de
são as transformadas uni-dimensionais de
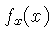 e
e 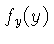 , respectivamente.
, respectivamente.




Próxima: Translação
Volta: Transformadas de Fourier
Anterior: Transformada Bi-dimensionais
©
Modificada em 21 set 1998
![$\displaystyle {\cal{F}}[f(x,y)] \equiv F(w_x,w_y) = \frac{1}{\sqrt{N}}\sum_{x=0...
...\sqrt{M}} \sum_{y=0}^{M-1}
f(x,y) e^{-2i\pi w_yy/M}\right]\,e^{-2i\pi w_xx/N}, $](img250.gif)
![$\displaystyle {\cal{F}}[f(x,y)] \equiv F(w_x,w_y) = \frac{1}{\sqrt{N}}\sum_{x=0...
...\sqrt{M}} \sum_{y=0}^{M-1}
f(x,y) e^{-2i\pi w_yy/M}\right]\,e^{-2i\pi w_xx/N}, $](img250.gif)
![$\displaystyle {\cal{F}}^{-1}[F(w_x,w_y)] \equiv f(x,y) =\frac{1}{\sqrt{N}} \sum...
...{M}}\sum_{w_y=0}^{M-1}
F(w_x,w_y) e^{-2i\pi w_yy/M}\right]\,e^{-2i\pi w_xx/N}. $](img254.gif)
![]() é separável, isto é, pode ser escrita
como
é separável, isto é, pode ser escrita
como