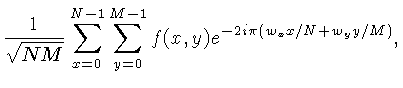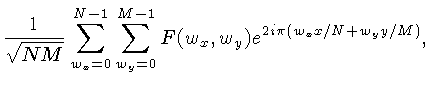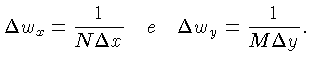Próxima: Separabilidade
Volta: Transformadas de Fourier
Anterior: Transformadas de Fourier
Para funções bi-dimensionais f(x,y):
![$\displaystyle \boxed{{\cal{F}}[f(x,y)] \equiv F(w_x,w_y) = \int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y) e^{-2i\pi (w_xx+w_yy)} dx\,dy,}$](img224.gif) |
(4.6) |
e a transformada inversa:
![$\displaystyle \boxed{{\cal{F}}^{-1}[F(w_x,w_y)] \equiv f(x) =\frac{1}{4\pi^2} \...
...fty}^\infty \int_{-\infty}^\infty F(w_x,w_y) e^{2i\pi (w_xx+w_yy)} dw_x\,dw_y,}$](img225.gif) |
(4.7) |
onde 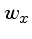 e
e 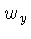 são as freqüências.
são as freqüências.
O espectro de potências
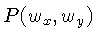 é definido como:
é definido como:
e o ângulo de fase é dado por:
A transformada discreta (DFT) de um sinal é definida como:
![$\displaystyle \boxed{{\cal{F}}[f(x)] \equiv F(w_x) = \frac{1}{\sqrt{N}}\sum_{x=0}^{N-1} f(x) e^{-2i\pi w_xx/N},\quad \mathrm{para\, w_x=0,1,\cdots,N-1}.}$](img231.gif) |
(4.8) |
e a transformada inversa:
![$\displaystyle \boxed{{\cal{F}}^{-1}[F(w_x)] \equiv f(x) = \frac{1}{\sqrt{N}}\sum_{w_x=0}^{N-1} F(w_x) e^{2i\pi w_xx/N},\quad \mathrm{para\, x=0,1,\cdots,N-1}.}$](img232.gif) |
(4.9) |
Os valores da função 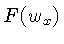 correspondem aos pontos
correspondem aos pontos
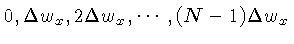 . Assim sendo,
. Assim sendo,
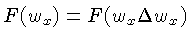 . Para a função
. Para a função 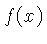 ,
a origem da amostra é o ponto
,
a origem da amostra é o ponto 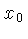 , mas para a transformada
, mas para a transformada
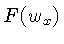 , a origem está sempre em zero, e
, a origem está sempre em zero, e
Esta relação indica que o incremento em freqüência
depende de forma inversa ao número de amostras da função
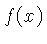 , e do passo usado nesta amostragem. Assim sendo, quando
quisermos conhecer a contribuição de uma determinada
faixa de freqüências na formação de um sinal, precisamos
assegurar-mo-nos que a amostragem do sinal permita que
as freqüências de interesse estejam representadas
(Teorema de amostragem de Nyquist-Shannon).
, e do passo usado nesta amostragem. Assim sendo, quando
quisermos conhecer a contribuição de uma determinada
faixa de freqüências na formação de um sinal, precisamos
assegurar-mo-nos que a amostragem do sinal permita que
as freqüências de interesse estejam representadas
(Teorema de amostragem de Nyquist-Shannon).
Para imagens bi-dimensionais, 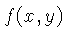 , a transformada é
simplesmente:
, a transformada é
simplesmente:
e a transformada inversa:
Nas figuras a seguir mostramos uma imagem, um círculo e um retângulo,
ao lado de suas transformadas de Fourier.
A relação entre os passos da amostra no domínio
de freqüência e de espaço são dados por:




Próxima: Separabilidade
Volta: Transformadas de Fourier
Anterior: Transformadas de Fourier
©
Modificada em 21 set 1998
![$\displaystyle \boxed{{\cal{F}}[f(x,y)] \equiv F(w_x,w_y) = \int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y) e^{-2i\pi (w_xx+w_yy)} dx\,dy,}$](img224.gif)
![$\displaystyle \boxed{{\cal{F}}[f(x,y)] \equiv F(w_x,w_y) = \int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y) e^{-2i\pi (w_xx+w_yy)} dx\,dy,}$](img224.gif)
![$\displaystyle \boxed{{\cal{F}}^{-1}[F(w_x,w_y)] \equiv f(x) =\frac{1}{4\pi^2} \...
...fty}^\infty \int_{-\infty}^\infty F(w_x,w_y) e^{2i\pi (w_xx+w_yy)} dw_x\,dw_y,}$](img225.gif)
![]() e
e ![]() são as freqüências.
são as freqüências.
![]() é definido como:
é definido como:
![$\displaystyle \phi(w_x,w_x)=\tan^{-1} \frac {\Im[F(w_x,w_x)]}{\Re[F(w_x,w_x)]}.$](img229.gif)

![$\displaystyle \boxed{{\cal{F}}[f(x)] \equiv F(w_x) = \frac{1}{\sqrt{N}}\sum_{x=0}^{N-1} f(x) e^{-2i\pi w_xx/N},\quad \mathrm{para\, w_x=0,1,\cdots,N-1}.}$](img231.gif)
![$\displaystyle \boxed{{\cal{F}}^{-1}[F(w_x)] \equiv f(x) = \frac{1}{\sqrt{N}}\sum_{w_x=0}^{N-1} F(w_x) e^{2i\pi w_xx/N},\quad \mathrm{para\, x=0,1,\cdots,N-1}.}$](img232.gif)
![]() correspondem aos pontos
correspondem aos pontos
![]() . Assim sendo,
. Assim sendo,
![]() . Para a função
. Para a função ![]() ,
a origem da amostra é o ponto
,
a origem da amostra é o ponto ![]() , mas para a transformada
, mas para a transformada
![]() , a origem está sempre em zero, e
, a origem está sempre em zero, e
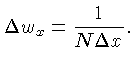
![]() , a transformada é
simplesmente:
, a transformada é
simplesmente: