



Próxima: Periodicidade e Simetria
Volta: Translação
Anterior: Translação em Frequência
A transformada de uma função transladada de 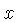 para
para 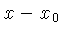 ,
e de
,
e de 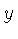 para
para 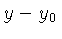 é dada por:
Ou seja, transladando-se a função translada-se também
a transformada, sem afetar sua magnitude:
é dada por:
Ou seja, transladando-se a função translada-se também
a transformada, sem afetar sua magnitude:




Próxima: Periodicidade e Simetria
Volta: Translação
Anterior: Translação em Frequência
©
Modificada em 21 set 1998
![$\displaystyle {\cal{F}}\left[f\left(x-x_0,y-y_0\right)\right] \equiv F\left(w_x...
...0}^{M-1}
f(x,y) e^{-2i\pi (w_xx/N + w_yy/M)}e^{-2i\pi (w_{x0}x/N + w_{y0}y/M)}.$](img275.gif)
![$\displaystyle {\cal{F}}\left[f\left(x-x_0,y-y_0\right)\right] \equiv F\left(w_x...
...0}^{M-1}
f(x,y) e^{-2i\pi (w_xx/N + w_yy/M)}e^{-2i\pi (w_{x0}x/N + w_{y0}y/M)}.$](img275.gif)
