



Próxima: Linearidade
Volta: Transformadas de Fourier
Anterior: Translação em Duas Dimensões
Periodicidade e Simetria
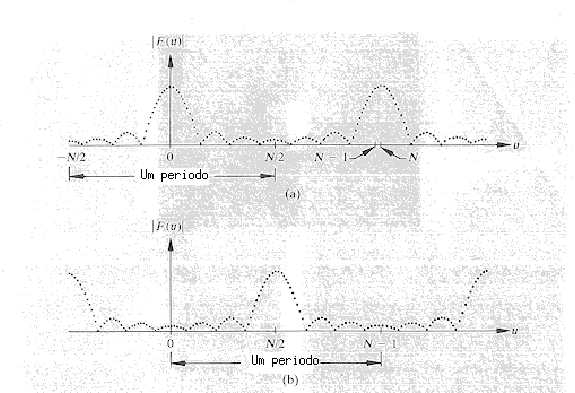
Das equações que definem a transformada, se pode ver
que a transformada de uma função qualquer é uma
função periódica com período N em 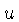 e M em
e M em 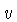 :
Desta propriedade se pode ver que podemos caracterizar uma função
no domínio de frequências completamente, especificando-se
os valores dentro destes períodos, N e M.
Se os sinais f(x,y) forem reais, a transformada é também
simétrica:
:
Desta propriedade se pode ver que podemos caracterizar uma função
no domínio de frequências completamente, especificando-se
os valores dentro destes períodos, N e M.
Se os sinais f(x,y) forem reais, a transformada é também
simétrica:
Se 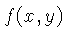 é simétrica, isto é,
é simétrica, isto é,
então a transformada de Fourier também será simétrica:
Se a função 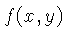 for real, como no caso das imagens,
a transformada de Fourier será uma função imaginária,
com a parte real simétrica, e a parte imaginária anti-simétrica.
Esta propriedade é chamada de propriedade Hermitiana.
for real, como no caso das imagens,
a transformada de Fourier será uma função imaginária,
com a parte real simétrica, e a parte imaginária anti-simétrica.
Esta propriedade é chamada de propriedade Hermitiana.




Próxima: Linearidade
Volta: Transformadas de Fourier
Anterior: Translação em Duas Dimensões
©
Modificada em 21 set 1998
![]() é simétrica, isto é,
é simétrica, isto é,
![]() for real, como no caso das imagens,
a transformada de Fourier será uma função imaginária,
com a parte real simétrica, e a parte imaginária anti-simétrica.
Esta propriedade é chamada de propriedade Hermitiana.
for real, como no caso das imagens,
a transformada de Fourier será uma função imaginária,
com a parte real simétrica, e a parte imaginária anti-simétrica.
Esta propriedade é chamada de propriedade Hermitiana.