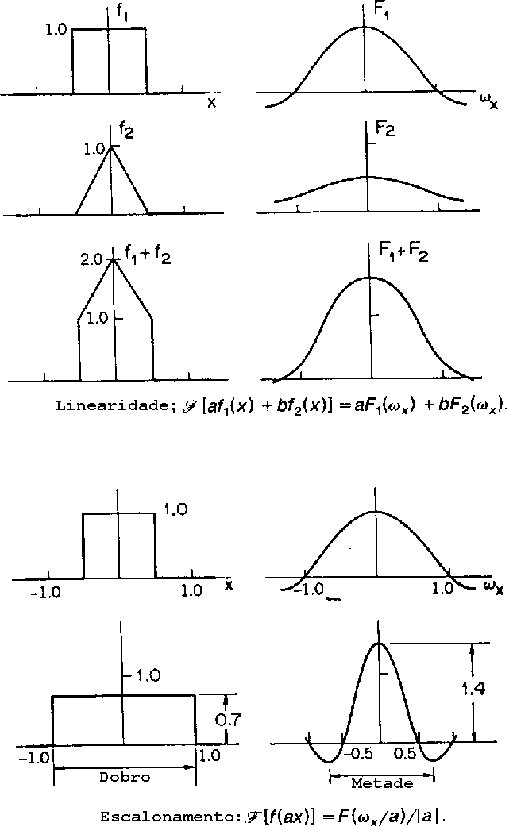Próxima: Teorema da Convolução
Volta: Transformadas de Fourier
Anterior: Linearidade
Escalonamento
Um escalonamento linear nas coordenadas espaciais corresponde a um
escalonamento inverso no domínio de Fourier:
Esta propriedade pode ser facilmente demonstrada fazendo-se
a substituição de variáveis 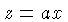 e
e 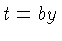 ,
lembrando que
,
lembrando que 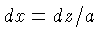 e
e 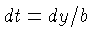 .
Portanto, um aumento do eixo espacial implica em um decréscimo do eixo
correspondente no espaço de Fourier, além de um aumento em amplitude.
.
Portanto, um aumento do eixo espacial implica em um decréscimo do eixo
correspondente no espaço de Fourier, além de um aumento em amplitude.




Próxima: Teorema da Convolução
Volta: Transformadas de Fourier
Anterior: Linearidade
©
Modificada em 21 set 1998
![$\displaystyle {\cal{F}}[f(ax,by)] = \frac{1}{\vert ab\vert}F\left(\frac{w_x}{a},\frac{w_y}{b}\right).$](img288.gif)
![$\displaystyle {\cal{F}}[f(ax,by)] = \frac{1}{\vert ab\vert}F\left(\frac{w_x}{a},\frac{w_y}{b}\right).$](img288.gif)