



Próxima: Teorema de Parseval
Volta: Transformadas de Fourier
Anterior: Escalonamento
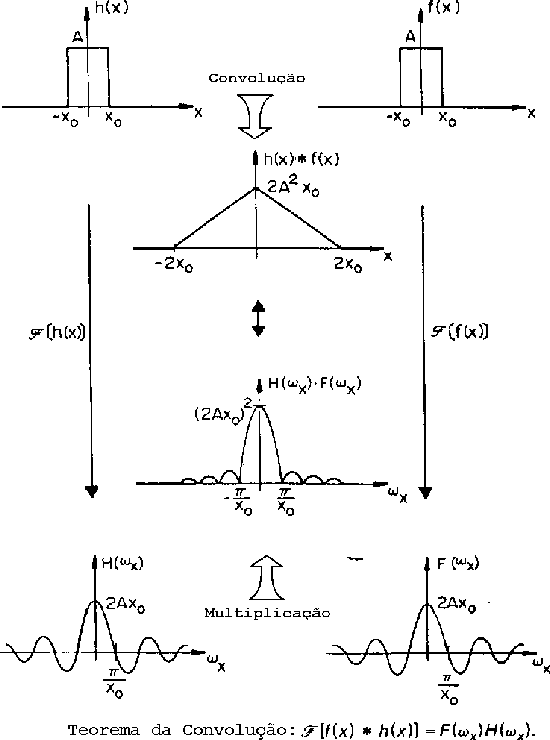
A transformada de Fourier de duas funções convoluídas no
domínio do espaço é igual ao produto das transformadas
das duas funções no domínio de Fourier:
onde o operador 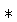 denota a operação de convolução.
Este teorema é de grande importância no processamento de imagens.
denota a operação de convolução.
Este teorema é de grande importância no processamento de imagens.
Consideremos o caso de uma imagem resultante 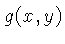 de um sinal
de um sinal 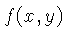 convoluído com uma função de espalhamento
convoluído com uma função de espalhamento 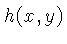 :
:
A transformada de Fourier desta convolução pode ser
obtida revertendo-se a ordem da integração:
Utilizando a propriedade de translação:
obtemos:
Desta maneira utilizamos a propriedade de translação para demonstrar
o teorema da convolução. Como em geral a operação
de convolução é mais complexa de calcular do que a
transformada de Fourier, usa-se este teorema para calcular a
convolução calculando-se a transformada das funções,
sua multiplicação, e a transformada inversa.
O teorema inverso afirma que:




Próxima: Teorema de Parseval
Volta: Transformadas de Fourier
Anterior: Escalonamento
©
Modificada em 21 set 1998
![]() de um sinal
de um sinal ![]() convoluído com uma função de espalhamento
convoluído com uma função de espalhamento ![]() :
:
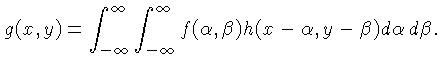
![$\displaystyle {\cal{F}}[g(x,y)] \equiv G\left(w_x,w_y\right) =
\int_{-\infty}^\...
...ta)
e^{\left[-i\left(xw_x+yw_y\right)\right]}dxdy\right\rbrace d\alpha\,d\beta.$](img300.gif)
![$\displaystyle {\cal{F}}\left[h(x-\alpha,y-\beta\right] = H\left(w_x,w_y\right) e^{-i\left(\alpha w_x + \beta w_y\right)},$](img301.gif)
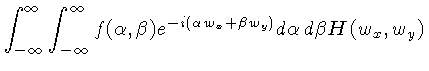
![$\displaystyle {\cal{F}}\left[f(x,y)h(x,y)\right] = \frac{1}{4\pi^2}\left[F(w_x,w_y)*H(w_x,w_y)\right].$](img305.gif)