



Próxima: Gaussiana
Volta: Transformadas de Fourier
Anterior: Transformada de Hankel
Se fizermos uma rotação de coordenadas 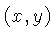 para
para 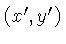 ,
onde:
as coordenadas no domínio de Fourier também sofrem uma rotação:
,
onde:
as coordenadas no domínio de Fourier também sofrem uma rotação:




Próxima: Gaussiana
Volta: Transformadas de Fourier
Anterior: Transformada de Hankel
©
Modificada em 21 set 1998
