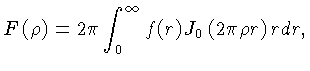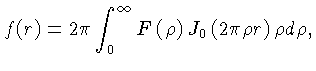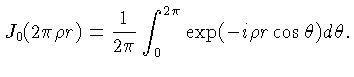Próxima: Rotação
Volta: Transformadas de Fourier
Anterior: Alias
Transformada de Hankel
Muitos sistemas bi-dimensionais possuem simetria esférica, de modo que
as duas coordenadas cartesianas (x,y) podem ser substituídas
por uma variável radial.
onde 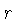 é a coordenada polar:
onde:
A transformada de Fourier equivalente é dada por:
onde
é a coordenada polar:
onde:
A transformada de Fourier equivalente é dada por:
onde 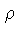 é a frequência espacial, dada por:
onde:
é a frequência espacial, dada por:
onde:
A função
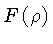 é chamada de transformada de Hankel
da função
é chamada de transformada de Hankel
da função 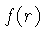 , já que elas estão relacionadas por:
, já que elas estão relacionadas por:
onde 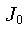 é a função de Bessel de ordem zero:
é a função de Bessel de ordem zero:




Próxima: Rotação
Volta: Transformadas de Fourier
Anterior: Alias
©
Modificada em 21 set 1998

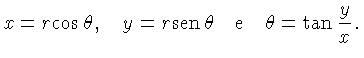
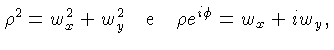
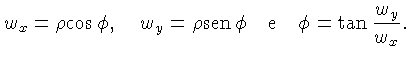
![]() é chamada de transformada de Hankel
da função
é chamada de transformada de Hankel
da função ![]() , já que elas estão relacionadas por:
, já que elas estão relacionadas por: