A Transformada Radon de uma função ![]() ,
representada por
,
representada por
![]() , é definida como a
integral sobre a linha que é paralela ao eixo
, é definida como a
integral sobre a linha que é paralela ao eixo ![]() ,
à uma distância
,
à uma distância ![]() da origem. As coordenadas
da origem. As coordenadas
![]() são as coordenadas obtidas por
rotação das coordenadas
são as coordenadas obtidas por
rotação das coordenadas ![]() por um ângulo
por um ângulo ![]() :
:
Matematicamente, a Transformada Radon, denotada pelo
operador ![]() , é dada por:
, é dada por:
| (4.17) | |||
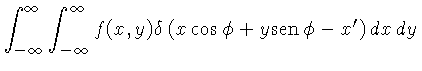 |
(4.18) | ||
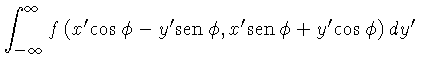 |
(4.19) |
Como a função
![]() é a projeção uni-dimensional
da função
é a projeção uni-dimensional
da função ![]() em um ângulo
em um ângulo ![]() , a transformada
Radon calcula a integral da imagem bi-dimensional sobre o
eixo
, a transformada
Radon calcula a integral da imagem bi-dimensional sobre o
eixo ![]() .
.
Naturalmente a Transformada Radon, ou projeção, é
periódica em ![]() , e é simétrica, com
, e é simétrica, com