Vamos considerar a relação entre a transformada de Fourier
bi-dimensional da função objeto ![]() e a transformada
de Fourier uni-dimensional da projeção
e a transformada
de Fourier uni-dimensional da projeção
![]() .
Esta relação nos dá o Teorema da Projeção ou
Teorema da Faixa Central (Central Slice Theorem),
que é a relação fundamental para a reconstrução
por projeções. A transformada uni-dimensional
da projeção
.
Esta relação nos dá o Teorema da Projeção ou
Teorema da Faixa Central (Central Slice Theorem),
que é a relação fundamental para a reconstrução
por projeções. A transformada uni-dimensional
da projeção
![]() é dada por:
é dada por:
| (4.20) | |||
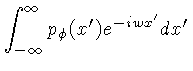 |
(4.21) | ||
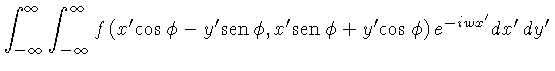 |
(4.22) |
Transformando as coordenadas de ![]() para
para ![]() ,
usando-se as relações acima, podemos reescrever:
,
usando-se as relações acima, podemos reescrever:
![$\displaystyle P_\phi(w) = \int_{-\infty}^\infty \int_{-\infty}^\infty
f(x,y)\exp\left[-iw(x\cos\phi + y\mathrm{sen}\,\phi\right]dx\,dy.$](img417.gif)
| (4.23) | |||
| (4.24) | |||
| (4.25) |
Demonstramos portanto que a transformada de Fourier da projeção
![]() , em um certo ângulo
, em um certo ângulo ![]() , é igual ao
dado radial passando na origem em uma direção
dada pelo ângulo
, é igual ao
dado radial passando na origem em uma direção
dada pelo ângulo ![]() na
transformada de Fourier dos dados. Com esta transformada de
Fourier, podemos calcular a função
na
transformada de Fourier dos dados. Com esta transformada de
Fourier, podemos calcular a função
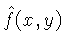 usando-se
a transformada inversa:
usando-se
a transformada inversa: