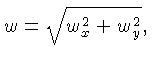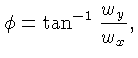Próxima: Reconstrução Bi-dimensional por Retro-projeção Filtrada
Volta: Transformadas de Fourier
Anterior: Teorema da Projeção ou Teorema da
Ao invés de calcular a transformada inversa das projeções
diretamente, a maior parte dos algoritmos calcula
a chamada retro-projeção (filtered backprojection -FB),
que demonstraremos agora:
Se escrevermos
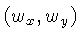 na equação 4.28
em coordenadas polares
na equação 4.28
em coordenadas polares 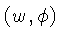 , podemos mostrar que:
, podemos mostrar que:
![$\displaystyle \hat{f}(r,\theta) = \int_{0}^{2\pi} \int_{0}^\infty F(w,\phi)\exp\left[iw(x\cos \phi + y\mathrm{sen}\,\phi)\right]\vert w\vert\,dw\,d\phi,$](img432.gif) |
(4.29) |
onde:
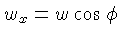 e
e
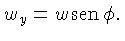 Mudando-se os limites de integração na equação 4.28
para
Mudando-se os limites de integração na equação 4.28
para
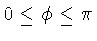 e
e
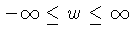 , e
substituindo
, e
substituindo 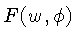 por
por 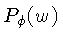 , a equação 4.28
pode ser reescrita como:
, a equação 4.28
pode ser reescrita como:
onde
Na última linha fizemos uso do teorema da convolução;
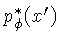 representa a retro-projeção dos dados.
representa a retro-projeção dos dados.




Próxima: Reconstrução Bi-dimensional por Retro-projeção Filtrada
Volta: Transformadas de Fourier
Anterior: Teorema da Projeção ou Teorema da
©
Modificada em 21 set 1998
![]() na equação 4.28
em coordenadas polares
na equação 4.28
em coordenadas polares ![]() , podemos mostrar que:
, podemos mostrar que: