Próxima: Imageamento Fourier em Ressonância Nuclear Magnética
Volta: Transformadas de Fourier
Anterior: Reconstrução Bi-dimensional por Retro-projeção Filtrada
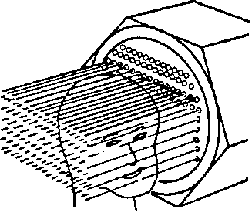
Para a reconstrução dos dados de uma câmara cintiladora
em rotação, definimos:
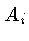 = atividade no voxel i.
= atividade no voxel i.
-
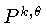 = projeção do raio
= projeção do raio 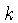 para câmara em
um ângulo
para câmara em
um ângulo 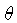 a partir de uma direção
a partir de uma direção 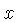 .
.
-
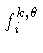 = volume fracional do voxel
= volume fracional do voxel 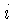 contido
na projeção
contido
na projeção 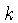 .
.
-
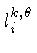 = comprimento da porção
do raio
= comprimento da porção
do raio 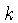 que está contida no voxel
que está contida no voxel 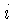 , de modo que
a atenuação sofrida pelo raio
, de modo que
a atenuação sofrida pelo raio 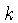 ao atravessar o voxel
ao atravessar o voxel
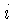 é
é
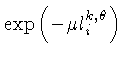 .
.
-
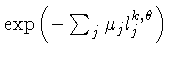 = fator de atenuação
para a radiação proveniente do voxel
= fator de atenuação
para a radiação proveniente do voxel 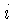 . O índice
. O índice
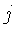 denota elementos no raio
denota elementos no raio 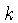 entre o voxel
entre o voxel 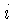 e a
borda do órgão mais próxima do detector.
e a
borda do órgão mais próxima do detector.
A projeção medida por ser expressa por:
A reconstrução pode ser feita pela retro-projeção, mas
as dificuldades específicas do SPECT são: a) variação
da resolução espacial e sensibilidade com a distância
ao colimador, b) falta de um método acurado para
corrigir por atenuação (note que o termo de atenuação
não está presente na reconstrução da tomografia
computadorizada), e c) espalhamento da radiação gama
dentro do corpo.
Devido a resolução finita em energia no detector,
muitos fótons espalhados são indistingüíveis
dos fótons primários, e portanto medidos como sinal.
Como os fótons espalhados se originam principalmente
de fora do voxel de interesse, eles causam borramento
e redução de contraste da imagem. Para corrigir
pela atenuação os algoritmos deveriam ser iterativos,
mas como são muitos lentos, não são utilizados
clinicamente. A atenuação pode, entretanto, ser parcialmente corrigida
usando-se um filtro adicional que leve em conta
a projeção conjugada.




Próxima: Imageamento Fourier em Ressonância Nuclear Magnética
Volta: Transformadas de Fourier
Anterior: Reconstrução Bi-dimensional por Retro-projeção Filtrada
©
Modificada em 21 set 1998

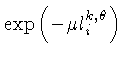 .
.
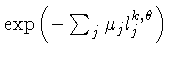 = fator de atenuação
para a radiação proveniente do voxel
= fator de atenuação
para a radiação proveniente do voxel