



Próxima: Reformatação Bi- e Tri-dimensional
Volta: Transformadas de Fourier
Anterior: Imagem SPECT
Imageamento Fourier em Ressonância Nuclear Magnética
Núcleons que contém um número ímpar de prótons,
neutrons, ou ambos, em combinação,
(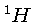 ,
, 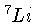 ,
, 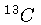 ,
, 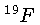 ,
, 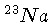 ,
, 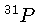 , e
, e  )
possuem momento magnético nuclear.
)
possuem momento magnético nuclear.
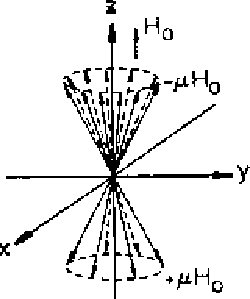
Quando sujeitos a um campo magnético externo, eles giram
e precessionam como piões ao redor da direção
do campo magnético. A frequência de precessão,
ou rotação, é chamada de frequência de precessão
de Larmor, ou simplesmente frequência de Larmor:
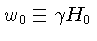 ,
onde
,
onde 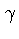 é a razão giromagnética, e
é a razão giromagnética, e 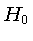 é o fluxo
magnético externo. Ao passar de momento magnético nuclear
paralelo ao campo para antiparalelo, eles absorvem
uma energia
do sinal de radio-frequência externo empregado para mudar
a direção dos spins nucleares.
é o fluxo
magnético externo. Ao passar de momento magnético nuclear
paralelo ao campo para antiparalelo, eles absorvem
uma energia
do sinal de radio-frequência externo empregado para mudar
a direção dos spins nucleares.
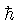 é a contante de Planck.
Após cessar o
sinal de rádio externo, os núcleons
excitados tendem a retornar ao nível
de mais baixa energia, com spins paralelos ao campo externo,
emitindo a mesma frequência absorvida. Este sinal
é medido por uma bobina, e é chamado de
sinal de decaimento de indutância livre (Free Induction
Decay - FID). A razão giromagnética, e portanto a energia,
é única para cada tipo de núcleon.
é a contante de Planck.
Após cessar o
sinal de rádio externo, os núcleons
excitados tendem a retornar ao nível
de mais baixa energia, com spins paralelos ao campo externo,
emitindo a mesma frequência absorvida. Este sinal
é medido por uma bobina, e é chamado de
sinal de decaimento de indutância livre (Free Induction
Decay - FID). A razão giromagnética, e portanto a energia,
é única para cada tipo de núcleon.
Normalmente dois mecanismos de relaxação estão envolvidos:
a relaxação transversa (spin-spin), 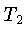 ,
e a relaxação longitudinal (spin-rede),
,
e a relaxação longitudinal (spin-rede), 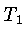 .
.
Por exemplo, para campos de 1 a 20 kG,
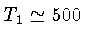 ms,
e
ms,
e
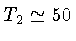 ms. Os valores de
ms. Os valores de 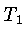 e
e 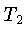 diferem
significativamente para tecido normal e muitos
tecidos malignos, e portanto podem ser utilizados para
diagnosticá-los.
diferem
significativamente para tecido normal e muitos
tecidos malignos, e portanto podem ser utilizados para
diagnosticá-los. 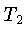 , por interação spin-spin,
leva à perda de fase entre os spins, isto é,
à perda de coerência do sinal, enquanto
, por interação spin-spin,
leva à perda de fase entre os spins, isto é,
à perda de coerência do sinal, enquanto 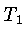 leva ao equilíbrio térmico, realinhando
o spin com o campo externo.
leva ao equilíbrio térmico, realinhando
o spin com o campo externo.
Na ressonância nuclear magnética, o sinal medido
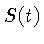 é normalmente conhecido como sinal de eco,
ou decaimento da indutância livre (FID).
Ele mede diretamente a magnetização transversa no volume excitado.
Assumindo que o campo magnético externo está na direção
é normalmente conhecido como sinal de eco,
ou decaimento da indutância livre (FID).
Ele mede diretamente a magnetização transversa no volume excitado.
Assumindo que o campo magnético externo está na direção 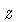 ,
o sinal é dado por:
,
o sinal é dado por:
onde
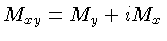 é a magnetização transversa.
O sinal pode ser escrito como:
onde
é a magnetização transversa.
O sinal pode ser escrito como:
onde 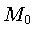 é a magnetização de equilíbrio,
é a magnetização de equilíbrio,
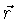 é o vetor posição,
é o vetor posição, 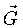 é a forma
de onda do gradiente do campo,
é a forma
de onda do gradiente do campo,
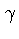 é a razão giromagnética,
e
é a razão giromagnética,
e
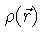 é a densidade de spins.
é a densidade de spins.
Para uma fatia (slice) no plano 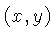 ,
em um posição
,
em um posição 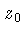 , o sinal
pode ser representado como:
, o sinal
pode ser representado como:
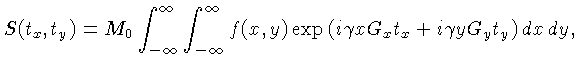 |
(4.50) |
onde 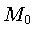 é a magnetização de equilíbrio,
é a magnetização de equilíbrio,
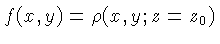 é a distribuição da
densidade bi-dimensional de spins
(por exemplo, da densidade de prótons),
é a distribuição da
densidade bi-dimensional de spins
(por exemplo, da densidade de prótons),
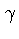 é a razão giro-magnética angular,
é a razão giro-magnética angular,
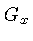 e
e 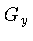 são os gradientes dos campos nas direções
são os gradientes dos campos nas direções
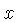 e
e 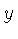 , respectivamente,
impostos deliberadamente para resolver espacialmente
a distribuição de spins,
e
, respectivamente,
impostos deliberadamente para resolver espacialmente
a distribuição de spins,
e 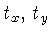 representam a duração do pulso.
Na equação (4.49), se substituirmos
representam a duração do pulso.
Na equação (4.49), se substituirmos
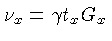 e
e
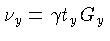 , podemos escrever:
, podemos escrever:
![$\displaystyle S(t_x,t_y) = M_0 \int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y)\exp\left[i\left(w_xt_x+w_yt_y \right)\right] dx\,dy.$](img526.gif) |
(4.51) |
Portanto, o sinal
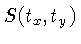 é
a transformada de Fourier da densidade de spins
é
a transformada de Fourier da densidade de spins 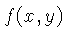 .
A densidade de spins
.
A densidade de spins 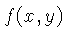 pode portanto ser reconstruída
simplesmente tomando-se a transformada inversa do sinal
pode portanto ser reconstruída
simplesmente tomando-se a transformada inversa do sinal
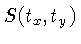 .
Variando-se os gradientes
.
Variando-se os gradientes 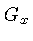 e
e 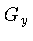 , podemos obter os dados
no domínio cartesiano sem qualquer interpolação.
, podemos obter os dados
no domínio cartesiano sem qualquer interpolação.
O algoritmo específico a ser utilizado na
reconstrução da ressonância nuclear magnética
depende diretamente da sequência de pulsos utilizada.
Para o imageamento de órgãos em movimento, como coração
e abdôme, o imageamento deve ser sincronizado com o movimento
fisiológico para evitar borramento e a introdução
de artefatos, e que pode ser feito utilizando um
eletrocardiograma ou monitoramento dos sinais respiratórios.




Próxima: Reformatação Bi- e Tri-dimensional
Volta: Transformadas de Fourier
Anterior: Imagem SPECT
©
Modificada em 21 set 1998
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , e
, e ![]() )
possuem momento magnético nuclear.
)
possuem momento magnético nuclear.
![]() ,
e a relaxação longitudinal (spin-rede),
,
e a relaxação longitudinal (spin-rede), ![]() .
.
![]() é normalmente conhecido como sinal de eco,
ou decaimento da indutância livre (FID).
Ele mede diretamente a magnetização transversa no volume excitado.
Assumindo que o campo magnético externo está na direção
é normalmente conhecido como sinal de eco,
ou decaimento da indutância livre (FID).
Ele mede diretamente a magnetização transversa no volume excitado.
Assumindo que o campo magnético externo está na direção ![]() ,
o sinal é dado por:
,
o sinal é dado por:
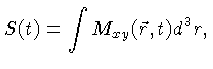
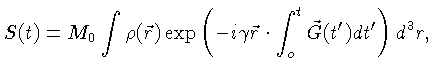
![]() ,
em um posição
,
em um posição ![]() , o sinal
pode ser representado como:
, o sinal
pode ser representado como: