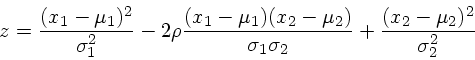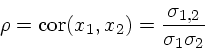Mínimos Quadrados
Em 1809, Carl Friedrich Gauss (1777-1855) publicou um artigo no
Werke, 4, 1-93,
demonstrando que a melhor maneira de determinar
um parâmetro desconhecido de uma equação
de condições é minimizando a soma dos quadrados dos
resíduos, mais tarde chamado de Mínimos Quadrados por
Adrien-Marie Legendre (1752-1833).
Em abril de 1810, Pierre-Simon Laplace (1749-1827) apresenta no
memoir da Academia de Paris,
["Mémoire
sur les approximations des formules qui sont fonctions de très-grands nombres, et sur leur application aux probabilités (suite)".
Mémoires l'Institut 1809 (1810), 353-415, 559-565. Oeuvres 12 p.301-345, p.349-353]
a generalização a problemas com
vários parâmetros desconhecidos.
Um programa de mínimos quadrados sempre começa com a minimização da soma:
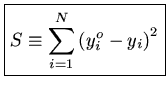 |
(1) |
onde chamamos de
yoi = valores observados de y
yi = valores calculados de y
ou seja, mínimos quadrados implica em minimizar os quadrados dos
resíduos. Estes resíduos podem ser normalizados pelo número de
pontos ou pela soma dos pesos empregados.
Por que este critério é considerado um bom critério e não simplismente
minimizar os resíduos ou o cubo dos resíduos? A resposta formal é que
os mínimos quadrados são corretos se os resíduos tiverem uma distribuição
gaussiana (normal).
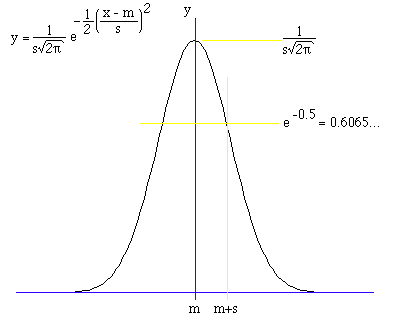
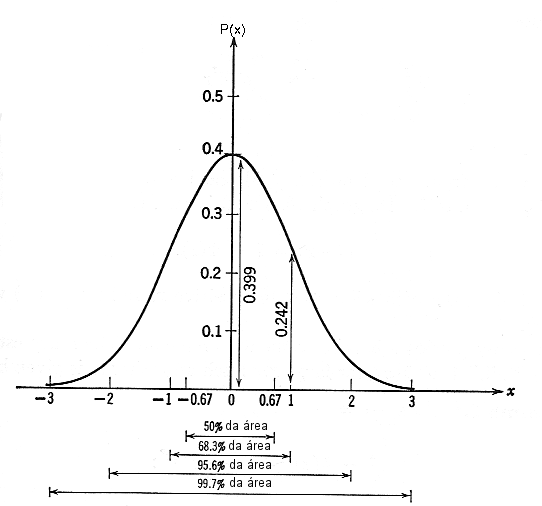
Distribuição gaussiana (normal) para uma variável x, com média m e desvio padrão s.
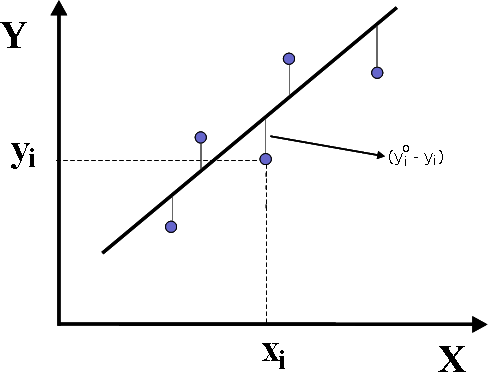
É simples notar que se minimizarmos os resíduos
diretamente, um grande resíduo negativo pode ser anulado por um grande
resíduo positivo, enquanto que com o quadrado minimizamos os módulos
das diferenças.
Suponhamos que temos um conjunto de dados y com uma distribuição normal:
onde
| P(y) |
= |
probabilidade de obter o valor y |
|
| y |
= |
quantidade a ser observada |
|
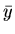 |
= |
valor médio de y |
|
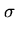
|
= |
desvio padrão de y |
|
Por exemplo,
a probabilidade de se encontrar uma medida entre
-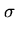 e +
e +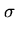 é de 68,3%,
é de 68,3%,
a probabilidade de se encontrar uma medida entre
-1,5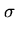 e
+1,5
e
+1,5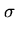 é de 86,6%,
é de 86,6%,
a probabilidade de se encontrar uma medida entre
-2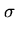 e +2
e +2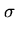 é de 95,4%,
é de 95,4%,
a probabilidade de se encontrar uma medida entre
-2,5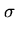 e
+2,5
e
+2,5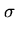 é de 98,76%,
é de 98,76%,
a probabilidade de se encontrar uma medida entre
-3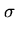 e
+3
e
+3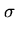 é de 99,74%.
é de 99,74%.
Suponhamos que medimos o valor de y várias vezes, obtendo uma série de
valores {yi}.
A probabilidade de observar este conjunto é dada por
P y1, y2, y3,..., yN y1, y2, y3,..., yN |
= |
![$ \{{\frac{1}{\sigma \sqrt{2\pi}}\exp [-\frac{1}{2\sigma^2}
(y_1-\bar{y})^2]}.$](img14.png) 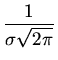 exp exp - - 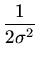 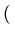 y1 - y1 - 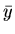 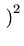 ![$ .{-\frac{1}{2\sigma^2}
(y_1-\bar{y})^2}]$](img18.png) ![$ .{\frac{1}{\sigma \sqrt{2\pi}}\exp [-\frac{1}{2\sigma^2}
(y_1-\bar{y})^2]}\}$](img19.png) ![$ \{{\frac{1}{\sigma \sqrt{2\pi}}\exp [-\frac{1}{2\sigma^2}
(y_2-\bar{y})^2]}.$](img20.png) 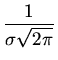 exp exp - - 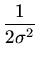  y2 - y2 - 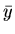 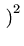 ![$ {-\frac{1}{2\sigma^2}
(y_2-\bar{y})^2}]$](img24.png) ![$ {\frac{1}{\sigma \sqrt{2\pi}}\exp [-\frac{1}{2\sigma^2}
(y_2-\bar{y})^2]}\}$](img25.png) ... ... |
|
| |
|
...![$ \{{\frac{1}{\sigma \sqrt{2\pi}}\exp [-\frac{1}{2\sigma^2}
(y_N-\bar{y})^2]}.$](img26.png) 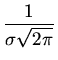 exp exp - - 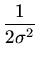  yN - yN - 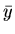  ![$ .{-\frac{1}{2\sigma^2}
(y_N-\bar{y})^2}]$](img30.png) ![$ {\frac{1}{\sigma \sqrt{2\pi}}\exp [-\frac{1}{2\sigma^2}
(y_N-\bar{y})^2]}\}$](img31.png) |
|
| |
= |
 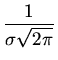 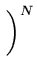 exp exp - - 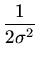 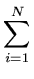 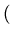 yi - yi - 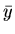 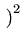 ![$ .{-\frac{1}{2\sigma^2}
\sum_{i=1}^N (y_i-\bar{y})^2}]$](img38.png) |
|
Queremos agora saber qual é o melhor valor de 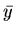 , o valor médio.
O melhor valor será aquele que maximiza a probabilidade de obter os
valores observados {yi}, ou seja, o melhor valor de
, o valor médio.
O melhor valor será aquele que maximiza a probabilidade de obter os
valores observados {yi}, ou seja, o melhor valor de 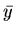 é
obtido colocando a derivada da probabilidade como nula:
Ou seja
Como o termo
exp[...] não pode ser nulo, obtemos
ou na nossa notação
Continuando com a derivação, obtemos:
é
obtido colocando a derivada da probabilidade como nula:
Ou seja
Como o termo
exp[...] não pode ser nulo, obtemos
ou na nossa notação
Continuando com a derivação, obtemos:
| 0 |
= |
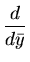 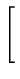 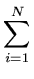 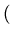 yi - yi - 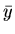 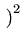 ![$ .{\sum_{i=1}^N (y_i-\bar{y})^2}]$](img46.png) |
|
| |
= |
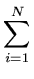 - 2 - 2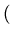 yi - yi - 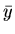 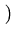 |
|
| |
= |
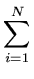 yi - yi - 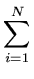 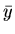 |
|
N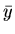
=
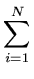 yi
yi
que é a média simples, como queríamos.
O próximo passo é simplesmente reconhecer que y pode ser uma função,
por exemplo:
yi = a + b xi
de modo que
Minimizando S em relação a a e b, obtemos:
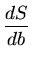
=
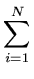
- 2
xio yoi
yoi -
a -
b xoi
= 0
ou as duas condições:
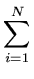 yio
yio -
Na -
b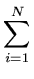 xio
xio = 0
Em notação matricial podemos escrever as duas condições como:
Para simplificar a notação, vamos definir os colchetes:
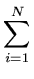 xi
xi 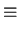
[
x]
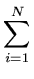
1 =
N 
[1]
desta forma, nossa equação matricial se escreve como:
Estas equações são chamadas de equações normais. Elas podem ser resolvidas com
a matriz inversa:
Para sabermos se, quando passamos de uma fitagem de uma reta para uma fitagem
de uma parábola, a redução no resíduo, com qualquer normalização,
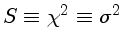 é
suficiente para que
o termo quadrático seja significativo, podemos definir um parâmetro
e determinar o nível de confiabilidade que podemos descartar a
hipótese do termo quadrático ser nulo por
onde
a distribuição da variável F
[Sir Ronald Aylmer Fisher (1890-1962) 1925,
Statistical
Methods for Research Workers. Oliver and Boyd (Edinburgh)]
precisa ser calculada com
F(a,b) é a variável x da função beta incompleta betai(x,df1,df2),
a probabilidade de que uma variável randômica
de uma distribuição beta de graus de liberdade df1 e df2 terá valor menor ou igual a x
[Statistical Theory and Methodology in Science and Engineering.
K. A. Brownlee. London and New York: John Wiley and Sons. 1960].
é
suficiente para que
o termo quadrático seja significativo, podemos definir um parâmetro
e determinar o nível de confiabilidade que podemos descartar a
hipótese do termo quadrático ser nulo por
onde
a distribuição da variável F
[Sir Ronald Aylmer Fisher (1890-1962) 1925,
Statistical
Methods for Research Workers. Oliver and Boyd (Edinburgh)]
precisa ser calculada com
F(a,b) é a variável x da função beta incompleta betai(x,df1,df2),
a probabilidade de que uma variável randômica
de uma distribuição beta de graus de liberdade df1 e df2 terá valor menor ou igual a x
[Statistical Theory and Methodology in Science and Engineering.
K. A. Brownlee. London and New York: John Wiley and Sons. 1960].
exemplos de χ2].
Pelo teorema do limite central, se o número de graus de liberdade for grande (maior que 30),
a distribuição de χ2 tende à distribuição normal, f=σ12/σ22.
Atente que a definição acima é Fp[(df1-df2),df2], e não F(df1,df2) como usado em geral. Aqui se
usou Fp(1,n-3), ou seja df1-df2=1, a diferença no número de graus de liberdade quando passamos de reta para parábola.
A definição geral, usada para calcular a probabilidade é
F = [σ21/σ22 * (N-k1)/(N-k2) - 1] * (N-k2)
Outra maneira de analisar a significância do número de parâmetros ajustados é notar que pela definição da distribuição de probabilidades de χ2, o valor esperado de
χ2 com k graus de liberdade deve estar no intervalo
⟨χ2⟩±σχ2=k±√(2k)
e k=n-m-1, onde n é o número de observações, m o número de parâmetros ajustados, de modo que
χ2=∑in wi[yi-f(xi,a0,...,am)]2/σi
tem que estar neste intervalo. Se for menor, o número de parâmetros está superestimado.
Os mínimos quadrados são lineares quando podemos resolver as equações normais
usando álgebra linear. O exemplo dado acima é um mínimo quadrado linear, pois
podemos resolver as equações para a e b exatamente.
Muitos problemas interessantes não podem ser resolvidos linearmente.
Por exemplo, qual é o melhor valor de 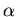 em
em
y = exp(-
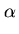 x
x)
Pela nossa definição de S:
e quando minimizamos S:
ou seja
0 =
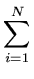 yioxi
yioxiexp
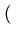
-
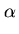 xi
xi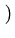
-
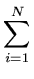 xi
xiexp
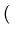
-2
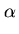 xi
xi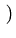
Precisamos utilizar técnicas diferentes. A técnica mais empregada e, de fato,
a técnica que se utiliza quando chamamos de mínimos quadrados
não lineares, é a linearização do problema.
A idéia, aplicada ao problema acima, é:
y = exp(-
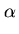 x
x)
Escolhemos um valor inicial de 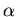 , chamado
, chamado 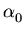 , e definimos:
Definindo
, e definimos:
Definindo
y0 = exp(-
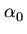 x
x)
Em primeira ordem, isto é, linear:
Agora y é linear em

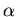 e podemos usar os mínimos quadrados
lineares para encontrar a correção
e podemos usar os mínimos quadrados
lineares para encontrar a correção

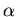 :
que se torna
que minimizando
ou, na notação dos colchetes:
Que podemos resolver para
:
que se torna
que minimizando
ou, na notação dos colchetes:
Que podemos resolver para

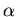 :
e finalmente obter o valor revisado de
:
e finalmente obter o valor revisado de 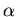 :
Note entretanto que o valor revisado de
:
Note entretanto que o valor revisado de 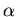 não é o melhor
valor de
não é o melhor
valor de 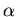 , mas somente uma melhor aproximação do que
, mas somente uma melhor aproximação do que
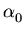 . Isto ocorre porque
. Isto ocorre porque

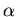 é a solução
do problema linearizado e não do problema real. Portanto,
precisamos iterar, isto é, utilizar este valor revisado de
é a solução
do problema linearizado e não do problema real. Portanto,
precisamos iterar, isto é, utilizar este valor revisado de
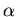 como um novo
como um novo 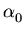 e obter um novo valor revisado.
e obter um novo valor revisado.
Se a função y for uma função de k parâmetros que queremos ajustar:
yi =
y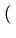 xi
xi,
a1,
a2,...,
ak
colocamos
com a hipótese de que
 ai
ai  ai, 0.
ai, 0.
Então podemos linearizar
| yi |
= |
y xi, a1, 0, a2, 0,..., ak, 0 xi, a1, 0, a2, 0,..., ak, 0 + + 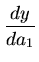 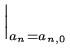  a1 + a1 + 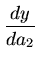 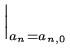 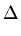 a2 + ... a2 + ... |
|
| |
|
+ ... + 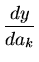 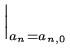 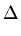 ak ak |
|
notando que as derivadas são calculadas para todos
an = an, 0.
Chamando
yi, 0 =
y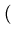 xi
xi,
a1, 0,
a2, 0,...,
ak, 0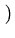
e
podemos escrever
onde o subscrito i significa calculado no ponto xi.
Podemos agora calcular S:
que minimizando com respeito a
 am:
que na notação dos colchetes pode ser escrita como:
Ou, em notação matricial
Esta equação matricial pode agora ser revolvida por álgebra matricial
para encontrar as correções
am:
que na notação dos colchetes pode ser escrita como:
Ou, em notação matricial
Esta equação matricial pode agora ser revolvida por álgebra matricial
para encontrar as correções
 am.
am.
No caso linear
Somente um valor com sua incerteza permite reconstruir a distribuição
de probabilidades de um parâmetro.
A maneira correta de determinar as incertezas nos parâmetros é calculando
a variança de um parâmetro qualquer z:
onde o quadrado é necessário pelas mesmas considerações do valor de S,
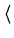 a
a
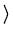 significa a média e onde
significa a média e onde
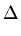 z
z =
zcalculado -
zobservado
Agora suponhamos que z seja uma função de duas variáveis x e y,
z = z(x, y).
Podemos expandir por série de Taylor [Brook Taylor (1685-1731),
Methodus incrementorum directa et inversa (1715)]:
de onde obtemos:
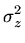 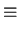 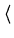 ( (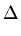 z)2 z)2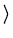 |
= |
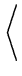 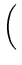 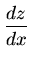  x + x + 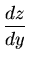 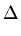 y y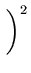  |
|
| |
= |
 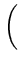 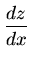 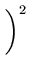 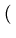 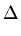 x x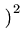 + 2 + 2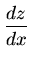 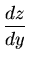 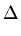 x x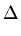 y + y + 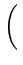 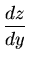 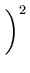 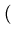 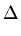 y y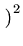 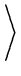 |
|
Se as variáveis x e
y são
separáveis, podemos reduzir
a equação acima a
e, por definição:
de modo que
E como obtemos 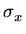 ,
, 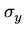 e
e
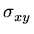 ? Definindo
a matriz covariança.
? Definindo
a matriz covariança.
Definimos a matriz covariança como
De modo que, se a equação normal matricial
que usamos para achar os coeficientes é escrita como
de modo que a solução é dada por
onde
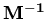 é a matriz inversa da matriz
é a matriz inversa da matriz 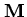 ,
vemos que a matriz covariança é dada por
onde
Desta maneira é muito fácil calcular as incertezas nos parâmetros, pois
somente precisamos multiplar a matriz inversa que usamos para obter os
valores dos parâmetros, por
,
vemos que a matriz covariança é dada por
onde
Desta maneira é muito fácil calcular as incertezas nos parâmetros, pois
somente precisamos multiplar a matriz inversa que usamos para obter os
valores dos parâmetros, por 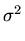 , obtendo a matriz covariança.
Mas o que fazemos se a função a ser fitada não é analítica, como por
exemplo, um espectro resultante de um modelo de atmosferas?
Er-Ho Zhang, Edward L. Robinson e R. Edward Nather (1986,
Astrophysical Journal,
305, 740) demonstraram que no caso
medirmos vários parâmetros simultaneamente, onde a mudança de alguns
pode gerar mudanças significativas, enquanto que a mudança de outros
parâmetros gera pequenas diferenças e, ainda, que os parâmetros não
são independentes, isto é, estão correlacionados, precisamos
maximizar a probabilidade
(likelihood) de que os parâmetros
x1,..., xk sejam medidos
pelos valores
x1o,..., xko, definindo incertezas
, obtendo a matriz covariança.
Mas o que fazemos se a função a ser fitada não é analítica, como por
exemplo, um espectro resultante de um modelo de atmosferas?
Er-Ho Zhang, Edward L. Robinson e R. Edward Nather (1986,
Astrophysical Journal,
305, 740) demonstraram que no caso
medirmos vários parâmetros simultaneamente, onde a mudança de alguns
pode gerar mudanças significativas, enquanto que a mudança de outros
parâmetros gera pequenas diferenças e, ainda, que os parâmetros não
são independentes, isto é, estão correlacionados, precisamos
maximizar a probabilidade
(likelihood) de que os parâmetros
x1,..., xk sejam medidos
pelos valores
x1o,..., xko, definindo incertezas
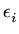 = xio - xi,
= xio - xi,
f (
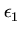
,...,
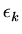
) =
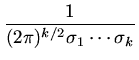
exp
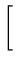
-
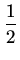
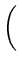
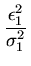
+
... +
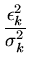
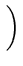
![$ .{-\frac{1}{2}(\frac{\epsilon_1^2}{\sigma_1^2}
+\cdots + \frac{\epsilon_k^2}{\sigma_k^2})}]$](img218.png)
e, portanto, maximizarmos a probabilidade é equivalente a minimizarmos
Note que o valor de 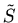 tem normalização diferente da
de S definido na equação
(1). A normalização diferente é que distingue χ2 de S2.
tem normalização diferente da
de S definido na equação
(1). A normalização diferente é que distingue χ2 de S2.
Se medimos os valores Ioi, por exemplo, o espectro, e calculamos
Ii com os parâmetros
x1,..., xk, assumindo que
a distribuição de erros é normal e que todas as varianças são iguais
(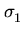 =
= 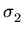 = ... =
= ... = 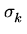 = W), obtemos
= W), obtemos
de modo que, se
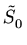 é o valor mínimo de
é o valor mínimo de 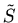 , e se
mudarmos o valor do parâmetro i por um delta d, mantendo todos
os outros parâmetros constantes, obteremos um novo valor de
, e se
mudarmos o valor do parâmetro i por um delta d, mantendo todos
os outros parâmetros constantes, obteremos um novo valor de 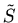 e, portanto,
Portanto podemos obter a incerteza em cada parâmetro minimizando
e, portanto,
Portanto podemos obter a incerteza em cada parâmetro minimizando
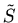 com todos os parâmetros livres, para obter
com todos os parâmetros livres, para obter
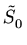 ,
fixando o valor do parâmetro xi para o valor que minimizou
,
fixando o valor do parâmetro xi para o valor que minimizou
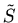 mais um delta, digamos 5%, e minimizando novamente
mais um delta, digamos 5%, e minimizando novamente 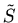 com este valor de xi fixo, obtendo um novo
com este valor de xi fixo, obtendo um novo 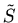 .
Com a equação (2) podemos então estimar o valor de sua incerteza,
e repetir o processo para os outros parâmetros.
.
Com a equação (2) podemos então estimar o valor de sua incerteza,
e repetir o processo para os outros parâmetros.
Podemos encontrar o termo de correlação usando uma transformação de
variáveis
com
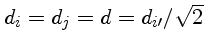 .
Pela propagação de erros,
de modo que
Se a normalização não for unitária, devemos usar:
.
Pela propagação de erros,
de modo que
Se a normalização não for unitária, devemos usar:
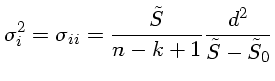 |
(1) |
onde n é o número de pontos, k o número de parâmetros fitados,
e o +1 é porque um dos parâmetros foi mantido fixo, reduzindo o
número de graus de liberdade.
Como demonstrado por
Edward Lewis Robinson (1945-), no seu livro de 2016,
Data Analysis for Scientists and Engineers,
Princeton University Press,
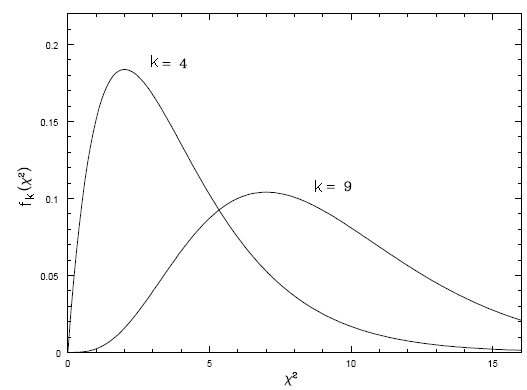
a distribuição de probabilidades de χ2
para k graus de liberdade é dada por
Note que o valor médio de χ2
para k graus de liberdade é k,
a moda é k-2, e a variança σ2χ2=2k.
Algumas vezes se
usa um
χ2
reduzido de modo que sua média seja 1:
Embora o valor médio do χ2red seja 1, a variança continua dependente do número de
graus de liberdade k
⟨χ2red⟩=1
σ2χ2red=2/k
Sabemos que o teorema do limite central garante que a distribuição
de χ2
para k graus de liberdade se aproxima da distribuição
gaussiana para grandes valores de k. Esta aproximação é boa para k>30.
O grande problema do método
χ2
é que ele assume que
as incertezas das medidas são bem determinadas e não correlacionadas.
Se as incertezas forem subestimadas, o valor de χ2 não tem significado.
Estimativa Robusta
O grande problema do método de mínimos quadrados é a grande influência de pontos com resíduo muito grande, os outliers. Para
se reduzir a influência destes resíduos muito grandes, pode-se
minimizar funções que não crescem tão rapidamente quanto
S2, como por exemplo,
mimizando a função discrepância,
definida como:
onde c é uma constante.
A função normal,
centrada em x=0 e com largura em 1/e em
x=1 e x=-1, é definida como
e sua integral é a distribuição normal
Com esta definição
Se tivermos uma distribuição centrada em 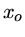 , e de largura
, e de largura 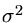 ,
,
O valor da integral de x até infinito, centrada em 0 e com
desvio padrão 1, é
| x=0 | P(>x)=0,5 |
| x=2 | P(>x)=0,02275 |
| x=3 | P(>x)=0,00135 |
| x=4 | P(>x)=0,00003167 |
| x=5 | P(>x)=2,867 × 10-7 |
| x=6 | P(>x)=9,866 × 10-10 |
| x=7 | P(>x)=1,280 × 10-12 |
| x=8 | P(>x)=6,221 × 10-16 |
| x=9 | P(>x)=1,129 × 10-19 |
Se a distribuição é discreta, com N valores:
de modo que precisamos normalizar nossas probabilidades
Distribuição Binominal
Seja um problema que só admite duas soluções, como ao
jogarmos uma moeda.
Chamemos de b(k;n,p) a probabilidade que n tentativas com
probabilidade intrínseca de sucesso p, e q=1-p a
probabilidade intrínseca de insucesso, resulte em k
sucessos e n-k insucessos. Esta probabilidade é dada
pela distribuição binominal
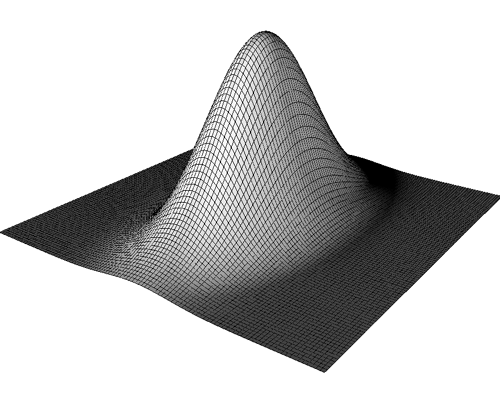
Distribuição gaussiana (normal) para duas variáveis não correlacionadas.
Para duas variáveis correlacionadas, x1 medida a partir
de μ1 e x2 medida a partir
de μ2:
onde
Data analysis recipes: Fitting a model to data, David W. Hogg, Jo Bovy (NYU), Dustin Lang, 2010. arXiv:1008.4686
Tutorial sobre diferentes métodos de ajuste linear a dados, com os problemas de excluir outliers modificando a probabilidade, explicitando que o método
de mínimos quadrados exclui incertezas na variável
de medida (x), isto é
as incertezas são somente em uma dimensão, e assume que as incertezas são todas gaussianas. Inclui exercícios
e uma introdução à estatítica Baesiana. Fornece uma visão crítica sobre os métodos comumente adotados.
É interessante por exemplo a crítica dos autores à metodologia usada para derivar a relação de Tully-Fisher, e a crítica ao uso de PCA (principal component analysis), em ambos casos por terem incertezas nas duas dimensões.
Error estimation in astronomy: A guide. Rene Andrae. 2010. arXiv:1009.2755
Tutorial sobre estimativa das incertezas em parâmetros.
Dos and don'ts of reduced chi-squared (χ2), Rene Andrae, Tim Schulze-Hartung, Peter Melchior, arXiv:1012.3754.
No Excel,
mínimos quadrados lineares são fitados em Tools-Data Analysis-Regression.
Se este pacote não estiver instalado, ele pode ser adicionado com
Tools-Add Ins-Analysis Tool Pack e Solver.
O OpenOffice Calc também pode ser usado.
Com uma subrotina em Fortran de inversão de matrizes, se pode facilmente implementar um algoritmo de
mínimos quadrados.
Maiores detalhes e todas as derivações estão no livro
Data Analysis for Scientists and Engineers, de Edward L. Robinson, 2016, Princeton University Press.
Statistical Calculations
Handbook of Bio Statistics
Fitando períodos com Lorentzianas - Keaton
Relação entre amplitude média e sigma em uma transformada de Fourier
©
Kepler de Souza Oliveira Filho
Modificada em 20 maio 2021
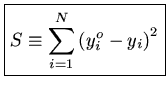
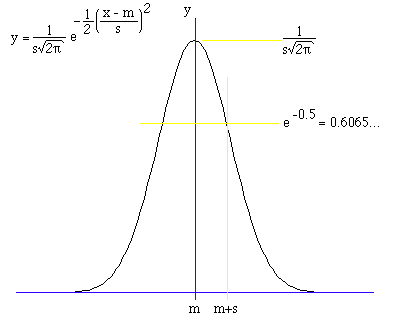
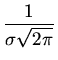 exp
exp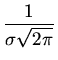 exp
exp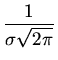 exp
exp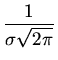 exp
exp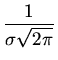
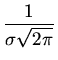
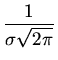
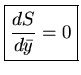
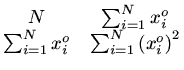
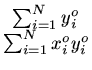
![$ \begin{matrix}[1]&[x]\cr [x]&[x^2]\end{matrix}$](img68.png)
![$\left(\begin{matrix}a\cr b\end{matrix}\right)=
\left(\begin{matrix}[1]&[x]\cr [x]&[x^2]\end{matrix}\right)^{-1}
\left(\begin{matrix}[y]\cr [xy]\end{matrix}\right)$](inv.png)
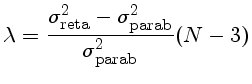
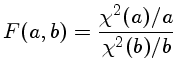
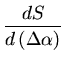 =
= ![$ {\frac{{[y^o \frac{dy}{d\alpha}]
-[y_0 \frac{dy}{d\alpha}]}}{{[(\frac{dy}{d\alpha})^2]}}}$](img124.png)
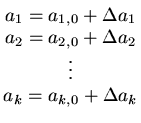
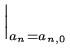
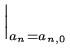
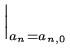
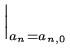
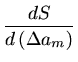 =
= ![$ \begin{matrix}
[\frac{dy}{da_1}\frac{dy}{da_1}]&
...
...dy}{da_2}]&\cdots
[\frac{dy}{da_k}\frac{dy}{da_k}]\end{matrix}$](img160.png)
![$ \begin{matrix}
[(y^o - y_0)\frac{dy}{da_1}]...
...\\
\vdots\\
[(y^o - y_0)\frac{dy}{da_k}]
\end{matrix}$](img166.png)
![$\left(\begin{matrix}
\left[\frac{dy}{da_1}\frac{dy}{da_1}\right] ...\\
\left[\left(y^o - y_0\right)\frac{dy}{da_k}\right]
\end{matrix}\right)$](linear.png)
![]() ,
, ![]() e
e
![]() ? Definindo
a matriz covariança.
? Definindo
a matriz covariança.
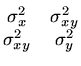
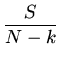 =
= 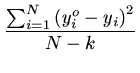
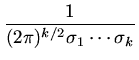 exp
exp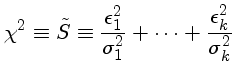
![]() =
= ![]() = ... =
= ... = ![]() = W), obtemos
= W), obtemos
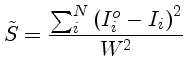
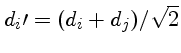
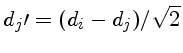
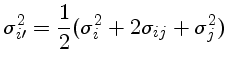
![$f_k(\chi^2) = \frac{(\chi^2)^{(k-2)/2}}{2^{k/2}(k/2-1)!}
\exp{[-\frac{1}{2}\chi^2]}$](fchi.png)
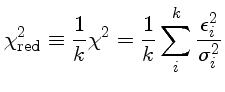
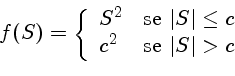
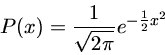
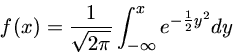
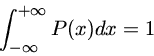
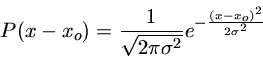
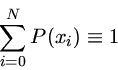
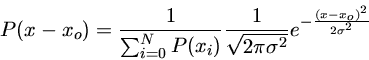
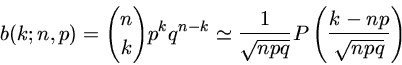

![P(x_1,x_2)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{(1-\rho^2)}}\exp{[-\frac{z}{2(1-\rho^2)}]}](pxy1.gif)