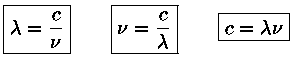
| Fluxo | Magnitude | Extinção |
Fotometria é a medida da luz proveniente de um objeto. Todo o espectro electromagnético, desde a radiação gama até as ondas de rádio são atualmente usadas para observações astronômicas.
Apesar de que observações com satélites, balões e espaçonaves podem ser feitas fora da atmosfera, a grande maioria das observações é obtida da superfície da Terra.
Como a maioria das observações utiliza radiação electromagnética, e podemos obter informações sobre a natureza física da fonte estudando a distribuição de energia desta radiação, explicitamos alguns conceitos para a caracterização desta radiação.
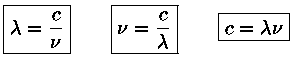
Localização no espectro:
A radiação visível vai aproximadamente de 3900 Å (violeta) até cerca 7800 Å (vermelho).
| Cor | Comprimento de onda (Å) | Freqüência (1012 Hz) |
|---|---|---|
| violeta | 3900 - 4550 | 659 - 769 |
| azul | 4550 - 4920 | 610 - 659 |
| verde | 4920 - 5770 | 520 - 610 |
| amarelo | 5770 - 5970 | 503 - 520 |
| laranja | 5970 - 6220 | 482 - 503 |
| vermelho | 6220 - 7800 | 384 - 482 |
A grandeza mais característica de um campo de radiação é uma constante chamada intensidade específica monocromática. Para melhor entender esse conceito, vamos antes revisar o conceito de ângulo sólido.
Assim como podemos entender um ângulo plano como um setor de um círculo, definido como a razão entre o arco e o raio do círculo, podemos entender um ângulo sólido como um "setor" de uma esfera, definido pela razão entre o elemento de área na superfície da esfera e o seu raio ao quadrado:
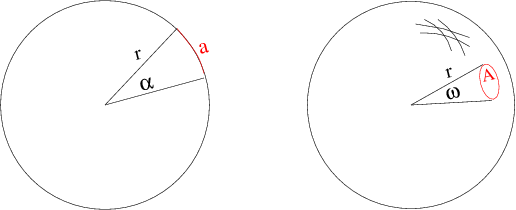

O maior ângulo plano é aquele que subtende toda a circunferência do
círculo, e vale 2![]() radianos; o maior ângulo sólido subtende toda
a área superficial da esfera, e vale 4
radianos; o maior ângulo sólido subtende toda
a área superficial da esfera, e vale 4![]() esferorradianos.
esferorradianos.
Quando a luz é emitida de uma fonte isotrópica (que emite igualmente em
todas as direções),
ela se expande esfericamente. É como
se a fonte estivesse no centro de uma esfera, composta de 4![]() ângulos
sólidos unitários, e cujo raio vai aumentando à medida que a luz se
propaga.
A energia que atravessa a unidade de área da fonte, por unidade
de tempo e por unidade de ângulo sólido, é chamada
intensidade específica:
ângulos
sólidos unitários, e cujo raio vai aumentando à medida que a luz se
propaga.
A energia que atravessa a unidade de área da fonte, por unidade
de tempo e por unidade de ângulo sólido, é chamada
intensidade específica:
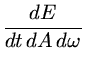
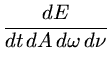
Num caso mais geral, a energia não se propaga isotrópicamente. (Por
exemplo, se observarmos a fonte através de um orifício em uma placa
opaca colocada na frente dela). Nesse caso, a energia que atravessa a
unidade de área não é a mesma em todas as direções, mas vai
depender do ângulo (![]() ) entre a direção de propagação
e a normal à área, ou seja:
) entre a direção de propagação
e a normal à área, ou seja:
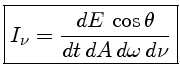 |
(1) |
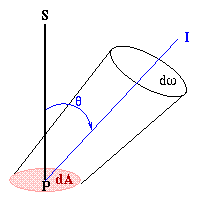
Na figura acima, a intensidade na direção de S é diferente do que
na direção de I, pois o elemento de área normal a I é
dA cos![]() .
.
Geralmente, a intensidade específica é medida em J m-2s-1sr-1Hz-1 no sistema MKS, ou erg cm-2s-1sr-1Hz-1 no sistema cgs.
Recapitulando, a intensidade específica monocromática
![]() é a
energia por unidade de área e por unidade de tempo que está
sendo emitida pela fonte, em um
intervalo de freqüências
é a
energia por unidade de área e por unidade de tempo que está
sendo emitida pela fonte, em um
intervalo de freqüências ![]() .
Na posição do observador, essa energia
é captada ao longo de uma direção
.
Na posição do observador, essa energia
é captada ao longo de uma direção ![]() , que é o ângulo
entre a linha de visada e a direção normal à superfície
emissora, e dentro de um ângulo sólido
, que é o ângulo
entre a linha de visada e a direção normal à superfície
emissora, e dentro de um ângulo sólido ![]() , que será tanto
menor quanto mais distante estiver o objeto. Formalmente, a
intensidade específica é definida como a energia que atravessa
um elemento de área dA, por intervalo de tempo, dentro de um
elemento de ângulo sólido
, que será tanto
menor quanto mais distante estiver o objeto. Formalmente, a
intensidade específica é definida como a energia que atravessa
um elemento de área dA, por intervalo de tempo, dentro de um
elemento de ângulo sólido
![]() ,
na direção
,
na direção ![]() ,
dentro de um intervalo de freqüências
,
dentro de um intervalo de freqüências ![]() e
e ![]() .
.
A intensidade específica, por sua definição, não depende da distância da fonte emissora, se não houverem fontes ou absorsores de radiação ao longo da linha de visada. Geralmente é medida em J m-2 s-1 sr-1 Hz-1 no sistema MKS ou ergs cm-2 s-1 sr-1 Hz-1 no sistema cgs. Um sr, chamado de esferorradiano, é uma unidade de ângulo sólido.
Podemos também definir a intensidade específica monocromática
por intervalo de comprimento de onda, lembrando que, por definição:
![]()
A intensidade específica integrada em todo o espectro de
freqüências é dada por:
![]()
Fluxo
Outra quantidade de grande interesse é o fluxo F, que é
a energia por unidade de área e por unidade de tempo que chega ao
detector, e é o que se mede realmente. Formalmente, o fluxo
em uma certa freqüência, em um
dado ponto e em uma dada direção, é a quantidade líquida de
energia radiante cruzando a unidade de área, por unidade de tempo,
e por intervalo de freqüência,
ou seja,
![]()
Escrevendo o ângulo sólido explicitamente
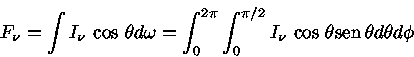
|
(2) |
O fluxo portanto significa potência através de uma superfície, e é expresso em erg cm-2s-1, ou em watts/m2.
Ao contrário da intensidade específica, o fluxo de radiação
cai com o quadrado da distância (r), de forma que o fluxo que chega na
Terra é muito menor do que o fluxo na superfície do astro, estando
diluído por um fator de ![]() .
.
Para uma estrela esférica de raio R, o fluxo na sua superfície
será
![]()
onde
L=Luminosidade.
A
luminosidade
é a energia total emitida por
segundo em todas as direções.
O fluxo a uma distância r da estrela será
![]()
Nesse caso, F(r) é o fluxo integrado sobre toda a superfície da estrela, e a luminosidade da estrela L pode ser obtida diretamente multiplicando o fluxo dela proveniente pela área sobre a qual o fluxo se distribui, integrado sobre todas as freqüências.
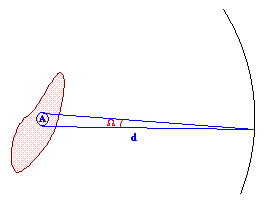
Para objetos extensos (os que não têm aparência estelar), podemos
definir ainda o brilho superficial, que é o fluxo captado
pelo observador dentro de um ângulo sólido unitário (brilho = ![]() ).
Aqui o ângulo sólido
).
Aqui o ângulo sólido ![]() tem vértice no observador e é subentendido
pela área A no objeto e, portanto, o brilho superficial é brilho
por unidade de área angular. Assim como a intensidade específica,
o brilho superficial não depende da distância, pois tanto o fluxo
F como o ângulo sólido
tem vértice no observador e é subentendido
pela área A no objeto e, portanto, o brilho superficial é brilho
por unidade de área angular. Assim como a intensidade específica,
o brilho superficial não depende da distância, pois tanto o fluxo
F como o ângulo sólido ![]() diminuem com o quadrado da
distância entre o objeto e o observador.
diminuem com o quadrado da
distância entre o objeto e o observador.
O brilho aparente de um astro é
o fluxo medido na Terra e,
normalmente, é expresso
em termos da magnitude aparente m, que por definição
é dada por:
![]()
Porque o brilho de um astro é medido em magnitudes? Há 2000 anos, o grego Hiparco (160-125 a.C.) dividiu as estrelas visíveis a olho nu de acordo com seu brilho aparente, atribuindo magnitude 1 à mais brilhante e 6 às mais fracas. Na definição de Hiparco, as de magnitude=1 são as vinte primeiras estrelas que aparecem após o pôr-do-sol.
Em 1856, Norman Robert Pogson (1829-1891) verificou
que o sistema, baseado na percepção de brilho do olho
humano, é logarítmico, e o fluxo correspondente
a uma estrela de primeira magnitude (m=1) era 100 vezes
mais brilhante que uma estrela de magnitude 6, de modo que:
![]()
![]()
como na definição acima. Logo:
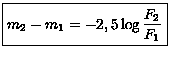
Mais precisamente, 2,5125=100. A constante const. na definição de magnitude acima define o ponto zero da escala. Normalmente utiliza-se a magnitude aparente da estrela Vega como m=0. Vega é uma estrela B9.5IV-V, com Tef=10 105±230 K e R=2.69±0.25RSol, a 7.76 pc.
![]()
onde ![]() é o fluxo no comprimento
de onda efetivo do filtro.
é o fluxo no comprimento
de onda efetivo do filtro.




| Cor | Comprimento de onda | Do espaço | Lua Nova | Lua Cheia |
|---|---|---|---|---|
| U | 3700Å | 23,2 | 22,0 | |
| B | 4400Å | 23,4 | 22,7 | 19.4 |
| V | 5500Å | 22,7 | 21,8 | 19,7 |
| R | 6400Å | 22,2 | 20,9 | 19,9 |
| I | 8000Å | 22,2 | 19,9 | 19,2 |
| J | 1,2 |
20,7 | 15,0 | 15,0 |
| H | 1,6 |
20,9 | 13,7 | 13,7 |
| K | 2,2 |
21,3 | 12,5 | 12,5 |
Para objetos extensos costuma-se definir a magnitude integrada como:
![]()
onde, supondo simetria esférica:
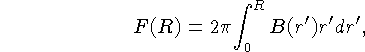
e onde B(r') é o brilho superficial em r'.
A magnitude aparente total de um objeto extenso em princípio é obtida integrando seu fluxo até um raio infinito:
![]()
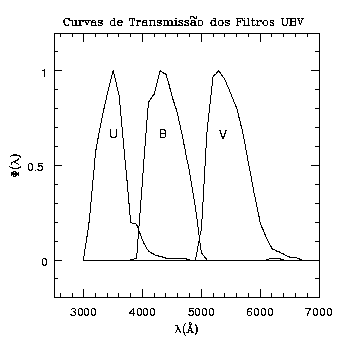
 Um dos sistemas de banda intermediária mais usados é o definido em 1963 pelo
dinamarquês Bengt Georg Daniel Strömgren (1908-1987),
no Quarterly Journal of the Royal Astronomical Society, 4, 8,
consistindo de
filtros com largura entre 180 e 300 Å, centrados em
3500, 4110, 4670 e 5470 Å, cujas magnitudes são chamadas: u, v, b e y.
[Begnt Strömgren. Spectral Classification Through Photoelectric Narrow-Band Photometry, Annual Review of Astronomy and Astrophysics, 4, 433-72 (1966).]
Um dos sistemas de banda intermediária mais usados é o definido em 1963 pelo
dinamarquês Bengt Georg Daniel Strömgren (1908-1987),
no Quarterly Journal of the Royal Astronomical Society, 4, 8,
consistindo de
filtros com largura entre 180 e 300 Å, centrados em
3500, 4110, 4670 e 5470 Å, cujas magnitudes são chamadas: u, v, b e y.
[Begnt Strömgren. Spectral Classification Through Photoelectric Narrow-Band Photometry, Annual Review of Astronomy and Astrophysics, 4, 433-72 (1966).]
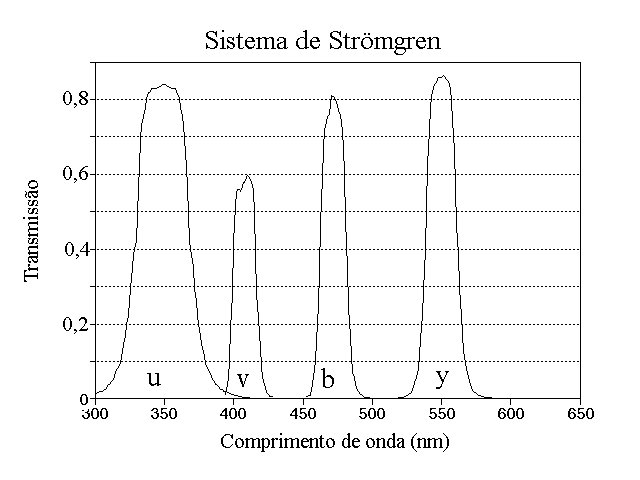
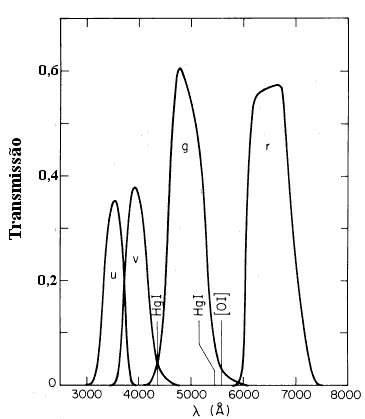
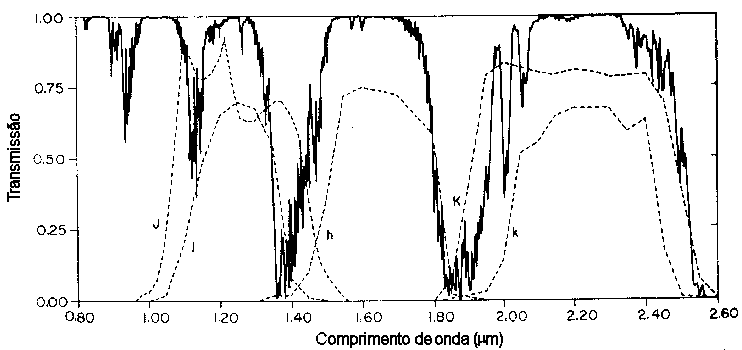
Johannes Nendwich, U. Heiter, F. Kupka, N. Nesvacil e Werner W. Weiss, publicaram no Communications in Asteroseismology, 144, 43 (2004) as curvas de transmissão de 14 sistemas fotométricos.
Dois sistemas de magnitude são o STMAG e o
AB![]() , que definem a constante de
conversão de magnitude para fluxo:
, que definem a constante de
conversão de magnitude para fluxo:
Os modelos de atmosfera nos dão o fluxo na superfície da estrela, ![]() .
O fluxo observado é dado por
.
O fluxo observado é dado por
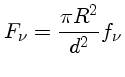
A magnitude da estrela é então dada por
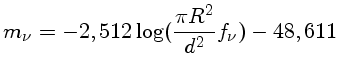
![$M_\nu = -2,512 \log [\frac{\pi R^2}{(10{pc})^2}
10^{(\frac{m_\nu+48.611}{-2,512})}] - 48,611$](../ccd/ruido/img7g.png)
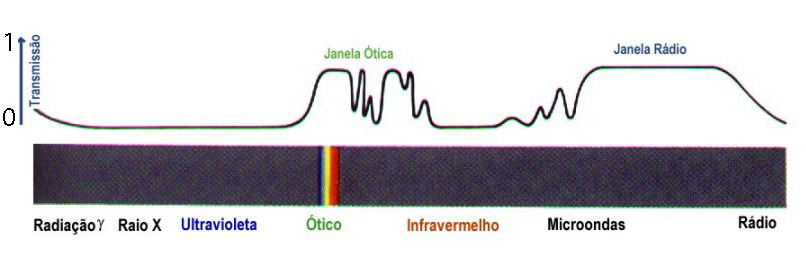
Embora a atmosfera seja praticamente transparente na faixa visível (3500 Å a 6500 Å), ela absorve fortemente no ultravioleta (1000 Å a 3500 Å) e em várias bandas do infra-vermelho (1 μm a 1 mm), de modo que não podemos medir ultravioleta do solo, e infra-vermelho somente acima de 2000 m de altura.
Na atmosfera existem vários componentes que difundem a luz em todas as direções (moléculas, partículas sólidas de poeira e fumaça), causando uma extinção contínua, em todos os comprimentos de onda. A extinção é tanto maior quanto maior for a quantidade de ar atravessada pela luz. É por este motivo que podemos olhar diretamente para o Sol no horizonte.
A atmosfera da Terra afeta as medidas, de forma que as magnitudes observadas devem ser ajustadas aos valores que teríamos se as observações fossem feitas fora da atmosfera. O efeito da atmosfera é absorver e espalhar a radiação em outras direções, processos esses que são descritos por um coeficiente de absorção k, usualmente medido em cm-1.
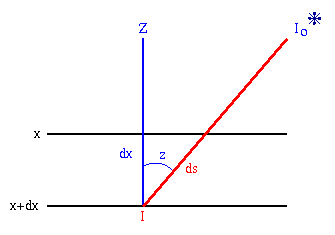
Podemos expressar a extinção atmosférica em função da massa de ar atravessada pelo raio luminoso.
![]()
![]()
Como
![]() onde z
é a distância zenital,
onde z
é a distância zenital,
![]()
Imaginemos a atmosfera como uma camada de altura H, Fo o fluxo no topo da atmosfera e F o que chega ao observador. Então,
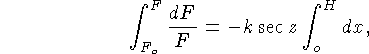
![]()
A espessura ótica é uma função da distância zenital z, e
supondo que a camada atmosférica é formada por camadas
plano-paralelas, ela pode ser expressa por
![]() onde
onde ![]() = kH
é a espessura ótica na direção do zênite, e o
fluxo será:
= kH
é a espessura ótica na direção do zênite, e o
fluxo será:
![]()
Em magnitudes, essa equação fica:
![]()
![]()
onde ![]() é o coeficiente de extinção, e
é o coeficiente de extinção, e
![]() é a massa de ar.
é a massa de ar.
Um exemplo de aplicação deste conceito é considerarmos uma estrela observada a uma distância zenital de 45°. Como sec 45°= 1,41 e usando um coeficiente kH = 0,46, típico de observações óticas, obtemos F = 0,52 Fo, ou seja, a atmosfera terrestre absorve 48% da luz da estrela ao observarmos a 45° do zênite.
A diferença (m - mo) é a extinção atmosférica em magnitudes, e é determinada através de estrelas padrões para as quais mo é conhecido.
A constante K é característica do meio, e depende do comprimento de onda, sendo mais correto escrever
![]()
Para o sistema UBV, e para locais situados acima de 1500 m de altitude,
Se observarmos uma estrela a 45° do zênite, vemos que a extinção atmosférica neste caso equivale a 1,48 sec 45°=2,09 mag em U, 0,56 sec 45°=0,79 mag em B e 0,40 sec 45°=0,57 mag em V.
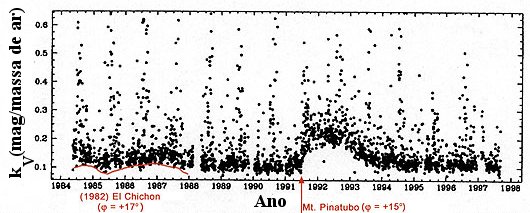
Além da extinção atmosférica, é necessário levar em conta também a extinção interestelar, devida à poeira interestelar concentrada principalmente no plano da Galáxia, e que também extingue a luz das estrelas. A extinção interestelar depende da direção em que se encontra o objeto, visto que a distribuição de matéria na nossa galáxia é não homogênea. A luz provinda de outras galáxias também sofre extinção dentro das próprias galáxias.
Se não existisse extinção, a magnitude visual absoluta MV de uma estrela de magnitude aparente Vo, localizada a uma distância d seria:
|
Considerando que a magnitude aparente V está afetada por avermelhamento, Vo=V-AV, e a magnitude visual absoluta será:
|
Similarmente, a magnitude azul absoluta será:
|
|
|
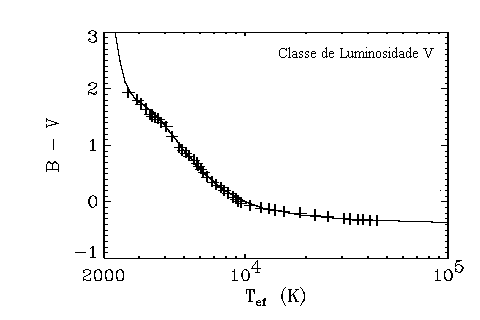
Vemos assim que, embora a magnitude aparente uma estrela dependa de sua distância, o índice de cor não depende da distância e, por isso, é muito útil para determinar a temperatura da estrela.
A extinção interestelar em magnitudes é representada pela letra A com um subscrito indicando a banda espectral a que se refere, por exemplo, a extinção interestelar na banda B é AB e na banda V é AV.![A_{\lambda_1}-A_{\lambda_2} = 2,5 \{\log\[\frac{F_0\(\lambda_1\)}{F_0\(\lambda_2\)}\] - \log\[\frac{F\(\lambda_1\)}{F\(\lambda_2\)}\]\}](alambda.png)
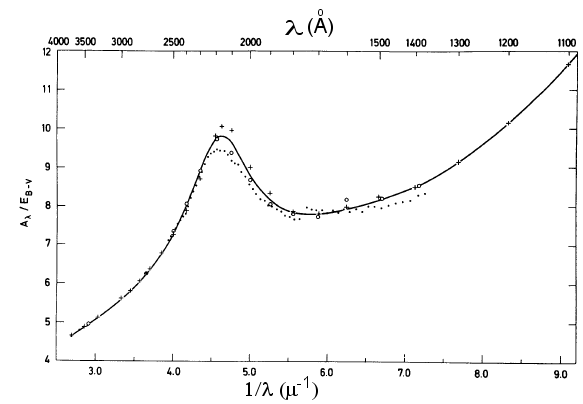
Na ausência de avermelhamento interestelar, as cores (B-V) e (U-B) das estrelas (não da lei de Planck) se encontram em um curva ondulada.
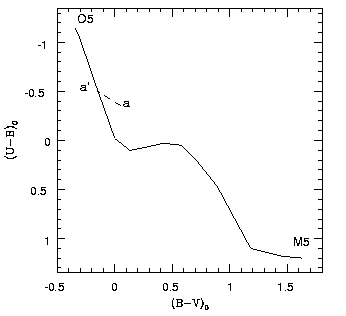
Se a estrela a é encontrada fora desta curva, assumimos que ela sofreu avermelhamento interestelar e movemos a medida para cima ao longo da diagonal de inclinação conhecida
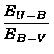 = 0, 72
= 0, 72
A correção ao fluxo observado em V, FVobs, também pode ser obtida do avermelhamento, já que a poeira interestelar produz uma razão constante de fluxos:
O valor de R está entre 3,0 e 5,0, dependendo da direção na Galáxia.
Desta maneira podemos obter os valores reais dos fluxos, isto é, os fluxos corrigidos pelo avermelhamento interestelar, e medir não somente a temperatura, mas também estimar a correção bolométrica C.B., que definimos como:
| Tipo | (B - V)0 | (U - B)0 | Tef | C.B. | MBol | Massa
( |
|---|---|---|---|---|---|---|
| O5 | -0,35 | -1,15 | 40000 | 4,00 | -10,0 | 120 |
| B0 | -0,31 | -1,06 | 28000 | 2,80 | -6,8 | 17 |
| B5 | -0,16 | -0,55 | 15500 | 1,50 | -2,6 | 6 |
| A0 | 0,00 | -0,02 | 9900 | 0,40 | 0,1 | 2,9 |
| A5 | 0,13 | 0,10 | 8500 | 0,12 | 1,7 | 2,2 |
| F0 | 0,27 | 0,07 | 7400 | 0,06 | 2,6 | 1,6 |
| F5 | 0,42 | 0,03 | 6580 | 0,00 | 3,4 | 1,25 |
| G0 | 0,58 | 0,05 | 6030 | 0,03 | 4,3 | 1,1 |
| G5 | 0,70 | 0,19 | 5520 | 0,07 | 5,0 | 0,9 |
| K0 | 0,89 | 0,47 | 4900 | 0,19 | 5,8 | 0,8 |
| K5 | 1,18 | 1,10 | 4130 | 0,60 | 6,7 | 0,65 |
| M0 | 1,45 | 1,18 | 3480 | 1,19 | 7,8 | 0,5 |
| M5 | 1,63 | 1,20 | 2800 | 2,30 | 9,8 | 0,15 |
Como uma estrela não é um corpo negro, isto é, suas camadas externas de onde provém a radiação não estão exatamente em equilíbrio térmico, escrevemos para o fluxo da estrela:
definindo um parâmetro chamado temperatura efetiva Tef. Portanto, para uma estrela esférica de raio R, a luminosidade (energia total por segundo) é obtida multiplicando-se o fluxo pela área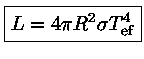
A temperatura efetiva de uma estrela é portanto a temperatura de um corpo negro que emite a mesma quantidade de energia por unidade de área e por unidade de tempo.
A luminosidade do Sol, isto é, a energia total
emitida pelo Sol é ![]() ,
sendo que 1 Joule = 107 ergs.
,
sendo que 1 Joule = 107 ergs.
Como o raio do Sol é de ![]() 700 000 km,
segue
que a temperatura efetiva do Sol é
Tef
700 000 km,
segue
que a temperatura efetiva do Sol é
Tef![]() = 5400K.
= 5400K.
Podemos escrever a Lei de Wien aproximadamente como
A definição de temperatura de um objeto astronômico não é única, pois depende do método que estamos usando para medi-la. Assim, a temperatura de uma estrela medida pela lei de Wien (a partir da intensidade em um comprimento de onda), é ligeiramente diferente da sua temperatura medida pela lei de Stefan-Boltzmann (a partir da luminosidade e do raio). Esta última é chamada temperatura efetiva, enquanto a primeira é chamada temperatura de brilho. Pode-se ainda definir a temperatura de cor, determinada a partir da razão de fluxos em dois comprimentos de onda diferentes. Essas temperaturas não são iguais porque os corpos astronômicos não são corpos negros perfeitos.
Esse caso, que ocorre na atmosfera de uma estrela, é chamado equilíbrio termodinâmico local. É um conceito importante na teoria de interiores de estrelas e evolução estelar.
As camadas mais internas das estrelas são mais quentes e emitem mais radiação que as camadas mais externas. Assim, a luz (ou melhor, a radiação, pois a maior parte não é visível), sai de uma camada quente mais interna [chamemos de camada (n-1)], passa pela camada considerada (n) e atinge uma camada FRIA mais externa (n+1). Para haver equilíbrio, isto é, para a temperatura se manter, será necessário que a energia que entra, vinda da camada (n-1), seja transmitida para a camada (n+1), sem ficar "depositada" na camada n e aumentar sua temperatura. Isso, porém, não significa que a camada n é transparente, mas que a radiação vai fluir do interior da estrela para fora. Aliás, no interior da estrela, a radiação vai se deslocar somente uns poucos centímetros antes de ser reabsorvida. Mas depois ela será re-emitida em todas as direções e vai fazer um caminho em zig-zag lentamente até a superficie da estrela.
Assim, o resultado final é que a energia gerada nas reações nucleares no núcleo da estrela vai acabar sendo emitida na superfície da estrela, passando pelas camadas intermediárias sem alterar significativamente a distribuição de temperatura dessas camadas. Isso é bem diferente do equilíbrio termodinâmico per se, em que as todas as camadas têm a mesma temperatura.
O espectro emitido no centro da estrela, pelas reações nucleares, é "duro", de raios gama, mas logo vai ser "abrandado" ou ficar mais "mole" (de comprimento de onda maior e energia menor por "fóton"). Como a energia total se mantem e cada fóton tem menos energia, o número de fótons é muito maior. Nesse processo, que envolve um enorme número de eventos ou colisões entre os fótons e a matéria, o espectro será contínuo, distribuído em todas as freqüências. Ao migrar para camadas mais externas e frias, o espectro se torna cada vez mais "mole", passando a ser principalmente em raios X, ultravioleta e, finalmente, perto da superfície, no vísivel.
A "superfície" de uma estrela (fotosfera) não é
uma camada de propriedades químicas
e físicas distintas, como nos planetas. Toda a estrela é um gás, que
absorve e reemite a radiação, de acordo com a sua temperatura.
Mais no centro,
o gás (na maioria hidrogênio e hélio) está todo ionizado,
sendo composto de núcleos
e elétrons livres. Porém a temperatura é menor na superfície,
havendo
átomos que podem ter elétrons em diferentes energias. Mas os elétrons
não podem ficar em qualquer nível de energia -
é um fato básico e muito
intrigante. Eles só "aceitam" energia de comprimento de onda bem
determinado (6563 Å, da linha
H![]() ,
por exemplo, no átomo de H)
e então
"pulam" para um nível mais alto,
absorvendo o fóton dessa energia. Não "servem"
os fótons de menos energia, nem tampouco os de mais energia, a não ser de
energia bem maior, que permite "pular" dois níveis para cima. Assim,
quando a radiação passa pela camada externa (menos densa e mais fria)
os átomos dessa camada vão absorver apenas os fótons de comprimentos de
onda característicos, que serão removidos da radiação
que se desloca
da camada mais interna para fora da estrela. Além da fotosfera,
o gás está tão rarefeito que, na prática,
não mais absorve a radiação visível.
Assim, a "superfície" é apenas um
fenômeno ótico, relacionado com a emissão e absorção
da luz da estrela.
,
por exemplo, no átomo de H)
e então
"pulam" para um nível mais alto,
absorvendo o fóton dessa energia. Não "servem"
os fótons de menos energia, nem tampouco os de mais energia, a não ser de
energia bem maior, que permite "pular" dois níveis para cima. Assim,
quando a radiação passa pela camada externa (menos densa e mais fria)
os átomos dessa camada vão absorver apenas os fótons de comprimentos de
onda característicos, que serão removidos da radiação
que se desloca
da camada mais interna para fora da estrela. Além da fotosfera,
o gás está tão rarefeito que, na prática,
não mais absorve a radiação visível.
Assim, a "superfície" é apenas um
fenômeno ótico, relacionado com a emissão e absorção
da luz da estrela.
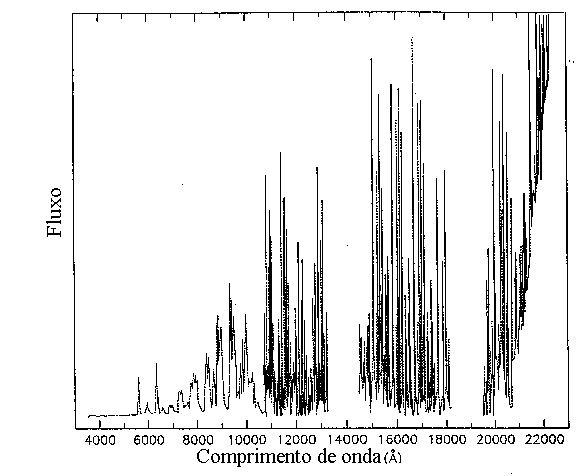
Portanto, superpostas na radiação contínua emitida pela estrela, aparecem linhas escuras (linhas de Fraunhofer, que as identificou, classificou e estudou a partir de 1814), características dos elementos químicos das camadas superficiais da estrela. Porém, o gás que absorve a luz também se aquece. Na fotosfera do Sol, a temperatura é superior a 5000 K. As linhas escuras nunca são totalmente escuras ou desprovidas de luz. Elas têm a contribuição da luz emitida pelo gás que absorve a luz, mas que também a reemite.
![]() Ruído nas medidas
Ruído nas medidas
![]() Astronomia e Astrofísica
Astronomia e Astrofísica
![]()
©