| Fluxo | Magnitude | Absoluta | Bolométrica | Extinção | Radiação | Wien | Steffan-Boltzmann |

As observações com satélites, balões e espaçonaves são feitas fora da atmosfera, mas a grande maioria das observações é obtida da superfície da Terra.
Como a maioria das observações utiliza radiação electromagnética, e podemos obter informações sobre a natureza física da fonte estudando a distribuição de energia desta radiação, introduziremos alguns conceitos para a caracterização desta radiação.
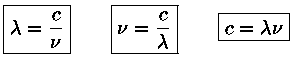
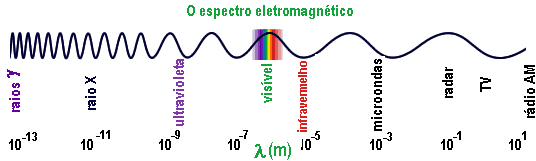
Localização no espectro:
A radiação visível vai aproximadamente de 3900 Å (violeta) até cerca de 7800 Å (vermelho).
| Cor | Comprimento de onda (Å) | Freqüência (1012 Hz) |
|---|---|---|
| violeta | 3900 - 4550 | 659 - 769 |
| azul | 4550 - 4920 | 610 - 659 |
| verde | 4920 - 5770 | 520 - 610 |
| amarelo | 5770 - 5970 | 503 - 520 |
| laranja | 5970 - 6220 | 482 - 503 |
| vermelho | 6220 - 7800 | 384 - 482 |
A grandeza mais característica de um campo de radiação é uma constante chamada intensidade específica monocromática. Para melhor entender esse conceito, vamos antes revisar o conceito de ângulo sólido.
Assim como podemos entender um ângulo plano α como um setor de um círculo, definido como a razão entre o arco a e o raio do círculo r, podemos entender um ângulo sólido ω como um "setor" de uma esfera, definido pela razão entre o elemento de área na superfície da esfera A e o seu raio ao quadrado r2:

O maior ângulo plano é aquele que subtende toda a circunferência do círculo, e vale 2π radianos; o maior ângulo sólido subtende toda a área superficial da esfera, e vale 4π esferorradianos (sr).
Quando a luz é emitida de uma fonte isotrópica - que emite igualmente em todas as direções -, ela se expande esfericamente. É como se a fonte estivesse no centro de uma esfera, composta de 4π ângulos sólidos unitários, e cujo raio vai aumentando à medida que a luz se propaga. A energia que atravessa a unidade de área da fonte, por unidade de tempo, perpendicular à área dA, e por unidade de ângulo sólido, é chamada intensidade específica:
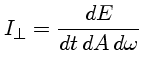
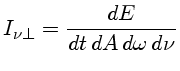
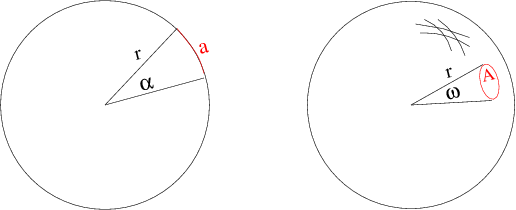
Num caso mais geral, a energia não se propaga isotrópicamente. Por exemplo, se observarmos um facho de um projetor ou um feixe de laser, ou um pulsar. Nesse caso, a energia que atravessa a unidade de área não é a mesma em todas as direções, mas vai depender do ângulo (θ) entre a direção de propagação e a normal à área, ou seja:
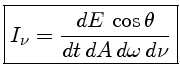 |
(1) |
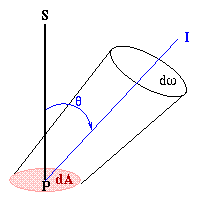
Na figura acima, a intensidade na direção de S é diferente do que na direção de I.
Geralmente, a intensidade específica é medida em J m-2 s-1 sr-1 Hz-1 no sistema MKS, ou erg cm-2 s-1 sr-1 Hz-1 no sistema cgs.
Recapitulando, a intensidade específica monocromática Iν é a energia por unidade de área e por unidade de tempo que está sendo emitida pela fonte, em um intervalo de freqüências dν. Na posição do observador, essa energia é captada ao longo de uma direção θ, que é o ângulo entre a linha de visada e a direção normal à superfície emissora, e dentro de um ângulo sólido dω, que será tanto menor quanto mais distante estiver o objeto. Formalmente, a intensidade específica é definida como a energia que atravessa um elemento de área dA, por intervalo de tempo, dentro de um elemento de ângulo sólido dω=senθdθdφ, na direção θ dentro de um intervalo de freqüências ν e ν+dν.
A intensidade específica, por sua definição dentro de um feixe, não depende da distância da fonte emissora, se não houverem fontes ou absorsores de radiação ao longo da linha de visada.
Podemos também definir a intensidade específica monocromática
por intervalo de comprimento de onda, lembrando que, por definição:
![]()
A intensidade específica integrada em todo o espectro de
freqüências é dada por:
![]()
Fluxo
Outra quantidade de grande interesse é o fluxo F, que é
a energia por unidade de área e por unidade de tempo que chega ao
detector, e é o que se mede realmente. Formalmente, o fluxo
em uma certa freqüência, em um
dado ponto e em uma dada direção, é a quantidade líquida de
energia radiante cruzando a unidade de área, por unidade de tempo,
e por intervalo de freqüência,
ou seja,
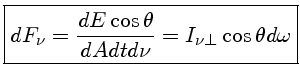
|
(2) |
Escrevendo o ângulo sólido dω explicitamente
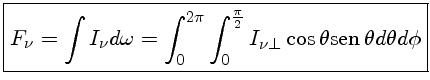
O fluxo portanto significa potência através de uma superfície, e é expresso em erg cm-2 s-1, ou em watts/m2.
Ao contrário da intensidade específica, por não estar mais em um feixe, o fluxo de radiação
cai com o quadrado da distância à fonte (r), de forma que o fluxo que chega na
Terra é muito menor do que o fluxo na superfície do astro, estando
diluído por um fator de ![]() .
.
Para uma estrela esférica de raio R, que emite homogeneamente em todas as direções, o fluxo na sua superfície
será
![]()
logo
![]() onde
L=Luminosidade,
é a energia total emitida por segundo em todas as direções.
onde
L=Luminosidade,
é a energia total emitida por segundo em todas as direções.
O fluxo a uma distância r da estrela será
![]()
Nesse caso, F(r) é o fluxo integrado sobre toda a superfície da estrela, e a luminosidade da estrela L pode ser obtida diretamente multiplicando o fluxo dela proveniente pela área sobre a qual o fluxo se distribui, integrado sobre todas as freqüências.
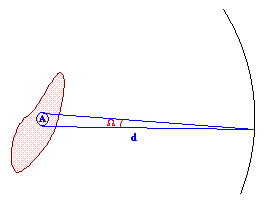
O brilho aparente de um astro é o fluxo medido na Terra e, normalmente, é expresso em termos da magnitude aparente m, que por definição é dada por:
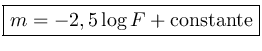
Em 1856, o astrônomo inglês
Norman Robert Pogson
(1829-1891), do Observatório Radcliffe, em Oxford,
propos
que o sistema de magnitudes, baseado na percepção de brilho do olho
humano, é logarítmico, e o fluxo correspondente
a uma estrela de primeira magnitude (m=1) era 100 vezes
mais brilhante que uma estrela de magnitude 6
(Magnitudes of Thirty-six of the Minor Planets for the first day of each month of the year 1857,
1856, Monthly Notices of the Royal Astronomical Society, 17, p. 12),
de modo que:
![]()
![]()
como na definição acima.
Ou seja, por ter escala logarítmica, comprovado experimentalmente em 1834 pelo fisiologista alemão Ernst Heinrich Weber (1795-1878) e seu estudante Gustav Theodor Fechner (1801-1887) e publicado em 1860
(Elemente der Psychophysik, Leipzig: Breitkopf und Härtel),
o olho humano consegue ver coisas
100× mais fracas que as mais brilhantes.
Logo:
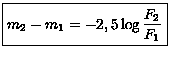
Mais precisamente, 2,5125=100. A constante na definição de magnitude acima define o ponto zero da escala, isto é, o fluxo correspondente a m=0. Normalmente utiliza-se a magnitude aparente da estrela Vega como m=0, o que define a constante da magnitude. Vega é uma estrela B9.5IV-V, com Tef=10 105±230 K e R=2,69±0,25 RSol, a 7,76 pc.
Para comparação,
| Magnitude Aparente | Visível na constelação | Diâmetro Aparente |
|---|---|---|
| m(Lua)= -11,14 | em Leão | 1784,3" |
| m(Mercúrio)= -0,21 | em Peixes | 6,1" |
| m(Vênus)= -4,68 | em Peixes | 32,9" |
| m(Marte)=1,04 | em Câncer | 6,3" |
| m(Júpiter)= -1,96 | em Touro | 32,6" |
| m(Saturno)=1,16 | em Peixes | 15,7" |
| m(Urano)=5,85 | em Touro | 3,4" |
| m(Netuno)=7,81 | em Peixes | 2,2" |
| m(Plutão)=14,52 | em Capricórnio | 0,003" |
A pupila do olho humano, quando adaptada ao escuro, tem aproximadamente 8 mm. Um telescópio com 8 cm de diâmetro, tem uma área (80 mm/8 mm)2=100 vezes maior e portanto capta 100 vezes mais fótons. Desta maneira este telescópio de 8 cm de abertura permite observar 5 magnitudes mais fracas do que o olho humano, ou seja, até magnitude 6+5=11, no tempo de integração do olho humano, de 0,015 s (cones) a 0,1 segundos (bastões). Normalmente leva 25 minutos para o olho humano tornar-se completamente adaptado ao escuro, isto é, com a pupila completamente dilatada. Para um campo de vista restrito, experimentos conduzidos por Heber Curtis e Henry Norris Russel no início dos anos 1900, mostraram que um olho completamente adaptado ao escuro olhando uma pequena área do céu, de 5 minutos de arco de extensão, conseguia detectar estrelas até magnitude +8,5, correspondendo a aproximadamente 200 fótons por segundo.
Como um telescópio tem uma área coletora maior do que um olho, pode coletar mais energia de um objeto com um determinado fluxo, de modo que o objeto parece mais brilhante quando visto pelo telescópio. Se uma estrela tem um fluxo Fo vista com o olho nu, então se vista por um telescópio aparecerá com um fluxo Ft dado por:
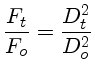
![]()
onde F(λo)
é o fluxo no comprimento
de onda efetivo do equipamento.




| Cor | Comprimento de onda | Do espaço | Lua Nova | Lua Cheia |
|---|---|---|---|---|
| U | 3700Å | 23,2 | 22,0 | 17,0 |
| B | 4400Å | 23,4 | 22,7 | 19,5 |
| V | 5500Å | 22,7 | 21,8 | 20,0 |
| R | 6400Å | 22,2 | 20,9 | 19,9 |
| I | 8000Å | 22,2 | 19,9 | 19,2 |
| J | 1,2μm | 20,7 | 15,0 | 15,0 |
| H | 1,6μm | 20,9 | 13,7 | 13,7 |
| K | 2,2 |
21,3 | 12,5 | 12,5 |
Para estrelas quentes, entre 30 000 K ⦥ Tef ⦥ 9500 K, Ralf Napiwotski, Detlef Schönberner & Verena Wenske (1993, Astronomy & Astrophysics, 268, 653) estabeleceram uma relação entre a temperatura efetiva e o índice de cor Ströngren corrigido por avermelhamento [u-b]=(u-b)-1,53(b-y):
A magnitude aparente (m) de uma estrela mede seu brilho aparente, que depende de sua distância. Por exemplo, qual estrela é intrinsicamente mais brilhante, Sírius, com m=-1,42 ou Vega, com m=0? Claro que visto aqui da Terra, Sírius é mais brilhante. Para podermos comparar os brilhos intrínsecos de duas estrelas, precisamos usar uma medida de brilho que independa da distância. Para isso, definimos como magnitude absoluta (M), a magnitude teórica que a estrela teria se estivesse a 10 parsecs de nós.
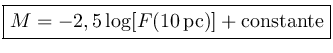
![m-M = -2,5 \log [F(r)] + 2,5 \log [F(10~pc)] = -2,5 \log \frac{F(r)}{F(10~pc)}](img462.gif)
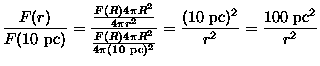
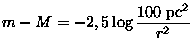
| m - M = 5 log r -5 |
Logo,
Na nomenclatura usual, V=mv, B e U são magnitudes aparentes e as magnitudes absolutas correspondentes são MV, MB e MU.
| Ordem | Estrela | Magnitude Absoluta MV | Magnitude Aparente mV | Distância à Terra (anos-luz) |
Tipo Espectral | B-V |
|---|---|---|---|---|---|---|
| 0 | Sol | +4,72 | -26,72 | 8 minutos | G2 V | 0,7 |
| 1 | Sírius (no Cão Maior) | +1,4 | -1,46 | 8,6 | A1 V | 0,00 |
| 2 | Canopus (na Carina) | -2,5 | -0,72 | 74 | F0 Ib | 0,16 |
| 3 | Rigel Kentaurus (Alpha Centauri) | +4,4 | -0,27 | 4,3 | G2 V | 0,7 |
| 4 | Arcturus (em Boötes) | +0,2 | -0,04 | 34 | K2 III | 1,23 |
| 5 | Vega (na Lyra) | +0,6 | 0,03 | 25 | AO V | 0,00 |
| 6 | Capella (na Auriga) | +0,4 | +0,08 | 41 | G2 III | 0,79 |
| 7 | Rigel (no Órion) | -8,1 | +0,12 | 900 | B8 Ia | -0,03 |
| 8 | Procyon (no Cão Menor) | 2,8 | +0,38 | 11 | F5 IV | 0,41 |
| 9 | Archenar (em Eridanus) | -1,3 | +0,46 | 75 | B5 IV | -0,18 |
| 10 | Betelgeuse (no Órion) | -5,1 | +0,58 | 445 | M2 I | 1,85 |
| 11 | Hadar (no Centauro) | -4,3 | +0,61 | 300 | B1 II | -0,23 |
| 12 | Altair (na Águia) | +2,3 | +0,77 | 17 | A7 V | 0,22 |
| 13 | Acrux (no Cruzeiro) | -3,8 | +0,79 | 270 | B2 IV | -0,26 |
| 14 | Aldebaran (em Touro) | -0,2 | +0,87 | 65 | K5 III | 1,54 |
| 15 | Spica (em Virgem) | -4,7 | +0,98 | 260 | B1 V | -0,24 |
| 16 | Antares (no Escorpião) | -5,2 | +1,09 | 600 | M1 Ib | 1,87 |
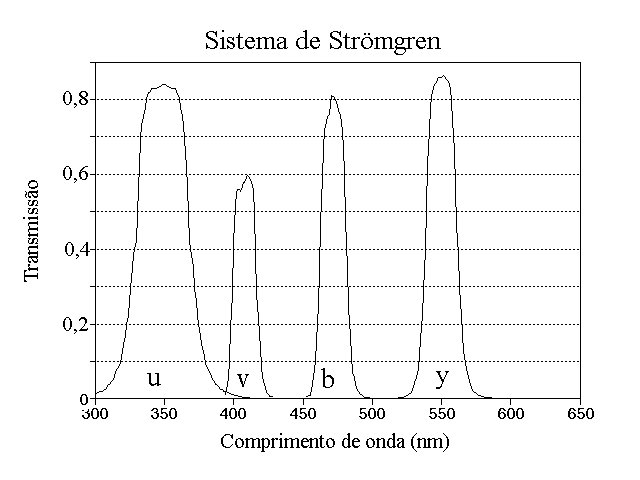
 Um dos sistemas de banda intermediária usados é o definido em 1963 pelo
dinamarquês Bengt Georg Daniel Strömgren (1908-1987)
(Quarterly Journal of the Royal Astronomical Society, 4, p. 8)
consistindo de
filtros com largura entre 180 e 300 Å, centrados em
3500, 4110, 4670 e 5470 Å, cujas magnitudes são chamadas: u, v, b e y
[Begnt Strömgren. Spectral Classification Through Photoelectric Narrow-Band Photometry, Annual Review of Astronomy and Astrophysics, 4, 433-72 (1966)].
Um dos sistemas de banda intermediária usados é o definido em 1963 pelo
dinamarquês Bengt Georg Daniel Strömgren (1908-1987)
(Quarterly Journal of the Royal Astronomical Society, 4, p. 8)
consistindo de
filtros com largura entre 180 e 300 Å, centrados em
3500, 4110, 4670 e 5470 Å, cujas magnitudes são chamadas: u, v, b e y
[Begnt Strömgren. Spectral Classification Through Photoelectric Narrow-Band Photometry, Annual Review of Astronomy and Astrophysics, 4, 433-72 (1966)].
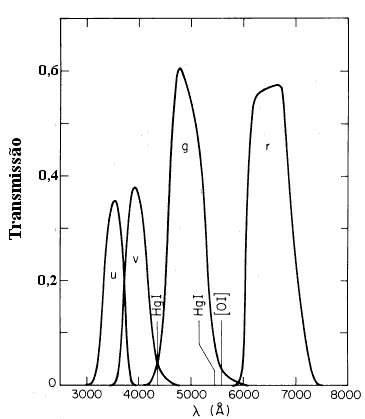
| Filtro | u | g | r | i | z |
|---|---|---|---|---|---|
| Comprimento de onda central (Å) | 3580 | 4900 | 6260 | 7670 | 9070 |
| Largura de banda (Å) | 640 | 1350 | 1370 | 1540 | 1470 |
Para Vega, no sistema do SDSS, assumindo V=+0.03 e U-B = B-V = V-Rc = Rc-Ic = 0.00, encontra-se
g = -0.08 (±0.03)
u-g = +1.02 (±0.08)
g-r = -0.25 (±0.03)
r-i = -0.23 (±0.02)
i-z = -0.17 (±0.02)
usando as transformações de Selcuk Bilir, S. Karaali, S. Tuncel (2005, Astronomische Nachrichten, 326, 5).
Para o Sol, assumindo MV=+4.82, U-B=+0.195, B-V=+0.650, V-Rc=+0.36, e Rc-Ic=+0.32, encontra-se:
M(g)= +5.12 (±0.02)
u-g = +1.43 (±0.05)
g-r = +0.44 (±0.02)
r-i = +0.11 (±0.02)
i-z = +0.03 (±0.02)
Para estrelas, Robert Lupton (2005) encontrou:
B = u - 0.8116*(u - g) + 0.1313; σ=0.0095 B = g + 0.3130*(g - r) + 0.2271; σ=0.0107 V = g - 0.2906*(u - g) + 0.0885; σ=0.0129 V = g - 0.5784*(g - r) - 0.0038; σ=0.0054 R = r - 0.1837*(g - r) - 0.0971; σ=0.0106 R = r - 0.2936*(r - i) - 0.1439; σ=0.0072 I = r - 1.2444*(r - i) - 0.3820; σ=0.0078 I = i - 0.3780*(i - z) -0.3974; σ=0.0063
O satélite Gaia mediu a distância e magnitude de 1,8 bilhões de estrelas, e seu sistema de magnitudes é definido em Gaia Data Release 3.
| Telescópio | Banda | λcentral(Å) | Sistema |
|---|---|---|---|
| GALEX | NUV | 2305 | AB |
| SDSS | u | 3562 | AB |
| g | 4719 | ||
| r | 6186 | ||
| i | 7500 | ||
| z | 8961 | ||
| APASS | JOHNSON B | 4347.53 | Vega |
| JOHNSON V | 5505 | ||
| Pan-STARRS | g | 4866 | AB |
| y | 9633 | ||
| Gaia | BP | 5129 | Vega |
| G | 6425 | ||
| RP | 7800 | ||
| TESS | red | 7972 | Vega |
| 2MASS | J | 12408 | Vega |
| H | 16514 | ||
| Ks | 21656 | ||
| ALLWISE | W1 | 33792 | Vega |
| W2 | 46293 | ||
| W3 | 123340 | ||
| W4 | 222530 |
Se tivéssemos equipamentos de fossem 100% sensíveis em todos os comprimentos de onda, teoricamente poderíamos medir o fluxo em todo o intervalo espectral. A magnitude correspondente à energia em todas as freqüências - desde os raios γ até as ondas de rádio - é chamada de magnitude bolométrica (aparente mbol e absoluta Mbol).
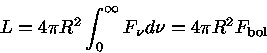
| mbol = mv - C.B. |
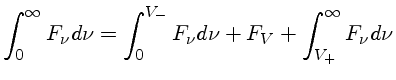
Como a magnitude absoluta bolométrica do Sol é ![]() ,
a magnitude absoluta bolométrica de uma estrela qualquer é dada por
,
a magnitude absoluta bolométrica de uma estrela qualquer é dada por
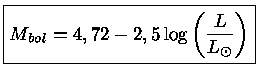
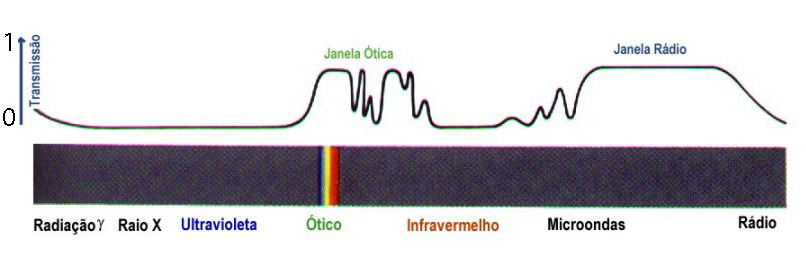
Embora a atmosfera seja praticamente transparente na faixa visível - 3500 Å a 6500 Å -, ela absorve fortemente no ultravioleta - abaixo de 3500 Å - e em várias bandas do infra-vermelho (1 μm a 1 mm), de modo que não podemos medir raios-γ, raios-X e ultravioleta do solo, e infra-vermelho somente acima de 2000 m de altura, até cerca de 1 mm→300 GHz (microondas), quando a ionosfera reflete as ondas incidentes. No rádio, a atmosfera é transparente de 100 GHz até 10 MHz. No ultravioleta, o ozônio (O3) e a água absorvem a luz. No raio-X, o efeito fotoelétrico com átomos de nitrogênio e oxigênio absorve a luz.
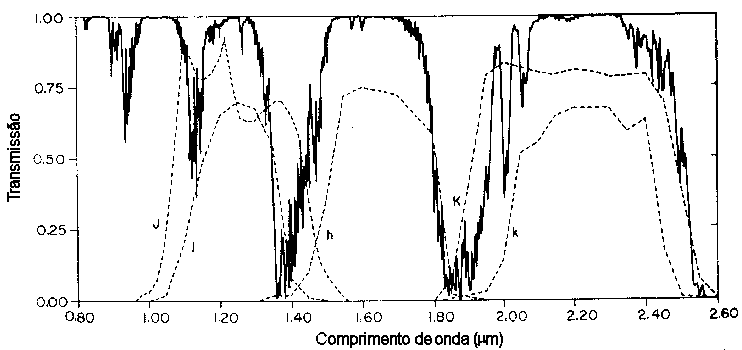
A absorção se dá por vários processos atômicos e moleculares. Absorções em freqüências particulares - linhas ou bandas - se dá por excitação de moléculas e átomos, enquanto ionização ou dissociação molecular leva a absorção contínua para todos as freqüências correspondentes a energia acima da energia necessária para separar os átomos ou moléculas. A extinção pela atmosfera da Terra, incluindo absorção e espalhamento, é total exceto nas janelas visual e rádio.
O espalhamento da radiação depende do comprimento de onda da radiação e do tamanho das partículas.
A janela rádio se estende entre aproximadamente 8 mm e 15 m, embora haja redução por vapor de água e moléculas de oxigênio (O2) para comprimentos de onda acima de 300 μm. O corte em comprimentos de ondas maiores se dá por reflexão crítica na ionosfera, uma camada da atmosfera acima de 100 km, onde há alta densidade de elétrons livres e íons. As ondas de rádio não podem penetrar neste plasma por que suas baixas freqüências estão abaixo da freqüência de plasma natural da ionosfera. Esta reflexão é entretanto usada para comunicação, refletindo as ondas de rádio na ionosfera. A atividade solar altera o nível de ionização da alta atmosfera, modificando as freqüências de reflexão.
A atmosfera da Terra não é estática nem horizontalmente estratificada. Ela está em constante movimento em várias escalas espaciais e temporais, desde as grandes e lentas causadas pelas frentes climáticas, até as rápidas e pequenas causadas por turbulência, devido a variações de temperatura e ventos. Estas mudanças constantes causam cintilação. Existem dois efeitos: variações da massa de ar no feixe causam flutuações na intensidade, enquanto variações no índice de refração ao longo do feixe causam variações na posição da imagem. Turbulência de pequena escala na atmosfera causa rápidas variações randômicas com escalas de segundos de arco na posição de imagens puntuais - a fonte se espalha em um disco aparente (seeing disk), se não for observada com resolução temporal da ordem de um centésimo de segundo. Esta cintilação é que limita o poder de resolução de telescópios na Terra. Os telescópios em Terra são limitados pelo seeing, e não por difração, no ótico. Como a massa de ar é maior no horizonte do que no zênite, a melhor observação é o mais próximo do zênite possível.
A atmosfera da Terra afeta as medidas, de forma que as magnitudes observadas devem ser ajustadas aos valores que teríamos se as observações fossem feitas fora da atmosfera. O efeito da atmosfera é absorver e espalhar a radiação em outras direções, processos esses que são descritos por um coeficiente de absorção k, usualmente medido em cm-1.
Podemos expressar a extinção atmosférica em função da massa de ar atravessada pelo raio luminoso.
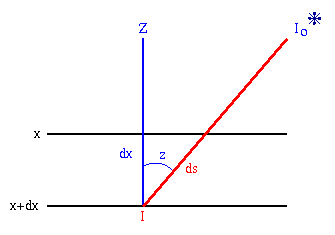
![]()
![]()
Como
![]() onde z
é a distância zenital,
onde z
é a distância zenital,
![]()
Imaginemos a atmosfera como uma camada de altura H, Fo o fluxo no topo da atmosfera e F o que chega ao observador. Então,
![]()
A espessura ótica é uma função da distância zenital z, e supondo que a camada atmosférica é formada por camadas plano-paralelas, ela pode ser expressa por τ=τosec z, onde τo= kH é a espessura ótica na direção do zênite, e o fluxo será:
![]()
Em magnitudes, essa equação fica:
Um exemplo de aplicação deste conceito é considerarmos uma estrela observada a uma distância zenital de 45°. Como sec 45°= 1,41 e usando um coeficiente K = 0,40, típico de observações óticas, obtemos F = 0,57 Fo, ou seja, a atmosfera terrestre absorve 43% da luz da estrela ao observarmos a 45° do zênite.
A diferença (m - mo) é a extinção atmosférica em magnitudes, e é determinada através de estrelas padrões para as quais mo é conhecido.
A constante K é característica do meio, e depende do comprimento de onda, sendo mais correto escrever
![]()
Para o sistema UBV, e para locais situados acima de 2000 m de altitude,
Se observarmos uma estrela a 45° do zênite, vemos que a extinção atmosférica neste caso equivale a 0,48 sec 45°=0,68 mag em U, 0,25 sec 45°=0,35 mag em B e 0,14 sec 45°=0,20 mag em V. A magnitude do Sol cai de -26,7 para cerca de -15,8 no horizonte.
| Distância Zenital | Massa de ar |
|---|---|
| 88° | 19,79 |
| 87° | 15,36 |
| 86° | 12,44 |
| 85° | 10,40 |
| 84° | 8,90 |
| 82° | 6,88 |
| 80° | 5,60 |
| 75° | 3,82 |
| 70° | 2,90 |
| 65° | 2,36 |
| 60° | 2,00 |
| 50° | 1,55 |
| 40° | 1,30 |
| 30° | 1,15 |
| 20° | 1,06 |
| 10° | 1,02 |
| 0° | 1,00 |
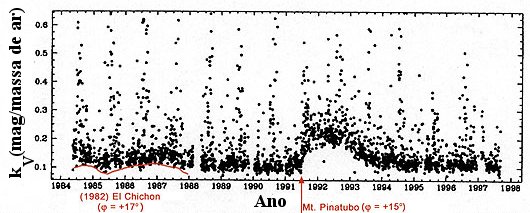
Além da extinção atmosférica, é necessário levar em conta também a extinção interestelar, devida à poeira interestelar concentrada principalmente no plano da Galáxia, e que também extingue a luz das estrelas. A extinção interestelar depende da direção em que se encontra o objeto, visto que a distribuição de matéria na nossa galáxia não é homogênea. A luz provinda de outras galáxias também sofre extinção dentro das próprias galáxias.
Se não existisse extinção, a magnitude visual absoluta MV de uma estrela de magnitude aparente Vo, localizada a uma distância d seria:
|
Considerando que a magnitude aparente V está afetada por avermelhamento, Vo=V-AV, e a magnitude visual absoluta será:
|
Similarmente, a magnitude azul absoluta será:
|
|
|
Vemos assim que, embora a magnitude aparente uma estrela dependa de sua distância, o índice de cor não depende da distância e, por isso, é muito útil para determinar a temperatura da estrela.
A extinção interestelar em magnitudes é representada pela letra A com um subscrito indicando a banda espectral a que se refere, por exemplo, a extinção interestelar na banda B é AB e na banda V é AV.![A_{\lambda_1}-A_{\lambda_2} = 2,5 \{\log\[\frac{F_0\(\lambda_1\)}{F_0\(\lambda_2\)}\] - \log\[\frac{F\(\lambda_1\)}{F\(\lambda_2\)}\]\}](alambda.png)
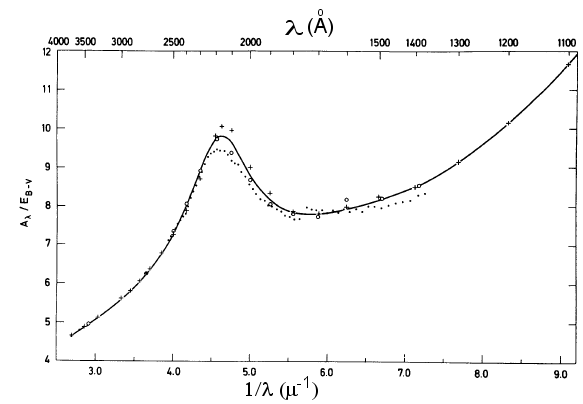
Na ausência de avermelhamento interestelar, as cores (B-V) e (U-B) das estrelas (não da lei de Planck) se encontram em um curva ondulada.
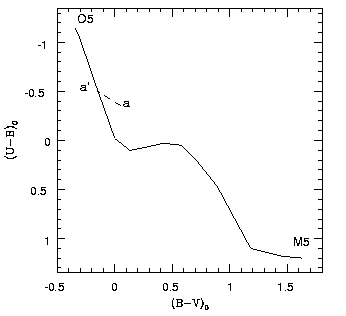
Se a estrela a é encontrada fora desta curva, assumimos que ela sofreu avermelhamento interestelar e movemos a medida para cima ao longo da diagonal de inclinação conhecida
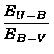 = (0,72 ± 0,03)
= (0,72 ± 0,03)
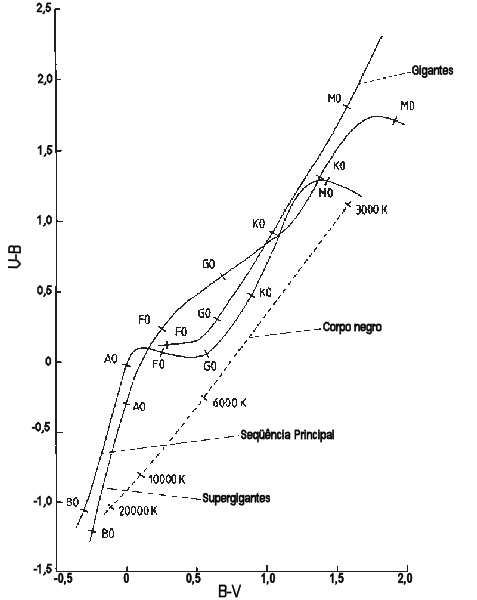
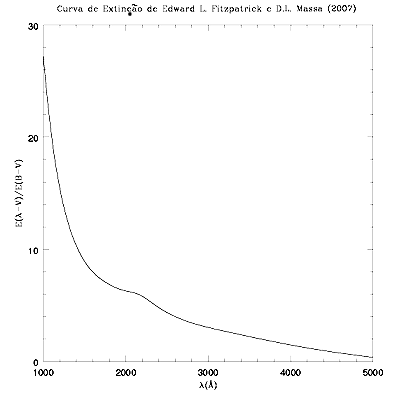
O valor de RV, a razão entre o avermelhamento total e o seletivo, está entre 3,0 e 5,0, dependendo da direção na Galáxia, devido à variação no tamanho e composição química dos grãos de poeira. O valor mais provável, fora das regiões de grande extinção, é de RV=(2,99 ± 0,27), de acôrdo com Edward L. Fitzpatrick & Derck Massa (2007, Astrophysical Journal, 663, 320). A calculadora do NED usa a recalibração do avermelhamento de Edward F. Schlafly & Douglas P. Finkbeiner (2011, Astrophysical Journal, 737, 103, 2011) para as cores do SDSS e recomenda RV=3.1.
Para a magnitude G do satélite Gaia, RG=2.72.
Uma aproximação para a absorção interestelar é Aλ = 6,5×10-10/λ - 2,0×10-4 mag/pc.
Desta maneira podemos obter os valores reais dos fluxos, isto é, os fluxos corrigidos pelo avermelhamento interestelar, e medir não somente a temperatura, mas também estimar a correção bolométrica C.B., que definimos como:
| Tipo | (B - V)0 | (U - B)0 | Tef | C.B. | MBol | Massa
( |
|---|---|---|---|---|---|---|
| O5 | -0,35 | -1,15 | 40000 | 4,00 | -10,0 | 120 |
| B0 | -0,31 | -1,06 | 28000 | 2,80 | -6,8 | 17 |
| B5 | -0,16 | -0,55 | 15500 | 1,50 | -2,6 | 6 |
| A0 | 0,00 | -0,02 | 9900 | 0,40 | 0,1 | 2,9 |
| A5 | 0,13 | 0,10 | 8500 | 0,12 | 1,7 | 2,2 |
| F0 | 0,27 | 0,07 | 7400 | 0,06 | 2,6 | 1,6 |
| F5 | 0,42 | 0,03 | 6580 | 0,00 | 3,4 | 1,25 |
| G0 | 0,58 | 0,05 | 6030 | 0,03 | 4,3 | 1,1 |
| G5 | 0,70 | 0,19 | 5520 | 0,07 | 5,0 | 0,9 |
| K0 | 0,89 | 0,47 | 4900 | 0,19 | 5,8 | 0,8 |
| K5 | 1,18 | 1,10 | 4130 | 0,60 | 6,7 | 0,65 |
| M0 | 1,45 | 1,18 | 3480 | 1,19 | 7,8 | 0,5 |
| M5 | 1,63 | 1,20 | 2800 | 2,30 | 9,8 | 0,15 |
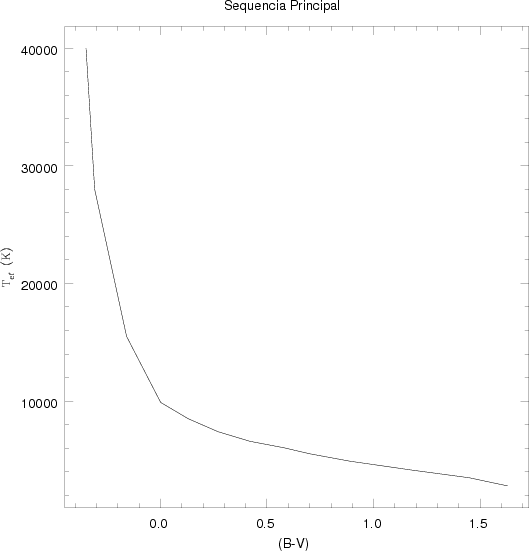
Em 1859-60, os físicos encontraram um problema: como descrever matematicamente como um corpo aquecido irradia energia, isto é, quanto ele emite em cada comprimento de onda. Para abordar o problema, começaram por examinar um caso teórico simplificado, o corpo negro, definido pelo físico alemão Gustav Robert Kirchhoff (1824-1887), na Universidade de Heidelberg, como um objeto que absorve toda a luz que incide sobre ele, sem refletir nada da radiação. Um corpo com essa propriedade, em princípio, não pode ser visto e, portanto, é negro. Para tal corpo estar em equilíbrio termodinâmico, ele deve irradiar energia na mesma taxa em que a absorve, do contrário ele esquentaria ou esfriaria, e sua temperatura variaria. Portanto, um corpo negro, além de ser um absorsor perfeito, é também um emissor perfeito. Desde então muitos experimentos tentaram medir seu espectro, isto é, como sua intensidade varia com a freqüência. Um exemplo é um forno grande com um pequeno furo por onde medimos a radiação.
 Em 1900, o físico alemão Max Karl Ernst Ludwig Planck (1858-1947)
postulou que a energia eletromagnética só pode se
propagar em quanta discretos, ou fótons.
Albert Einstein (1879-1955), em 1905, assumiu que cada fóton tem
energia E=h × freqüência
Em 1900, o físico alemão Max Karl Ernst Ludwig Planck (1858-1947)
postulou que a energia eletromagnética só pode se
propagar em quanta discretos, ou fótons.
Albert Einstein (1879-1955), em 1905, assumiu que cada fóton tem
energia E=h × freqüência
A intensidade específica monocromática,
energia por unidade de comprimento de onda, por
segundo, por unidade de área, e por unidade de ângulo sólido,
de um corpo que tem uma temperatura uniforme T e está em
equilíbrio termodinâmico com seu próprio
campo de radiação - isto é, é opaco -, é chamada
![]() e
é dada pela Lei de Planck:
e
é dada pela Lei de Planck:
![]()
já que E é a energia da partícula - fóton- , que viaja com velocidade c, a velocidade da luz,
se espalha por um ângulo sólido 4π,
e dnb(p) é o número de fótons com momentum p, associado à energia E, e é
dado pela distribuição de momentum
de Bose-Einstein de um gás de bósons de spin s:
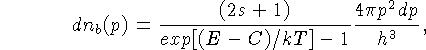
onde C é um multiplicador lagrangeano
(número real) que depende da densidade
de partículas (número de partículas
por unidade de volume N) e é obtido integrando-se:
![]()
O termo (2s+1) representa o número de partículas
(estados independentes) possíveis com mesma energia E,
e o termo h-3 é necessário devido ao Princípio
da Incerteza de Heisenberg,
proposto em 1927 pelo alemão Werner Karl Heisenberg (1901-1976):
Para um fóton, que é um bóson de massa zero e spin 1,
![]() ,
,
![]() ,
,
![]() e C=0,
se obtem:
e C=0,
se obtem:
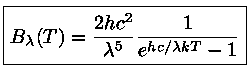
Para escrever a lei de Planck em termos de freqüência, precisamos levar em conta que a mesma energia é emitida em unidades de comprimento de onda ou de frequência:
![]() = -
= -
![]()
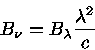
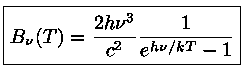
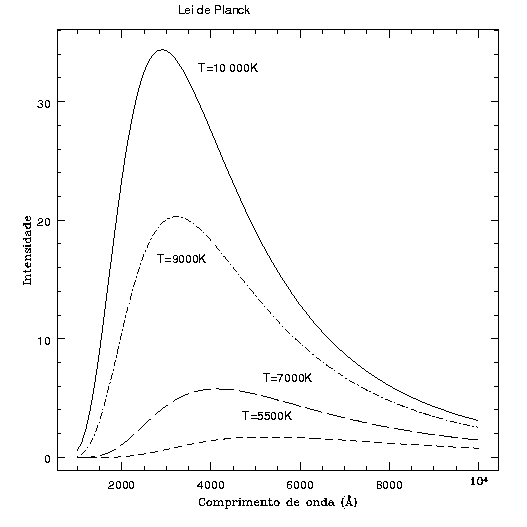
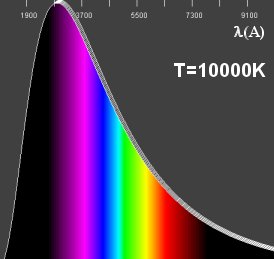
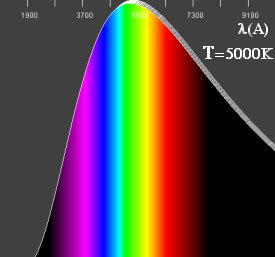
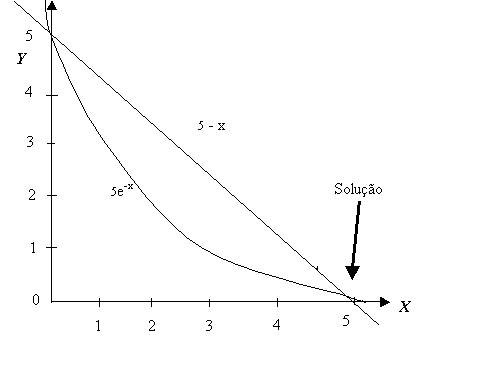
Como podemos ver da figura com a Lei de Planck, o comprimento de onda em que a intensidade é máxima varia com a temperatura.
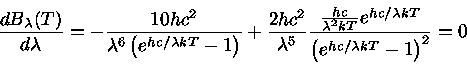
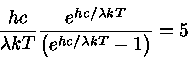
|
|
(1) |
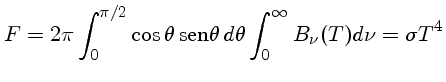
Esse resultado pode ser demonstrado considerando que:
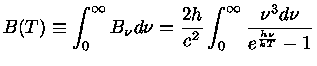
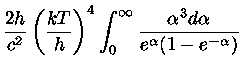 |
|||
![\frac{2h}{c^2}(\frac{kT}{h})^4 [6 \sum_{n=0}^\infty
\frac{1}{(n+1)^4}]](img5111.gif) |
|||
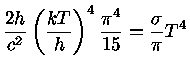 |
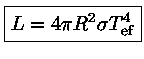
A temperatura efetiva de uma estrela é portanto a temperatura de um corpo negro que emite a mesma quantidade de energia por unidade de área e por unidade de tempo.
A luminosidade do Sol, isto é, a energia total
emitida pelo Sol é ![]() ,
sendo que 1 Joule = 107 ergs.
,
sendo que 1 Joule = 107 ergs.
Como o raio do Sol é de ![]() 700 000 km,
segue
que a temperatura efetiva do Sol é
Tef⊙ = 5400K.
700 000 km,
segue
que a temperatura efetiva do Sol é
Tef⊙ = 5400K.
Usando o fato do Sol emitir o máximo no amarelo, podemos então escrever a equação de Wien (1) aproximadamente como
No modelo de Jorge E. Vernazza, Eugene H. Avrett & Rudolf Loeser, (1973, Astrophysical Journal, 184, 605), a maior parte do espectro visível do Sol tem origem em uma camada com cerca de 1000 km de extensão, e a temperatura varia de 9000K a 4000K. A gravidade superficial do Sol é de g=2,738 × 104cm/s2 = 273,8 m/s2 →[log g=4.44 (c.g.s.)].
A definição de temperatura de um objeto astronômico não é única, pois depende do método que estamos usando para medi-la. Assim, a temperatura de uma estrela medida pela lei de Wien (a partir da intensidade em um comprimento de onda), é ligeiramente diferente da sua temperatura medida pela lei de Stefan-Boltzmann (a partir da luminosidade e do raio). Esta última é chamada temperatura efetiva, enquanto a primeira é chamada temperatura de brilho. Pode-se ainda definir a temperatura de cor, determinada a partir da razão de fluxos em dois comprimentos de onda diferentes. Essas temperaturas não são iguais porque os corpos astronômicos não são corpos negros perfeitos.
A energia vinda do Sol que atinge a Terra por unidade de área e de tempo,
por definição de
fluxo, é de:
![]()
onde r é a distância do Sol à Terra, de 1 unidade astronômica
(UA) = 150 milhões de km,
e ![]() .
.
A secção reta πR⊕2 da Terra, onde
o raio da Terra R⊕=6400 km,
intercepta a potência luminosa
![]()
Devido à rotação e à atmosfera da Terra, o fluxo médio do Sol incidente sobre a Terra é
obtido dividindo a potência interceptada na Terra pela área
total da Terra, 4πR⊕2.
![]()
A Terra absorve 61% da luz incidente, refletindo os outros 39%.
A energia absorvida aquece a Terra, que irradia como
um corpo negro a uma taxa σT⊕4
por unidade de área.
Logo,
![]()
o que resulta em uma temperatura para a Terra de
![]() K.
K.
De fato, devido ao efeito estufa do gás carbônico (CO2) e da água na atmosfera da Terra, a temperatura da Terra é de 290 K=17 C. Portanto o efeito estufa mantém a água na superfície da Terra acima do ponto de congelamento, de 273 K.
A escala de temperatura que usamos quotidianamente é a Celsius [Anders Celsius (1701-1744)], cuja divisão é também chamada de graus centígrados, pois varia de 1 a 100 do ponto de congelamento até a ebulição da água. A relação entre os dois sistema é: T(C)=T(K)-273, ou seja, 0 C=273 K. O zero absoluto de temperatura, onde todas as partículas estariam paradas, 0 K=-273,16 C, foi estabelecido teoricamente em 1848 pelo engenheiro e físico irlandês William Thomson (1824-1907), o Lord Kelvin, em seu artigo On an Absolute Thermometric Scale, no Philosophical Magazine.
Esse caso, que ocorre na atmosfera de uma estrela, é chamado equilíbrio termodinâmico local. É um conceito importante na teoria de interiores de estrelas e evolução estelar.
As camadas mais internas das estrelas são mais quentes e emitem mais radiação que as camadas mais externas. Assim, a luz (ou melhor, a radiação, pois a maior parte não é visível), sai de uma camada quente mais interna [chamemos de camada (n-1)], passa pela camada considerada (n) e atinge uma camada FRIA mais externa (n+1). Para haver equilíbrio, isto é, para a temperatura se manter, será necessário que a energia que entra, vinda da camada (n-1), seja transmitida para a camada (n+1), sem ficar "depositada" na camada n e aumentar sua temperatura. Isso, porém, não significa que a camada n é transparente, mas que a radiação vai fluir do interior da estrela para fora. Aliás, no interior da estrela, a radiação vai se deslocar somente uns poucos centímetros antes de ser reabsorvida. Mas depois ela será re-emitida em todas as direções e vai fazer um caminho em zig-zag lentamente até a superficie da estrela.
Assim, o resultado final é que a energia gerada nas reações nucleares no núcleo da estrela vai acabar sendo emitida na superfície da estrela, passando pelas camadas intermediárias sem alterar significativamente a distribuição de temperatura dessas camadas. Isso é bem diferente do equilíbrio termodinâmico per se, em que as todas as camadas têm a mesma temperatura.
O espectro emitido no centro da estrela, pelas reações nucleares, é "duro", de raios gama, mas logo vai ser "abrandado" ou ficar mais "mole" - de comprimento de onda maior e energia menor por "fóton". Como a energia total se mantem e cada fóton tem menos energia, o número de fótons é muito maior. Nesse processo, que envolve um enorme número de eventos ou colisões entre os fótons e a matéria, o espectro será contínuo, distribuído em todas as freqüências. Ao migrar para camadas mais externas e frias, o espectro se torna cada vez mais "mole", passando a ser principalmente em raios X, ultravioleta e, finalmente, perto da superfície, no vísivel.
A "superfície" de uma estrela - fotosfera - não é uma camada de propriedades químicas e físicas distintas, como nos planetas. Toda a estrela é um gás, que absorve e reemite a radiação, de acordo com a sua temperatura. Mais no centro, o gás (na maioria hidrogênio e hélio) está todo ionizado, sendo composto de núcleos e elétrons livres. Porém a temperatura é menor na superfície, havendo átomos que podem ter elétrons em diferentes energias. Mas os elétrons de um átomo não podem ficar em qualquer nível de energia - é um fato básico e muito intrigante da mecânica quântica. Eles só "podem aceitar" energia de comprimento de onda bem determinado (6563 Å, da linha Hα, por exemplo, no átomo de H) e então "pulam" para um nível mais alto, absorvendo o fóton dessa energia. Não podem absorver os fótons de menos energia, nem tampouco os de mais energia, a não ser de energia bem maior, que permite "pular" dois níveis para cima. Assim, quando a radiação passa pela camada externa - menos densa e mais fria - os átomos dessa camada vão absorver apenas os fótons de comprimentos de onda característicos, que serão removidos da radiação que se desloca da camada mais interna para fora da estrela. Além da fotosfera, o gás está tão rarefeito que, na prática, não mais absorve a radiação visível. Assim, a "superfície" é apenas um fenômeno ótico, relacionado com a emissão e absorção da luz da estrela.
Portanto, superpostas na radiação contínua emitida pela estrela, aparecem linhas escuras - linhas de Fraunhofer, que as identificou, classificou e estudou a partir de 1814 -, características dos elementos químicos das camadas superficiais da estrela. Porém, o gás que absorve a luz também se aquece. Na fotosfera do Sol, a temperatura é superior a 5000 K. As linhas escuras nunca são totalmente escuras ou desprovidas de luz. Elas têm a contribuição da luz emitida pelo gás que absorve a luz, mas que também a reemite.
O sistema de medidas de som em decibéis também é uma escala logarítmica, com 20 db correspondendo a um fator de 100.
Em fevereiro de 2015, a União Astronômica Internacional recomenda: Mbol=0 para LSol=3,012×1028 W de modo que no sistema métrico, com luminosidade em Watts,
Mbol = -2,5 log(L/LSol) = 2,5 log L + 71,1971374188
que corresponde a MSol=4,74.
Desta definição, a magnitude aparente mbol=0 corresponde a fluxo fSol=2,51735238314×10-8 W m-2 e
mbol = -2,5 log(f/fSol) = -2,5 log f - 18,9976399673
![]() Espectroscopia
Espectroscopia
![]() Astronomia e Astrofísica
Astronomia e Astrofísica
![]()
©