Polarização

A luz pode ser polarizada por:

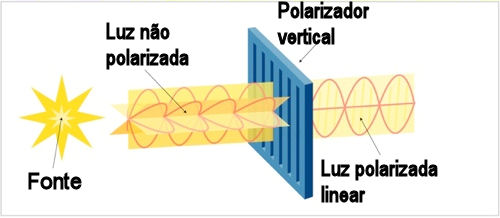
emissão ciclotron (campo elétrico com uma frequência alta e constante e um campo magnético perpendicular estático) ou síncroton (campo magnético variável) - partíticulas carregadas aceleradas por um campo magnético, produzindo polarização linear de até 45% em blazares. O ângulo de polarização é perpendicular ao campo magnético local.
absorção dicróica, em que grãos de poeira alinhados com um campo magnético absorvem um estado de polarização e transmitem o estado ortogonal. Quando a radiação passa por uma nuvem ela torna-se polarizada com o vetor E paralelo ao campo magnético.
espalhamento por elétrons ou poeira, gerando polarização linear perpendicular ao plano de espalhamento, ou circular por múltiplos espalhamentos.
campos magnéticos estelares

O astrônomo francês Dominique François Jean Arago (1786-1853) descobriu que a luz da Lua era polarizada em 1811 e durante o eclipse de 1842 ele examinou a luz polarizada da coroa e cromosfera do Sol, determinando que o limbo do Sol é gasoso. Em 1908, George Ellery Hale (1868-1938) descobriu que a luz das manchas solares é polarizada tanto linearmente quanto circularmente. O astrônomo francês Bernard Ferdinand Lyot (1897-1952) realizou seu doutorado em 1929 no estudo da luz polarizada pela reflexão na superfície dos planetas. Em 1946, Horace Welcome Babcock (1912-2003) usou polarimetria para demonstrar que a estrela 78 Virginis também tinha campo magnético.

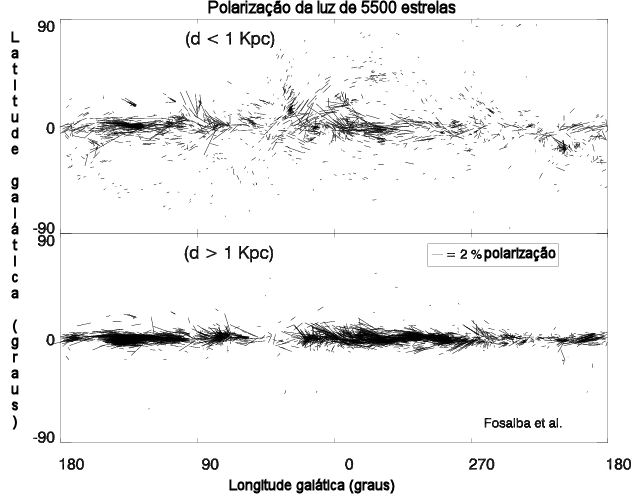
Se há uma orientação particular para os átomos emissores, como um gás em um campo magnético, há polarização da luz emitida. Muitas emissões de rádio envolvem campos magnéticos, de modo que muitas fontes de rádio mostram forte polarização.

A polarização da luz das estrelas, de cerca de 1%, foi descoberta independentemente por John Scoville Hall (1908-1991) (1949, Science, 109, 166) e William Albert Hiltner (1914-1991) (1949, Science, 109, 65). No mesmo ano Leverett G. Davis Junior (1914-2003) e Jesse Leonard Greenstein (1909-2002) explicaram no artigo The Polarization of Starlight by Interstellar Dust Particles in a Galactic Magnetic Field, Physical Review, 75, 1605 que ela era causada pela orientação dos grãos de poeira do meio interestelar com o campo magnético. A distribuição da polarização foi usada para mapear o campo magnético da Via Láctea por Krzysztof Serkowski, Don S. Matthewson e Vince L. Ford (1975, Astrophysical Journal 196, 261) e em 2002 por Pablo Fosalba, Alex Lazarian, Simon Prunet e Jan A. Tauber (Astrophysical Journal, 564, 762).

A polarização da luz se dá quando a distribuição dos vetores elétricos dos fótons em um feixe não é randômica. Normalmente distingüimos dois tipos de polarização: linear e circular. Na linear, os vetores elétricos são todos paralelos e com direção constante. Na circular, o ângulo do vetor elétrico gira com o tempo, na freqüência da radiação. Todos os tipos de radiação podem ser descritos como diferentes aspectos de radiação parcialmente polarizada elipticamente.

As propriedades de luz parcialmente elipticamente polarizada são completamente descritas pelos quatro parâmetros de Stokes [Sir George Gabriel Stokes (1819-1903), em 1852]:

intensidade da luz não polarizada,
grau de elipticidade,
direção do eixo maior da elipse e
sentido de rotação da luz polarizada.

Parâmetros de Stokes

O vetor de Stokes (I,Q,U,V) descreve qualquer caso:

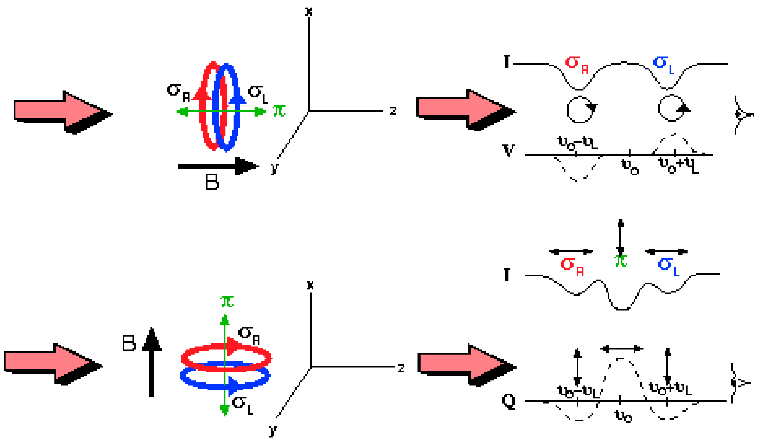
(1,0,0,0) = luz não polarizada
(1,1,0,0) = luz 100% polarizada linearmente em 0° (Norte-Sul)
(1,0,1,0) = luz 100% polarizada linearmente em 45°
(1,-1,0,0) = luz 100% polarizada linearmente a 90° (Leste-Oeste)
(1,0,0,1) = luz 100% polarizada circularmente

Se considerarmos que a radiação está se propagando ao longo do eixo z de um sistema de coordenadas tri-dimensional retangular, então a componente polarizada do vetor elétrico pode ser descrita como:

$E_x(t) = e_1 \cos(2\pi \nu t)$

$E_y(t) = e_2 \cos(2\pi \nu t + \delta)$

onde $\nu$ é a freqüência da radiação, $\delta$ é a diferença de fase entre as componentes x e y, e

são as amplitudes das componentes x e y.

Os parâmetros de Stokes I, Q, U e V são então dados por

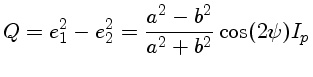
$Q = e_1^2 - e_2^2 = \frac{a^2 - b^2}{a^2 + b^2} \cos(2\psi) I_p$

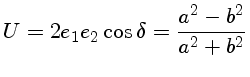$U = 2e_1e_2 \cos \delta = \frac{a^2 - b^2}{a^2 + b^2}$ sen $(2\psi) I_p$

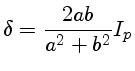
sen $\delta = \frac{2ab}{a^2 + b^2} I_p$

onde

é a intensidade da luz polarizada,

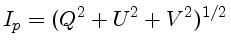
$I_p = ( Q^2 + U^2 + V^2)^{1/2}$

e I é a intensidade total da luz parcialmente polarizada,

onde

é a intensidade da luz não polarizada, e

$a=\Big(\frac{e_1^2 + e_2^2}{1+\tan^2[\frac{1}{2}\mathrm{sen}^{-1} (\frac{2e_1e_2}{e_1^2 + e_2^2}\mathrm{sen}\delta)]}\Big)^{1/2}$

$b=a\tan\Big[\frac{1}{3}\mathrm{sen}^{-1}\big(\frac{2e_1e_2}{e_1^2 + e_2^2}\mathrm{sen}\delta\big)\Big]$

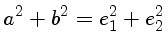
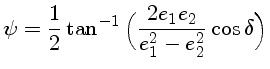
$\psi=\frac{1}{2}\tan^{-1}\Big(\frac{2e_1e_2}{e_1^2 - e_2^2}\cos\delta\Big)$

O grau de polarização, $\pi$ , da radiação é dado por

$\pi=\frac{( Q^2 + U^2 + V^2)^{1/2}}{I}=\frac{I_p}{I}$

enquanto que o grau de polarização linear, $\pi_L$ , e de polarização elíptica, $\pi_e$ , são:

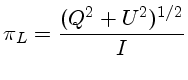
$\pi_L = \frac{(Q^2 + U^2)^{1/2}}{I}$

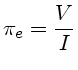
$\pi_e = \frac{V}{I}$

Quando V=0, isto é, a diferença de fase, $\delta$ , é nula ou , a radiação está linearmente polarizada. O grau de polarização será então igual ao grau de polarização linear, e dado pela quantidade comumente determinada experimentalmente,

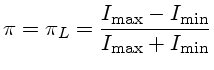
$\pi = \pi_L = \frac{I_\mathrm{max}-I_\mathrm{min}}{I_\mathrm{max}+I_\mathrm{min}}$

onde $I_\mathrm{max}$ e $I_\mathrm{min}$ são as intensidades máximas e mínimas observadas quando o polarizador gira. O valor de $\pi_e$ é positivo para radiação polarizada para a direita (anti-horário) e negativo para polarização para a esquerda (horário).

Um polarímetro é um instrumento que mede o estado da polarização, idealmente os valores dos quatro parâmetros de Stokes, e sua variação com tempo, espaço e comprimento de onda. Os de feixe duplo medem simultaneamente duas componentes, usando um prisma de Wollaston, composto de dois prismas de calcita (CaCO₃, com índices de refração n_o=1,658 e n_e=1,486 em 5900 Å) com eixos óticos perpendiculares, que separa a luz polarizada em duas componentes ortogonais

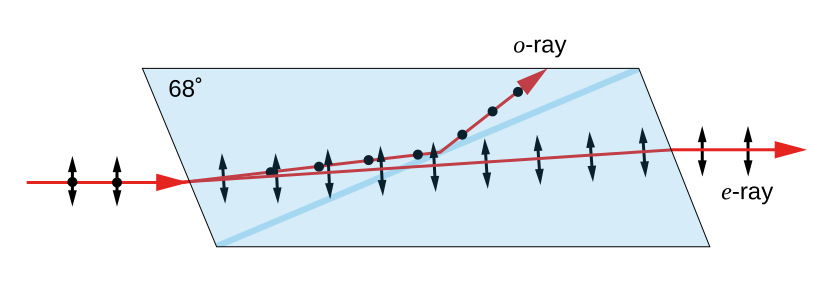
e uma placa retardadora de meia onda - a onda paralela ao eixo ótico do cristal birefringente se propaga um pouco mais devagar que a perpendicular, chegando ao final da placa retardada de meio comprimento de onda, para alternar entre os dois feixes. Escolhendo apropriadamente a espessura do cristal, o comprimento de onda da luz e a variação do índice de refração do material, introduz-se a mudança de fase desejada entre as duas componentes de polarização. Em 1802, o médico, químico e físico inglês William Hyde Wollaston (1766-1828) observou que, passando a luz solar por uma fenda e depois por um prisma, apareciam algumas linhas escuras no espectro, que ele interpretou erroneamente como o limite das cores A method of examining refractive and dispersive powers, by prismatic reflection, Philosophical Transactions of the Royal Society, 92: 365-380). Ele desenvolveu um método para separar a platina do minério, e descobriu o paládio em 1802 e o ródio em 1804, e inventou o prisma de Wollaston, com dois prismas de calcita ortogonais, que separam a luz polarizada em dois feixes com polarizações ortogonais.

Prisma de Wollaston e Placa Retardadora do polarímetro do FORS do ESO.

O imageador e espectrógrafo FORS2 (FOcal Reducer and low dispersion Spectrograph) do telescópio de 8,4 m VLT (Very Large Telescope) no ESO (European Southern Observatory), no Chile, pode medir a polarização linear, usando um retardador λ/2 ou a circularmente polarizada, passando a luz por uma retardador λ/4. O resultado é que saem dois feixes linearmente polarizados com a mesma direção e superpostos, que entram numa calcita e se dividem em dois feixes, um é ordinário - mais lento (v_o=c/n_o), e o outro, extraordinário - mais rápido [v_e=c/n_e, n_e < n_o, como na calcita (cristais de CaCO₃)] que são medidos pelo mesmo CCD. O espectro final é composto destes dois espectros. Ao subtrair um espectro do outro, se houver polarização, vai ficar uma emissão e uma absorção em relação à média. A distância entre a emissão e a absorção, em comprimento de onda, mede o Δλ das componentes Zeeman.

Para medidas de polarização é necessário reduzir a polarização instrumental, causada principalmente por reflexões em planos inclinados, ou no detector. Deste modo, telescópios Newtonianos e coudés não podem ser usados para medir polarização por causa de seus espelhos inclinados.

Os parâmetros de Stokes normalizados são medidos usando-se diferentes ângulos do polarizador:

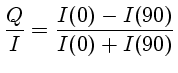
$\frac{Q}{I} = \frac{I(0)-I(90)}{I(0)+I(90)}$

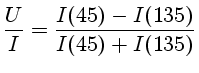
$\frac{U}{I} = \frac{I(45)-I(135)}{I(45)+I(135)}$

$I = I(\theta)+I(\theta+90^o)$

O efeito da polarização em um perfil de linha espectral $I(\lambda)$ é determinado pela componente na linha de visada do campo magnetico efetivo, , na região de formação de linhas, e pela inclinação do espectro, $dI/d\lambda$ . A separação Zeeman das linhas em componentes com polarização oposta resulta em uma polarização circular medida pelo parâmetro de Stokes

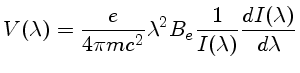
$V(\lambda) = \frac{e}{4\pi m c^2} \lambda^2 B_e \frac{1}{I(\lambda)} \frac{dI(\lambda)}{d\lambda}$

se $V\ll 1$ , ou seja, para campos da ordem de kG. Para campos maiores a polarização do contínuo é importante.

Ferdinando Patat e Martino Romaniello publicaram o artigo Error Analysis for Dual-Beam Optical Linear Polarimetry, no 2006, Publications of the Astronomical Society of the Pacific, 118, 146. Stefano Bagnulo, John D. Landstreet, L. Fossati & O. Kochukhov, no artigo de 2012 no Astronomy & Astrophysics, 538, 129, estudam a polarização instrumental e criticam os valores de polarimetria medidos com o FORS até então.

No 3,6 m CFHT - Canada-France-Hawaii Telescope, o espectropolarímetro echelle ESPaDOnS pode medir polarimetria para estrelas mais brilhantes que V=15.

Neutrinos

Próxima:Astrometria Volta: Telescópios Anterior: Rádio Telescópios

Astronomia e Astrofísica