

Próxima: Cosmologia na Relatividade Geral
Volta: Cosmologia Relativística
Anterior: Relatividade Geral
Da mesma forma que os componentes de um vetor mudam quando mudamos a base do espaço vetorial, os componentes de um tensor também mudam sob transformações de base.
Os índices de um tensor, superiores (contravariante) ou inferiores (covariantes) descrevem
como ele se transforma com uma mudança de base.
Se um índice de um tensor
se transforma como um vetor com o inverso da transformação de base
(por exemplo, a posição e a velocidade variam de forma oposta ao da nova base) ele é dito contravariante
e é denotado com um índice superior.
Um índice que se transforma com a transformação própria base é chamado covariante e é indicado com um índice inferior.
Nas equações acima, algumas vezes aparece
a componente covariante de Lorentz 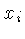 e outras
vezes a componente contravariante
e outras
vezes a componente contravariante 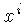 .
A relação entre elas é:
.
A relação entre elas é:
sendo que
e


Próxima: Cosmologia na Relatividade Geral
Volta: Cosmologia Relativística
Anterior: Relatividade Geral
©
Modificada em 10 dez 2012
![]() e outras
vezes a componente contravariante
e outras
vezes a componente contravariante ![]() .
A relação entre elas é:
.
A relação entre elas é: