Consideremos agora a força gravitacional resultante sobre uma
partícula pertencente a um Universo de massa ![]() , homogêneo
e isotrópico, em expansão.
Consideraremos uma
partícula na superfície da esfera de raio
, homogêneo
e isotrópico, em expansão.
Consideraremos uma
partícula na superfície da esfera de raio ![]() :
:
Em um dado instante, a partícula sofrerá uma aceleração gravitacional dada por:
A energia mecânica da partícula,
![]() ,
assumindo-se a constante cosmológica
,
assumindo-se a constante cosmológica
![]() =0,
será:
=0,
será:
Note que no caso em que apenas a gravidade atua no Universo,
![]() .
Neste caso, sabemos que o sinal de
.
Neste caso, sabemos que o sinal de
![]() determina se as
partículas poderão se afastar indefinidamente umas das outras ou não:
determina se as
partículas poderão se afastar indefinidamente umas das outras ou não:
![]() expansão indefinida: Universo aberto.
expansão indefinida: Universo aberto.
![]() expansão contida: Universo fechado.
expansão contida: Universo fechado.
Omitiremos a coordenada ![]() para r(t) e H(t) na derivação a seguir.
Como a massa
para r(t) e H(t) na derivação a seguir.
Como a massa ![]() é dada por
é dada por
Seja agora a densidade crítica, ![]() ,
definida como aquela para a qual a gravidade
está no limite de conter a expansão (ou seja,
,
definida como aquela para a qual a gravidade
está no limite de conter a expansão (ou seja, ![]() ):
):
Inserindo ![]() na eq. (9), temos:
na eq. (9), temos:
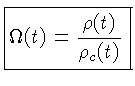
Como ![]() e
e ![]() são sempre positivos,
os sinais de
são sempre positivos,
os sinais de ![]() e
e ![]() estão anti-correlacionados:
estão anti-correlacionados:
![]() : Universo fechado.
: Universo fechado.
![]() :
Universo aberto.
:
Universo aberto.
![]() :
Universo plano.
:
Universo plano.
Vamos escrever a energia ![]() em termos das propriedades no presente,
usando-se a lei de Hubble:
em termos das propriedades no presente,
usando-se a lei de Hubble:
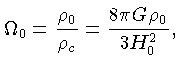
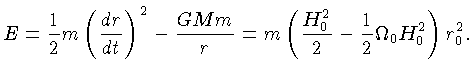
![$\displaystyle \frac{\dot{r}^2}{r_0^2}-\frac{2G}{r}\frac{4\pi}{3}\frac{r_0^3}{r_0^2}\rho_0
=H_0^2\left[1-\Omega_0\right],$](img63.gif)
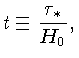
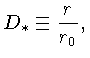
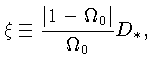
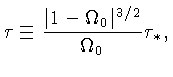
A solução da equação (14) pode ser obtida de:
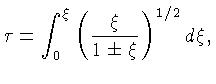
A solução,
para o caso do denominador ![]() ,
em que o Universo é fechado e
,
em que o Universo é fechado e
![]() ,
pode ser encontrada fazendo-se a substituição
,
pode ser encontrada fazendo-se a substituição
![]() , pois obtemos a identidade trigonométrica
, pois obtemos a identidade trigonométrica
![]() .
Para o caso do denominador
.
Para o caso do denominador ![]() ,
em que o Universo é aberto e
,
em que o Universo é aberto e ![]() ,
a substituição é
,
a substituição é
 , pois obtemos a identidade trigonométrica
, pois obtemos a identidade trigonométrica
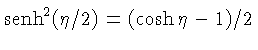 .
Por definição:
.
Por definição:
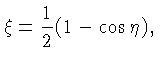 |
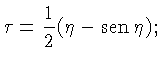 |
Substituindo as definições de ![]() e
e ![]() , obtemos:
, obtemos:
Para
![]() :
:
Para simplificar as equações, vamos definir a variável ![]() :
:
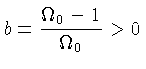
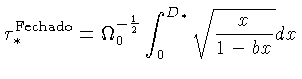
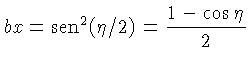
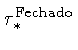 |
 |
||
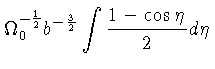 |
|||
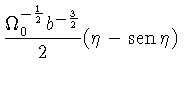 |
|||
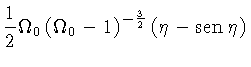 |
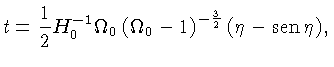 |
(1.17) |
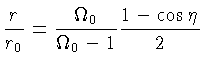 |
(1.18) |
Para ![]() ,
, ![]() :
:
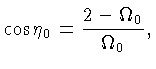 |
Para
![]() ,
,
![]() e
e
![]() :
:
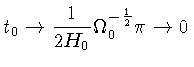
Para
![]() ,
,
![]() e
e
![]() :
:
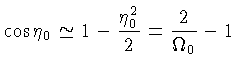
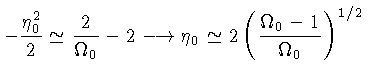
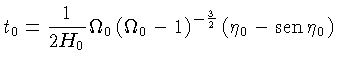
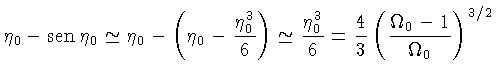
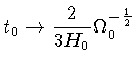
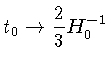
Para ![]() :
:
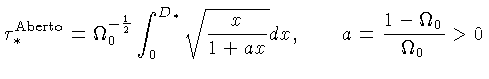
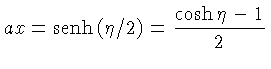
 |
 |
||
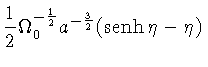 |
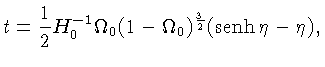 |
(1.19) |
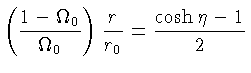
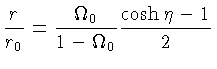
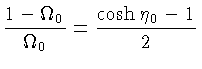
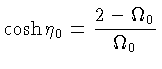
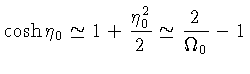
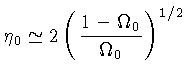
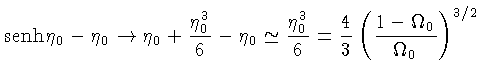
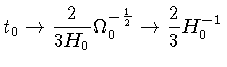
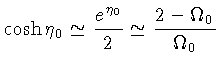
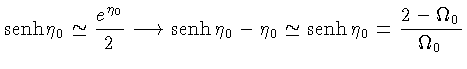
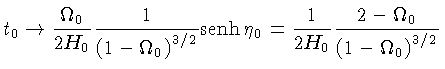
Ou seja, os limites são:
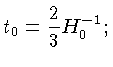 |
Deste modo, a relação entre a idade do Universo e a constante de Hubble no presente, torna-se:
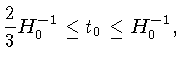 Universo aberto,
Universo aberto,
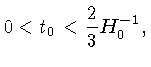 Universo fechado.
Universo fechado.